Zrychlení gravitace: objev, příčiny, vzorec
Zrychlení volného pádu je jedním z mnoha objevů velkého Newtona, který nejen shrnul zkušenosti svých předchůdců, ale také dal přísné matematické vysvětlení velkého množství faktů a experimentálních dat.
Předpoklady pro objevení. Galilejské experimenty
Jeden z mnoha experimentů Galileo Galilei byl věnován studiu pohybu těl v letu. Předtím v systému světového pohledu převažoval názor, že lehčí těla klesají pomaleji než těžké těla. Házení různých objektů z výšky Šikmá věž, Galileo zjistil, že zrychlení volného pádu u těles s různou hmotností je přesně stejné. 
Galileo správně připisoval nepatrné rozdíly mezi teorií a experimentálními daty na vliv odporu vzduchu. Aby dokázal své odůvodnění, navrhl, aby experiment opakoval ve vakuu, ale v té době neexistovala žádná technická možnost. Pouze o mnoho let později udělal myšlenkový experiment Galileo Isaac Newton.
Newtonova teorie
Cti objevu zákon světa patří Newtonovi, ale myšlenka sama byla ve vzduchu asi 200 let. Hlavním předpokladem pro formování nových principů nebeské mechaniky se staly Keplerovy zákony, které formuloval na základě mnoha let pozorování. Z oceánu předpokladů a předpokladů Newton získal předpoklad o síle gravitace Slunce a rozšířil svou teorii na koncept světové rozšíření. Otestoval svou hypotézu o inverzní proporcionalitě síly na čtverec vzdálenosti, když uvažoval o oběžné dráze Měsíce. Následné testy této myšlenky byly provedeny pomocí studie pohybu družic Jupitera. Výsledky pozorování ukázaly, že stejné síly působí mezi satelity planet a samotnými planetami, jako ve vzájemném působení Slunce a planet. 
Objevování gravitační složky
Síla gravitace Země na Slunce dodržovala vzorec:
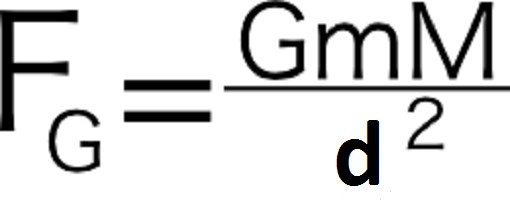
Experimenty ukázaly, že faktor 1 / d2 v tomto vztahu byl zcela aplikovatelný v případě zvažování jiných planet v sluneční soustavě. Konstanta G byla koeficient, který přinesl hodnotu poměru k číselné hodnotě.
Na základě vlastní teorie Newton změřil hmotnostní poměry různých nebeských těles, jako je Jupiterova masová hmotnost / hmotnost Slunce, Měsícová masová hmotnost / Země, ale Newton nemohl dát číselnou odpověď na otázku, kolik Země váží, protože stále zůstává G neznámé.
Velikost gravitační konstanta byl objeven jen půl století po smrti Newtona. Odhady této hodnoty založené na hypotézách, podobné Newtonovým předpokladům, ukázaly, že tato hodnota je zanedbatelná a je téměř nemožné vypočítat její hodnotu za suchozemských podmínek. Běžný gravitace Zdá se to obrovské, protože všechny známé předměty jsou neuvěřitelně malé ve srovnání s hmotností zeměkoule.
Koncem 18. století. G měření
První pokusy o měření G se konaly na konci 18. století. Jako tažná síla použili obrovskou horu. Odhady zrychlení volného pádu byly provedeny na základě odchylky od vertikální hmotnosti kyvadla, umístěné v bezprostřední blízkosti hory. Pomocí geologických dat byla odhadnuta hmotnost hory a její průměrná vzdálenost od kyvadla. Takže jsme dostali první, spíše drsný rozměr tajemné konstanty.
Lord Cavendish Rozměry
Lord Cavendish ve své laboratoři provedl měření gravitační přitažlivosti metodou volného vážení. 
Pro experimenty byla použita kovová koule a masivní kus kovu. Cavendish přiložil malé kovové koule na tenkou prkno a přinesl jim velké olověné koule. V důsledku nárazu se prkna zkroucila, dokud neúspěšný účinek kompenzoval síly Hooke. Experiment byl tak jemný, že dokonce i nejmenší dech vítr mohl zničit výsledky výzkumu. Aby se Cavendish vyhnul konvektinaci, umístil všechna měřicí zařízení do velké krabice, pak ji dal do uzavřené místnosti a sledoval experiment pomocí dalekohledu.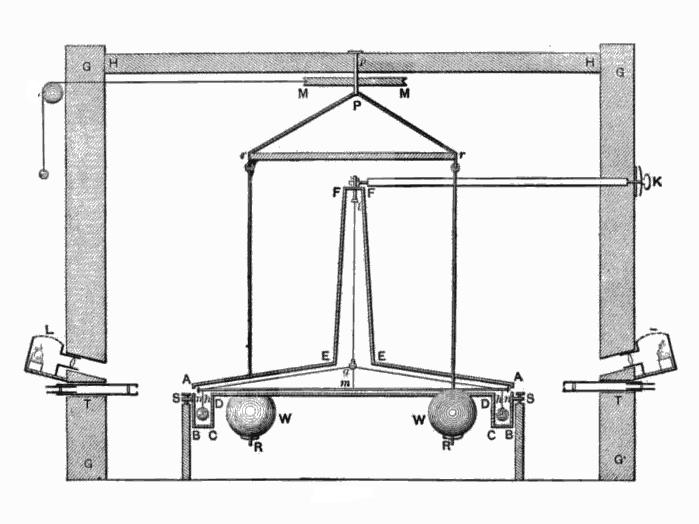 
Po výpočtu síly zkroucení nitě odhadl Cavendish hodnotu G, která byla následně jen nepatrně upravena díky jiným přesnějším experimentům. V moderním systému jednotek:
G = 6,67384 x 10 -11 m 3 kg -1 s -2 .
Tato hodnota je jedna z mála fyzikálních konstant. Jeho hodnota je neměnná v každém bodě Vesmíru.
Měření zrychlení země
Podle Newtonova třetího zákona síla přitažlivosti dvou těl závisí pouze na jejich hmotnosti a vzdálenosti mezi nimi. Tím, že v pravé části rovnice nahrazujeme multiplikátor známý z druhého zákona Newtona, získáváme:
ma = G (mM) / d2.
V našem případě může být hmotnost m snížena a množství a je zrychlení, kterým je tělo m přitahováno ke Zemi. V současné době je zrychlení gravitace obvykle označováno písmenem g. Máme:
g = GM / d2.
V našem případě d je poloměr Země, M je její hmotnost a G je nejvíce nepolapitelná konstanta, kterou fyzici hledají po mnoho let. Nahrazením známých dat do rovnice získáme: g = 9,8 m / s 2 . Tato hodnota je zrychlení volného pádu na Zemi. 
Hodnoty G pro různé zeměpisné šířky
Vzhledem k tomu, že naše planeta nemá tvar koule, ale je to geoid, její poloměr není vždy stejný. Země je zploštělá, takže akcelerace volného pádu přijde na různých hodnotách na rovníku a na obou pólech. Obecně platí, že rozdíl mezi čtením délky poloměru je přibližně 43 km. Proto ve fyzice, při řešení problémů, se urychluje gravitační změna, která se měří na 45 °. Poměrně často k usnadnění výpočtů se předpokládá, že je 10 m / s 2 .
Hodnota G pro měsíc
Naši satelity se řídí stejnými zákony jako ostatní planety v sluneční soustavě. Přesně řečeno, při výpočtu akcelerace na povrchu Měsíce je třeba také vzít v úvahu přitažlivost od Slunce. 
Jak je však zřejmé z vzorce, s rostoucí vzdáleností se hodnota síly přitažlivosti prudce snižuje. Proto odmítněte všechny sekundární síly, použijte stejný vzorec:
G L = GM / d2.
Zde M je hmotnost měsíce a d je jeho průměr. Nahrazením známých hodnot získáme hodnotu G L = 1 622 m / s 2 . Tato hodnota je zrychlení volného pádu na Měsíci.
Je to tak malá hodnota G L, což je hlavní důvod pro nepřítomnost atmosféry na Měsíci. Podle některých informací, v časovém rozmezí, náš satelit měl atmosféru, ale kvůli slabé přitažlivosti Měsíc rychle ztratil. Všechny planety s velkou hmotností mají obvykle svou vlastní atmosféru. Zrychlení volného pádu je dostatečně velké, aby nejen neztratili svou vlastní atmosféru, ale také vzali nějaké množství molekulárního plynu z vesmíru.
Shrňme některé výsledky. Zrychlení z důvodu gravitace je množství, které má každé tělesné tělo. Bez ohledu na to, jak to překvapuje, zní, ale vše, co má maso, přitahuje okolní předměty k sobě. Je to jen to, že tato přitažlivost je tak malá, že v každodenním životě nezáleží. Přesto vědci vážně zvažují i ty nejmenší fyzické konstanty, protože jejich dopad na svět kolem nás není plně pochopen.