Všechny možnosti, jak najít trapézovou oblast
Mnohostranný lichoběžník ... Může být libovolný, rovnoramenný nebo obdélníkový. A v každém případě musíte vědět, jak najít oblast lichoběžníku. Samozřejmě, nejjednodušší způsob, jak si pamatovat základní vzorce. Někdy je ale jednodušší použít ten, který je odvozen ze všech vlastností konkrétního geometrický tvar.
Několik slov o lichoběžníku a jeho prvcích
Jakýkoli čtyřúhelník, jehož dvě strany jsou paralelní, může být nazýván lichoběžníkem. Obecně platí, že nejsou stejné a jsou nazývány základy. Větší z nich je nižší a druhé je horní.
Ostatní dvě strany jsou boční. Pro libovolný lichoběžník mají různé délky. Jsou-li rovny, pak se toto číslo stává rovnoměrné.
Pokud náhle je úhel mezi stranou a základnou 90 stupňů, pak je lichoběžník pravoúhlý.
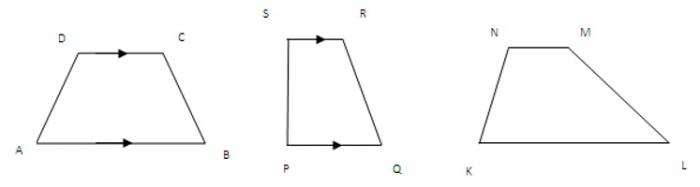
Všechny tyto funkce mohou pomoci při řešení problému, jak najít oblast lichoběžníku.
Mezi prvky tohoto čísla, které mohou být při řešení problémů nepostradatelné, můžeme vyzdvihnout následující:
- výška, tj. segment kolmý k oběma základům;
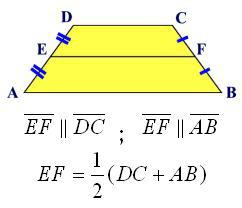
- střední čára, která má se svými konce středové strany.
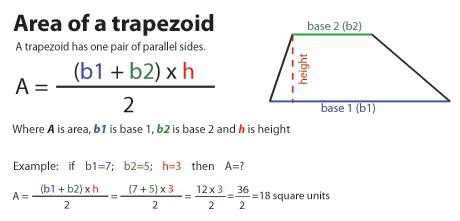
Jaký vzorec pro výpočet plochy, pokud znáte základnu a výšku?
Tento výraz je dán příkazcem, protože nejčastěji tyto hodnoty poznáte, i když nejsou výslovně uvedeny. Takže, abyste pochopili, jak najít trapézní oblast budete muset skládat obě základny a rozdělit je na dvě. Výsledná hodnota se pak vynásobí hodnotou výšky.
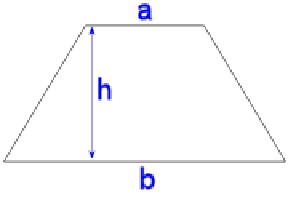
Pokud budeme označovat základy písmeny a 1 a 2 , výška je n, pak vzorec pro oblast bude vypadat takto:
S = ((a 1 + a 2 ) / 2) * n.
Vzorec pro výpočet plochy, pokud je daná jeho výška a střední čára
Pokud se podíváte pozorně na předchozí vzorec, je snadné vidět, že v ní je jasně viditelná hodnota střední čáry. Konkrétně součet základů dělených dvěma. Nechte střední řádek označit písmenem l, pak vzorec pro oblast bude takto:
S = l * n.
Schopnost najít oblast diagonálně
Tato metoda vám pomůže, pokud znáte úhel, který tvoří. Předpokládejme, že diagonály jsou označeny písmeny q 1 a g 2 a úhly mezi nimi jsou α a β. Potom bude vzorec pro nalezení oblasti lichoběžníku zapsán následovně:
S = ((d 1 * d 2 ) / 2) sin sin.
V tomto výrazu můžete snadno nahradit α s β. Výsledek se nezmění.
Jak zjistit oblast, jsou-li známy všechny strany postavy?
Existují také situace, kdy jsou na tomto obrázku známy přesně strany. Tento vzorec je těžkopádný a obtížně zapamatovatelný. Ale je to možné. Nechť strany mají označení: v 1 a 2 , základna a 1 více než 2 . Pak oblast vzorec bude vypadat takto:
S = ((a 1 + a 2 ) / 2) * √ {v 1 2 - [(a 1 - a 2 ) 2 + v 1 2 - v 2 2 ) / (2 * ] 2 }.
Způsoby výpočtu plochy lichoběžníkového lichoběžníku
První se týká skutečnosti, že do něj může být vložen kruh. A znát její poloměr (je označen písmenem r), stejně jako úhel v základně - γ, můžete použít následující vzorec:
S = (4 * r 2 ) / sin γ.
Druhý obecný vzorec, který je založen na znalostech všech stran této postavy, bude výrazně zjednodušen díky tomu, že strany mají stejný význam:
S = ((a 1 + a 2 ) / 2) * √ {ve 2 - [(a 1 - a 2 ) 2 / (2 * (a 1 - a 2 )) 2 .
Metody výpočtu plochy pravoúhlého lichoběžníku
Je zřejmé, že některý z uvedených pro libovolný tvar udělá. Někdy je však užitečné vědět o jednom prvku takového lichoběžníku. Spočívá ve skutečnosti, že rozdíl čtverců délky diagonálů se rovná rozdílu složenému ze čtverců základen.
Často jsou zapomenuty vzorce pro lichoběžník, zatímco výrazy pro oblasti obdélníku a trojúhelníku jsou zapamatovány. Potom můžete použít jednoduchou cestu. Rozdělte lichoběžník na dva tvary, pokud jsou pravoúhlé nebo tři. Jeden přesně bude obdélník a druhý nebo dva zbývající trojúhelníky. Po výpočtu oblastí těchto čísel je bude přidávat pouze.
To je docela jednoduchý způsob jak najít náměstí trapeze.
Co když jsou známy souřadnice vrcholů lichoběžníku?
V tomto případě budete muset použít výraz, který vám umožní určit vzdálenost mezi body. Může být použit třikrát: aby se učil jak základy, tak jedna výška. A pak použijte první vzorec, který je popsán o něco výše.
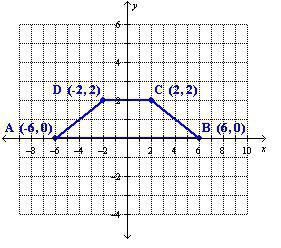
Pro ilustraci této metody můžete uvést příklad. Vzhledem k vrcholům se souřadnicemi A (5; 7); B (8; 7); C (10; 1); D (1; 1). Potřebujete vědět oblast obrázku.
Než najdete oblast lichoběžníku, musíte vypočítat délku základny podle souřadnic. Budete potřebovat následující vzorec:
délka segmentu = √ {(rozdíl prvních souřadnic bodů) 2 + (rozdíl druhých souřadnic bodů) 2 }.
Horní základna je označena AB, což znamená, že její délka bude rovna √ {(8-5) 2 + (7-7) 2 } = √9 = 3. Dolní hodnota bude SD = √ {(10-1) 2 + ) 2 } = √81 = 9.
Nyní musíte udržet výšku od horní části k základně. Nechť je začátek v bodě A. Konec segmentu bude na spodní základně v bodě se souřadnicemi (5; 1), ať to bude bod N. Délka segmentu AN bude rovna √ {(5-5) 2 + (7-1) 2 } = √36 = 6.
Zbývá pouze nahradit výsledné hodnoty do vzorce lichoběžníkového pole:
S = ((3 + 9) / 2) * 6 = 36.
Problém je vyřešen bez jednotek, protože měřítko souřadnicové mřížky není zadáno. Může to být buď milimetr nebo metr.
Příklady úkolů
Č. 1. Podmínka. Známý úhel mezi úhlopříčkami libovolného lichoběžníku je rovný 30 stupňům. Menší úhlopříčka je 3 dm a druhá 2x větší. Je třeba vypočítat plochu lichoběžníku.
Rozhodnutí. Nejprve musíte znát délku druhé diagonály, protože bez toho nemůžete odpověď počítat. Vypočítejte, že je to snadné, 3 * 2 = 6 (dm).
Nyní musíte použít odpovídající vzorec pro oblast:
S = ((3 * 6) / 2) * sin 30 ° = 18/2 * ½ = 4,5 (dm 2 ). Problém byl vyřešen.
Odpověď: plocha lichoběžníku je 4,5 dm 2 .
Č. 2. Podmínka. V lichoběžníku AVSD jsou základny segmenty AD a BC. Bod E je středem strany SD. Od něj je kolmá na přímku AB, konce tohoto segmentu je označen písmenem N. Je známo, že délky AB a EH jsou 5 a 4 cm. Je nutné vypočítat plochu lichoběžníku.
Rozhodnutí. Nejprve musíte vytvořit kresbu. Vzhledem k tomu, že hodnota kolmice je menší než strana, ke které je vedena, lichoběžník bude mírně prodloužen směrem nahoru. EN bude uvnitř obrázku.
Chcete-li jasně vidět průběh úkolu, budete muset provést další konstrukci. Namísto toho nakreslete přímku, která bude rovnoběžná se stranou AB. Průsečíky tohoto řádku s AD - P as pokračováním ozbrojených sil - X. Výsledná hodnota je rovnoběžník. Navíc je jeho plocha rovna požadované oblasti. To je způsobeno skutečností, že trojúhelníky, které se ukázaly jako dodatečné konstrukce, jsou stejné. To vyplývá z rovnosti boku a dvou rohů sousedících s ním, jednoho - svislého, druhého - ležícího křížem.
Plochu paralelogramu naleznete podle vzorce, které obsahuje produkt boku a výšku, která na něj klesla
Takže plocha lichoběžníku je 5 x 4 = 20 cm2.
Odpověď: S = 20 cm 2 .
Č. 3. Podmínka. Prvky lichoběžníkového lichoběžníku mají následující významy: spodní základna je 14 cm, horní část je 4 cm a ostrý úhel je 45 °. Je třeba vypočítat jeho plochu.
Rozhodnutí. Nechte menší základnu označit jako BC. Nadmořská výška z bodu B se nazývá HV. Protože úhel je 45 °, trojúhelník ABH bude obdélníkový a rovnoramenný. AN = BH. Navíc je NA velmi snadné najít. To se rovná polovině základního rozdílu. To je (14 - 4) / 2 = 10/2 = 5 (cm).
Důvody jsou známy, výška je počítána. Můžete použít první vzorec, který byl považován za libovolný lichoběžník.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (cm2).
Odpověď: Požadovaná plocha je 45 cm 2 .
№ 4. Podmínka. K dispozici je libovolný lichoběžníkový AVSD. Na svých stranách jsou odebírány body O a E, takže OE je rovnoběžná se základnou archy. Plocha lichoběžníkového AOED je pětkrát větší než plocha CFE. Vypočte hodnotu OE, pokud jsou známé délky základny.
Rozhodnutí. Bude nutné vybírat dvě paralelní přímky AB: první bod C, jeho průnikem s OE je bod T; druhá až E a průsečíkem AD bude M.
Nechte neznámou OE = x. Výška menšího lichoběžníku CFE je n 1 ;
Vzhledem k tomu, že oblasti těchto dvou lichoběžníků jsou spojeny jako 1 až 5, můžeme napsat následující rovnost:
(x + a 2 ) * n 1 = 1/5 (x + a 1 ) * n 2
nebo
n 1 / n 2 = (x + a 1 ) / (5 (x + a 2 )).
Výšky a strany trojúhelníků jsou úměrné konstrukci. Proto můžeme napsat další rovnost:
n 1 / n 2 = (x - a 2 ) / (a 1 - x).
V posledních dvou položkách na levé straně jsou stejné hodnoty, takže můžete napsat, že (x + a 1 ) / (5 (x + a 2 )) se rovná (x - a 2 ) / (a 1 - x).
To vyžaduje řadu transformací. Nejprve se násobte křížem. Zobrazí se konzoly, které označují rozdíl v polích. Po uplatnění tohoto vzorce získáte krátkou rovnici.
Je třeba otevřít závorky a přesunout všechny výrazy z neznámé "x" na levé straně a poté extrahovat druhá odmocnina.
Odpověď : x = √ {(a 1 2 + 5 a 2 2 ) / 6}.