Binomální distribuce: definice, vzorec, příklady

Teorie pravděpodobnosti je neviditelně přítomna v našich životech. Nevěnujeme tomu, ale každá událost v našem životě má jistou pravděpodobnost. Vzhledem k velkému počtu scénářů je pro nás nezbytné určit nejpravděpodobnější a nejpravděpodobnější z nich. Nejvýhodnější je grafická analýza těchto pravděpodobnostních dat. Distribuce nám může pomoci. Binomial - jeden z nejjednodušších a nejpřesnějších.

Než se obrátíme přímo na matematiku a teorii pravděpodobnosti, pojďme se zabývat tím, kdo nejprve přišel s tímto druhem distribuce a jaká je historie vývoje matematického aparátu pro tento koncept.

Dějiny

Pojetí pravděpodobnosti je známo od starověku. Starověcí matematici však nepřikládali velkou důležitost a byli schopni položit jen základy teorie, která se později stala teorií pravděpodobnosti. Vytvořili některé kombinatorické metody, které značně pomohly těm, kteří později vytvořili a rozvinuli samotnou teorii.

Ve druhé polovině sedmnáctého století začalo vytváření základních pojmů a metod teorie pravděpodobnosti. Byly zavedeny definice náhodných proměnných, metody výpočtu pravděpodobnosti jednoduchých a některých složitých nezávislých a závislých událostí. Takový zájem o náhodné proměnné a pravděpodobnosti diktoval hazard: každý chtěl vědět, jaké jsou jeho šance na výhru hry.

Dalším krokem bylo použití metod v teorii pravděpodobnosti matematická analýza. Vynikající matematici, jako jsou Laplace, Gauss, Poisson a Bernoulli, se tento úkol ujali. Vyvinuli tuto oblast matematiky na novou úroveň. Právě James Bernoulli objevil binomický distribuční zákon. Mimochodem, jak se dozvíme později, bylo na základě tohoto objevu provedeno několik dalších, které umožnily vytvořit zákon o normální distribuci a mnoho dalších.

Nyní, než začneme popisovat rozdělení binomického čísla, trochu osvěžíme pojmy teorie pravděpodobnosti, pravděpodobně již zapomenuté ze školy.

Základy teorie pravděpodobnosti

Uvažujeme o takových systémech, v jejichž důsledku jsou možné pouze dva výsledky: "úspěch" a "neúspěch". Toto je snadné pochopit s příkladem: hodíme minci a odhadujeme, že ocasy budou vypadat. Pravděpodobnost každé z možných událostí (úchyty vypadají - "úspěch", orel vypadne - "ne úspěch") je 50 procent s dokonalým vyrovnáním mince a nepřítomnost dalších faktorů, které mohou ovlivnit experiment.

Byla to nejjednodušší událost. Existují však také složité systémy, ve kterých jsou prováděny postupné akce a pravděpodobnosti výsledků těchto akcí se budou lišit. Zvažte například takový systém: v krabici, jejíž obsah nevidíme, jsou šest zcela shodných koulí, tři páry modré, červené a bílé. Musíme dostat několik náhodných míčů. Tím, že nejprve vytáhneme jednu z bílých koulí, budeme občas snižovat pravděpodobnost, že další bude mít také bílou kouli. K tomu dochází, protože počet objektů v systému se mění.

V další části se podíváme na složitější matematické pojmy, které nás vedou k tomu, co znamenají slova "normální distribuce", "binomická distribuce" a podobně.

Prvky matematické statistiky

Ve statistice, která je jednou z oblastí uplatnění teorie pravděpodobnosti, existuje mnoho příkladů, kdy data pro analýzu nejsou výslovně uvedena. To znamená, že není číselné, ale ve formě rozdělení podle označení, například podle pohlaví. Za účelem použití matematického přístroje k takovýmto údajům a vyvození jakýchkoli závěrů z dosažených výsledků je nutné převést původní údaje do číselného formátu. Pro dosažení tohoto cíle je pozitivním výsledkem přiřazena hodnota 1 a záporná hodnota je přiřazena hodnotě 0. Získáme tak statistické údaje, které lze analyzovat pomocí matematických metod.

Dalším krokem v pochopení toho, co je binomické rozdělení náhodné proměnné, je určit odchylku náhodné proměnné a matematické očekávání. To je popsáno v další části.

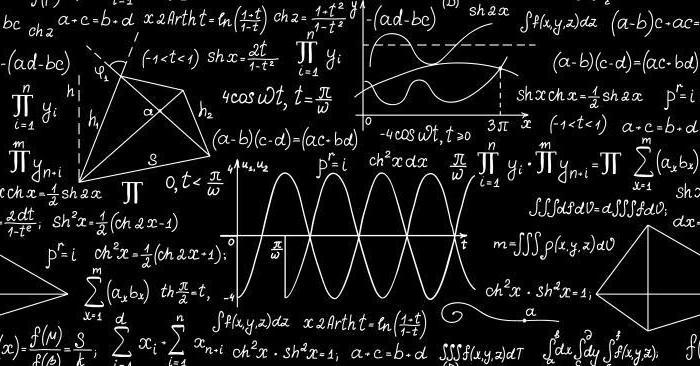
Matematické očekávání

Ve skutečnosti je snadné pochopit, co je očekávání. Zvažte systém, ve kterém existuje mnoho různých událostí s různými pravděpodobnostmi. Matematická očekávání se nazývá hodnota shodná s součtem produktů hodnot těchto událostí (a matematické formy, o které jsme se diskutovali v poslední části) o pravděpodobnosti jejich realizace.

Matematické očekávání binomického rozdělení se vypočítá podle stejného schématu: vezmeme hodnotu náhodné proměnné, vynásobíme ji pravděpodobností pozitivního výsledku a shrneme data získaná pro všechna množství. Je velmi výhodné prezentovat tyto údaje graficky - tím je lepší vnímat rozdíl mezi matematickými očekáváními různých veličin.

V další části vám něco řekneme o dalším konceptu - rozptylu náhodné proměnné. Je také úzce spjata s takovou koncepcí jako binomické rozdělení pravděpodobnosti a je její charakteristickou charakteristikou.

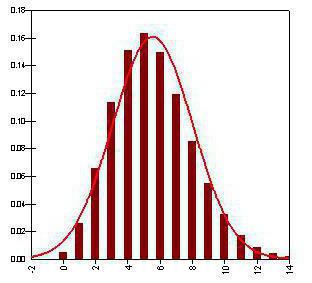
Rozpor binomického rozdělení

Tato hodnota úzce souvisí s předchozím a také charakterizuje distribuci statistických dat. Představuje průměrný čtverec odchylek hodnot od jejich očekávání. To znamená, že rozptyl náhodné proměnné je součet čtverců rozdílů mezi hodnotou náhodných proměnných a jejich očekáváním vynásobený pravděpodobností této události.

Obecně platí, že toto je vše, co potřebujeme vědět o rozptylu, abychom pochopili, co je binomální distribuce pravděpodobnosti. Nyní se obracíme přímo k našemu hlavnímu tématu. Namísto toho, co spočívá za takovou zdánlivě poměrně složitou větou "zákon o binomické distribuci".

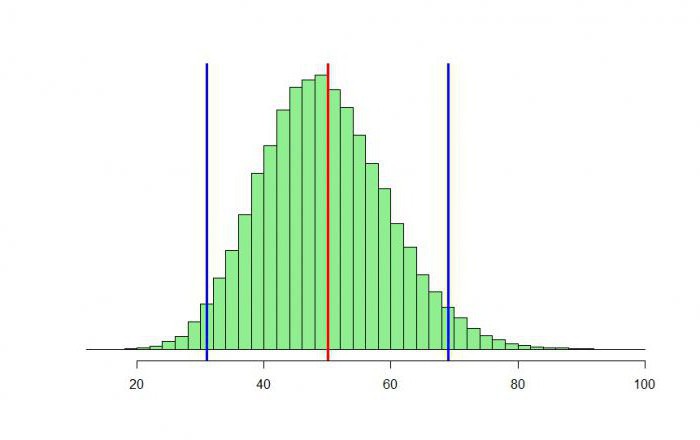
Binomální distribuce

Nejprve pochopíme, proč je toto rozdělení binomické. Pochází ze slova "bin". Možná jste slyšeli o binomii Newtonu - vzorec, s nímž můžete rozložit součet dvou libovolných čísel a a b do libovolného negativního stupně n.

Jak jste pravděpodobně již uhádli, binomický vzorec Newtonu a binomický distribuční vzorec jsou téměř identické vzorce. Pouze s výjimkou, že druhá má aplikovanou hodnotu pro specifická množství, a první je pouze obecný matematický nástroj, jehož aplikace mohou být v praxi odlišné.

Distribuční vzorce

Funkci binomické distribuce lze zapsat jako součet následujících členů:

(n! / (nk)! k!) * p ^k * q ^nk

Zde n je počet nezávislých náhodných experimentů, p je počet úspěšných výsledků, q je počet neúspěšných výsledků, k je číslo experimentu (může mít hodnoty od 0 do n),! - označení faktoriální funkce, funkce čísla, jejíž hodnota se rovná součinu všech čísel, které dosáhly (např. pro číslo 4: 4! = 1 * 2 * 3 * 4 = 24).

Navíc funkce binomické distribuce může být zapsána jako neúplná beta funkce. Jedná se však o složitější definici, která se používá pouze při řešení složitých statistických problémů.

Binomické rozložení, které jsme uvažovali výše, je jedním z nejjednodušších druhů rozdělení v teorii pravděpodobnosti. Existuje také normální rozdělení, což je typ binomického typu. Používá se nejčastěji a nejjednodušší ve výpočtech. Existuje také distribuce Bernoulli, distribuce Poisson, podmíněné rozdělení. Všechny z nich graficky charakterizují pravděpodobnosti procesu za různých podmínek.

V další části se podíváme na aspekty týkající se používání tohoto matematického přístroje v reálném životě. Na první pohled se samozřejmě zdá, že se jedná o další matematickou věc, která jako obvykle nenachází žádnou aplikaci v reálném životě a nikdo jiný kromě samotných matematiků vůbec nepotřebuje. To je však daleko od případu. Koneckonců, všechny typy distribucí a jejich grafické znázornění byly vytvořeny výlučně pro praktické účely a ne jako rozmar vědců.

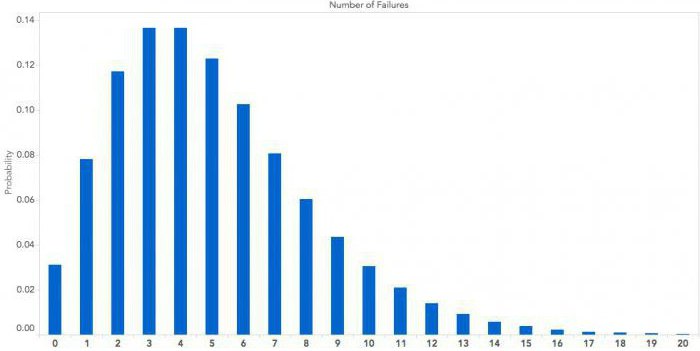
Aplikace

Samozřejmě, nejdůležitější použití distribuce nalezené ve statistice, protože potřebují komplexní analýzu souboru dat. Jak ukazuje praxe, mnoho datových polí má přibližně stejnou distribuci hodnot: kritické oblasti s velmi nízkými a velmi vysokými hodnotami zpravidla obsahují méně elementů než průměrné hodnoty.

Analýza velkého množství údajů je nutná nejen ve statistikách. Je nepostradatelná například ve fyzikální chemii. V této vědě se používá k určení množství veličin, které jsou spojeny s náhodnými kmity a pohyby atomů a molekul.

V další části si ukážeme, jak důležité je použití takových statistických pojmů jako binomické distribuce náhodných proměnných v každodenním životě pro vás i pro mě.

Proč to potřebuji?

Mnoho lidí si tuto otázku položí, pokud jde o matematiku. A mimochodem, matematika není pro nic nazývána královnou vědy. Je základem fyziky, chemie, biologie, ekonomie a v každé z těchto věd se uplatňuje také určité rozložení: zda toto diskrétní binomické rozdělení, nebo normální, není důležité. A když se blíže podíváme na svět kolem nás, uvidíme, že matematika je používána všude: v každodenním životě, v práci a dokonce i v lidských vztazích lze reprezentovat jako statistické údaje a analyzovat (mimochodem, ti, kteří pracují v zvláštní organizace, které shromažďují informace).

Nyní mluvte trochu o tom, co dělat, pokud potřebujete vědět o tomto tématu mnohem víc než to, co jsme v tomto článku naznačili.

Co jiného můžete číst?

Informace, které jsme uvedli v tomto článku, nejsou zdaleka úplné. Existuje mnoho nuancí ohledně toho, jaká forma distribuce může trvat. Binomální distribuce, jak jsme již zjistili, je jedním z hlavních typů, na kterých jsou založeny všechny matematické statistiky a teorie pravděpodobnosti.

Pokud se vám to zajímalo nebo v souvislosti s vaší prací potřebujete vědět mnohem víc o tomto tématu, budete muset studovat odbornou literaturu. Měli bychom začít matematickou analýzou univerzity a dostat se do teorie pravděpodobnosti. Bude to také užitečné znalosti v oblasti sérií, protože binomické rozdělení pravděpodobnosti není nic jiného než řada po sobě jdoucích členů.

Závěr

Před dokončením článku bychom chtěli ještě jednu zajímavou věc vyprávět. Týká se přímo tématu našeho článku a celé matematiky obecně.

Mnoho lidí říká, že matematika je zbytečná věda a nic, co prošly ve škole, se jim hodilo. Znalost však není nikdy nadbytečná a pokud vám něco v životě není prospěšné, znamená to, že si to prostě nepamatuješ. Pokud máte znalosti, mohou vám pomoci, ale pokud tam nejsou, není třeba čekat na pomoc od nich.

Takže jsme se podívali na koncept binomického rozdělení a všech souvisejících definic a mluvili o tom, jak to platí pro náš život.