Rovnovážný stav páky. Pravidlo okamžiků. Jednoduché mechanismy. Úkoly a řešení
Od nepaměti lidstvo používá různé mechanismy, které jsou určeny k usnadnění fyzické práce. Jedním z nich je páka. Co je to, co je myšlenka jeho použití a jaká je podmínka rovnováhy páky, tento článek je věnován úvahám o všech těchto otázkách.
Kdy lidstvo začalo uplatňovat princip pákového efektu?

Je obtížné odpovědět na tuto otázku přesně, protože již staré Egypťany a obyvatelé Mezopotámie již známi jednoduché mechanismy již tři tisíce let před naším letopočtem.
Jedním z těchto mechanismů je tzv. Pákový jeřáb. Představoval dlouhý pól, který byl umístěn na podpěře. Ten byl instalován blíž k jednomu konci tyče. Ke konci, který byl dále od referenčního bodu, svázali loď, na druhé straně položili nějakou protiváhu, například kámen. Systém byl nastaven tak, aby nádoba naplněná polovinou vedla k horizontální poloze tyče.
Ad
Pákový jeřáb sloužil ke zvednutí vody ze studny, řeky nebo jiné deprese na úroveň, kde byla osoba. Aplikuje na plavidlo malou sílu osoba, která ji splachovala k vodnímu zdroji, nádoba byla naplněna kapalinou a pak se na druhém konci stožáru natlačila malá síla s protizávažím, bylo možné zvednout indikovanou nádobu.
Legenda Archimedes a Loď
Každý zná starověký řecký filozof z města Syracuse, Archimedes, který ve svých spisech nejen popsal princip fungování jednoduchých mechanismů (páka, nakloněná deska), ale také vyústil v odpovídající matematické vzorce. Až dodnes je jeho fráze slavná:
Dejte mi oporu a já tento svět přemístím!

Jak víte, nikdo mu nedal takovou podporu a Země zůstala na svém místě. Nic, co se Archimedes skutečně dokázal pohybovat, byla loď. Jedna z legend o Plutarchovi (dílo "Paralelní životy") říká následující: Archimedes v dopise svému příteli, králi Hieronovi ze Syrakusy, řekl, že za určitých podmínek může sám volit libovolně velkou váhu. Hieron byl překvapen takovým prohlášením filozofa a požádal jej, aby ukázal, o čem mluví. Archimedes souhlasil. Jeden z dnů, loď Hieron, v doku, byla naložena lidmi a barely naplněnými vodou. Filozof, který seděl v dálce od lodi, dokázal ho zvednout nad vodu, vytáhnout lana a přitom se snažit trochu.
Součásti páky
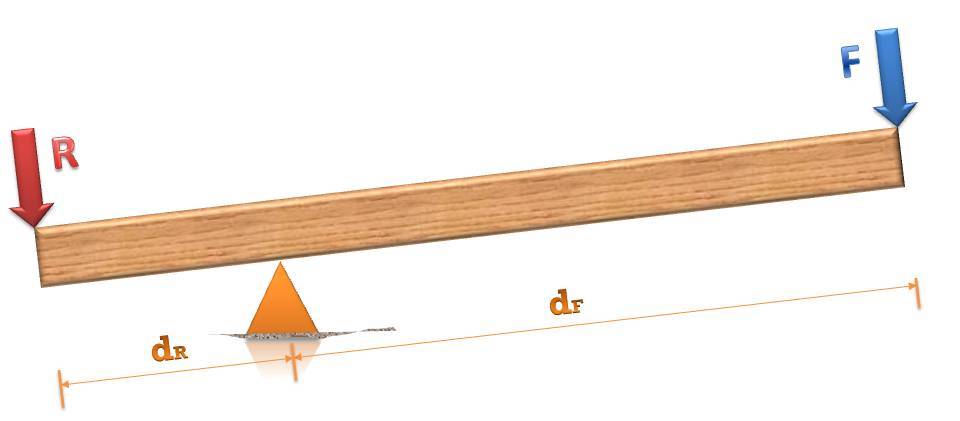
Navzdory skutečnosti, že mluvíme o poměrně jednoduchém mechanismu, stále má určité zařízení. Fyzicky se skládá ze dvou hlavních částí: tyče nebo nosníku a podpěry. Při zvažování stejných úkolů se pól považuje za objekt sestávající ze dvou (nebo jedné) ramen. Rameno je součástí stožáru, který je vzhledem k podpěře na jedné straně. Velkou roli v principu fungování sledovaného mechanismu je přesně délka ramene.
Při zvažování páky v práci existují dva další prvky: přiložená síla a síla proti ní. První se snaží dát do pohybu objekt, který vytváří sílu opozice.
Ad
Rovnovážný stav pákového efektu ve fyzice
Seznámení se zařízením tohoto mechanismu předkládáme matematický vzorec, pomocí něhož můžeme říci, kterou rameno páky se bude pohybovat v jakém směru nebo naopak celé zařízení bude v klidu. Vzorec má podobu:
F 1 * 1 1 = F 2 * 1 2 ,
kde F 1 a F 2 jsou síly působení a reakce, respektive, l 1 a l 2 jsou délky ramen, kterým jsou tyto síly aplikovány.
Tento výraz umožňuje prozkoumat podmínky rovnováhy páky s osou rotace. Pokud je tedy rameno l 1 větší než l 2 , pak k vyvážení síly F 2 potřebujete menší hodnotu F 1 . Naopak, pokud l 2 > l 1 , pak k potlačení síly F 2 budete muset připojit velký F 1 . Tyto závěry lze získat přepsáním výše uvedeného výrazu v následující podobě:
Ad
F 1 / F 2 = l 2 / l 1 .
Jak je vidět, síly podílející se na procesu vytváření rovnováhy jsou nepřímo spojené s délkou ramen páky.
Jaký je zisk a ztráta při použití páky?
Důležitý závěr vyplývá z výše uvedených vzorců: pomocí dlouhé paže a malého úsilí lze objekty s obrovskou hmotností pohybovat. To je pravda a mnozí si mohou myslet, že použití páky vede k nárůstu práce. Ale není. Práce je množství energie, které nelze z ničeho vytvořit.
Podívejme se na práci jednoduché páky mající dvě vytvrzování l 1 a l 2 . Předpokládejme, že na konci ramene l 2 je hmotnost P (F 2 = P). Na konci druhého ramena použije osoba sílu F 1 a zvedne toto zatížení do výšky h. Nyní vypočteme práci každé síly a porovnáme získané výsledky. Máme:
Ad
F 1 * x = F 2 * h.
Síla F 2 působila podél svislé trajektorie délky h, zase F 1 působila také podél svislice, ale byla již připojena k druhému rameni, jehož konec se pohyboval neznámým množstvím x. Abychom to našli, je nutné v posledním výrazu nahradit vzorec spojení mezi silami a rameny páky. Vyjadřujeme x, máme:
x = F 2 * h / F 1 = l 1 * h / l 2 .
Tato rovnost ukazuje, že pokud l 1 > 2 , pak F 2 > F 1 a x> h, tj. Pomocí malé síly, můžete zvednout zatížení s velkou hmotností, ale musíte přemístit příslušné pákové rameno (l 1 ) na větší. vzdálenosti. Naopak pokud l 1 < 2 2 , pak F 2 <F 1 a x <h, tj. Váha určité hmotnosti může být zvýšena na větší výšku h pohybem ramene l 1 na menší amplitudu, ale musíte aplikovat dostatečně velkou sílu F 1 . V prvním případě je dosaženo zisku v síti, v druhém způsobu nebo rychlosti.
Páka tedy v práci nemá prospěch, ale umožňuje pouze její redistribuci buď ve prospěch menší aplikované síly, nebo ve prospěch větší amplitudy pohybu objektu. Obecný filozofický princip pracuje v předmětu fyziky v diskusi: každý zisk je kompenzován určitou ztrátou.
Typy páček
V závislosti na bodech působení síly a na poloze podpěry se rozlišují tyto typy mechanismu:
- Prvním druhem: otazník je mezi dvěma silami F 1 a F 2 , proto délka ramen určuje, co dává takovou výhodu. Příkladem jsou obyčejné nůžky.
- Druhý druh. Zde působí síla, proti které se pracuje, mezi nosnou a působící silou. Tento typ konstrukce znamená, že vždy přinese sílu a ztrátu jízdy a rychlosti. Jeho příkladem je zahradní auto.
- Třetí druh. Poslední možností, kterou je třeba dosáhnout v tomto jednoduchém provedení, je poloha aplikované síly mezi nosnou a odporovou silou. V tomto případě zisk v cestě, ale ztráta je v platnosti. Příkladem by bylo pinzeta.

Koncept momentu síly
Zvažování jakýchkoli problémů v mechaniky, které zahrnují koncepce osy nebo bodu otáčení, se provádí pomocí pravidla momentu síly. Vzhledem k tomu, že opěra páky je také osou (bodem), kolem níž se systém otáčí, moment momentu se rovněž používá k odhadu rovnováhy tohoto mechanismu. Tímto se míní množství ve fyzice, které se rovná výsledku ramena a působící síly, to znamená:
M = 1 * F.
Vzhledem k této definici může být stav pákové rovnováhy přepsán následovně:
M 1 = M 2 , kde M 1 = l 1 * F 1 a M 2 = l 2 * F 2 .
Moment M je aditivní, což znamená, že celkový moment síly pro daný systém lze získat obvyklým přidáním všech momentů M i, které na něm působí. Měli bychom však vzít v úvahu jejich znamení (síla, která způsobuje, že se systém otočí proti směru hodinových ručiček, vytvoří pozitivní moment + M a naopak). S tím se říká, že pravidlo momentů pro páku, která je v rovnováze, bude vypadat takto:
Ad
M 1 - M 2 = 0.
Páčka ztratí rovnováhu, když M 1 ≠ M 2 .
Kde se používá princip pákového efektu?
Již jsme uvedli několik příkladů použití tohoto jednoduchého a známého mechanismu z dávných dob. Zde jsou jen některé další příklady:
- Kleště: páčka 1. druhu, která vám umožní vytvořit obrovské úsilí díky malé délce ramen l 2, kde jsou umístěny zuby nástroje.
- Otvíráky víčka plechovky a lahve: jedná se o páku druhého druhu, takže vždy přináší zisk ve snaze.
- Rybářská tyč: páčka třetího druhu, která umožňuje pohyb konce rybářského prutu plovákem, plattem a hákem pro velké amplitudy. Ztráta v tomto případě se projevuje, když rybář obtížně dostává ryby z vody, i když jejich hmotnost nepřesahuje 0,5 kg.

Muž sám se svými klouby, svaly, kosti a šlachy je živým příkladem systému s mnoha různými pákami.
Řešení problémů
Rovnovážný stav páky popsané v článku se používá k vyřešení jednoduchého problému. Je nutné vypočítat přibližnou délku ramene ramena páky, při níž se Arcimedes dokázal zvednout loď, jak to popisuje Plutarch.

K vyřešení uvádíme následující předpoklady: vezmeme v úvahu řecké trirem 90 tun s posunem a předpokládáme, že podpora páky byla 1 metr od středu hmoty. Vzhledem k tomu, že Archimedes podle legendy mohl loď snadno zvednout, předpokládáme, že pro tento účel použil sílu rovnající se polovině jeho hmotnosti, tj. Asi 400 N (pro hmotnost 82 kg). Potom pomocí rovnovážného stavu páky získáme:
F 1 * l 1 = F 2 * l 2 => l 1 = F 2 * l 2 / F 1 = m * g * l 2 / F 1 = 90000 * 9.81 * 1/400 ≈ 2.2 km.
Dokonce i když budeme zvyšovat sílu aplikovanou na hodnotu hmotnosti samotného Archimedes a přinést podporu ještě dvakrát, pak bude délka ramene asi 500 metrů, což je také velká hodnota. S největší pravděpodobností je legenda o Plutarchu přehnaná, aby demonstrovala účinnost páky, a Archimedes ve skutečnosti nezvedl loď nad vodu.