Důkazy a vlastnosti svislých úhlů
Dvě řady, které se v jednom bodě protínají, se nacházejí nejen v matematice, ale i v každodenním životě. Můžeme je pozorovat, když se podíváme na nůžky, na dvou zkřížených rovných větvích stromů. Pravidelně se s nimi setkáváme v architektonických objektech, strojírenství, v různých mechanismech a dalších objektech. Příklady mohou být hromadné. Tvarované rohy na křižovatce tvoří základ geometrie a jsou studovány dětmi ve středních třídách.

Určení vertikálních úhlů v matematice
Vertikální úhly jsou dva úhly tvořené průsečíkem dvou přímek v jednom bodě. Strany jednoho rohu jsou v tomto případě vždy pokračováním druhého. Takže svislé úhly jsou navzájem protilehlé v protínajících se přímkách se společným průsečíkem.
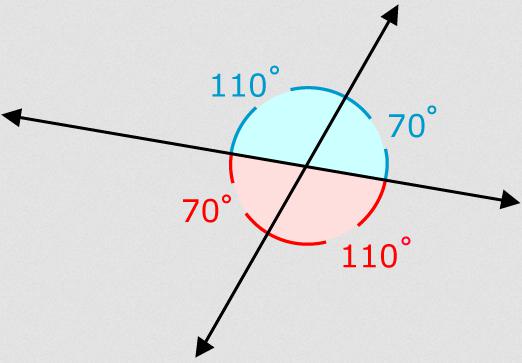
Vlastnosti vertikálního úhlu
Řešením různých problémů v geometrii musí dítě nejprve určit, s čím se zabývá. To je, především, studuje tvar postavy, s níž začíná pracovat. Za to se spoléhá na vlastnosti všech svých slavných osobností. Vlastnosti svislých úhlů pomáhají snadno vytvořit v hlavě algoritmus pro řešení problému:
- Dvě přímé linie, které se v jednom bodě protínají, tvoří dva páry úhlů.
- Vertikální úhly vytvořené proti sobě jsou stejné.
- Součet všech úhlů v průsečíku dvou přímek v jednom bodě je 360 °.
- Sousední úhly tvoří polovinu svislých úhlů.
Při vytváření přímky s jedním průsečíkem jsou vytvořeny dva svislé úhly a čtyři sousední. Jedním z důkazů rovnosti svislých úhlů je rovnost součtu úhlů stupňů 1 + 2 a 3 + 4. V obou sousedních a svislých úhlech, je-li znám jeden z úhlů, druhá může být vypočtena jednoduchým způsobem. Zjistíte-li, jaké vlastnosti mají svislé úhly, můžete rychle určit druhý úhel. Pokud odečteme známý úhel od 180 °, pak známe velikost druhého.