Jak najít sinus úhlu

Sine je jedna ze základních trigonometrických funkcí, jejichž použití není omezeno pouze na geometrii. Tabulky pro výpočet trigonometrických funkcí, stejně jako inženýrské kalkulačky, nejsou vždy po ruce a někdy výpočet sinusu je potřebný pro řešení různých problémů. Obecně platí, že výpočet sinusu přispěje ke konsolidaci návrhových dovedností a znalostí o trigonometrické identitě.

Hry s pravítkem a tužkou

Jednoduchý úkol: jak najít sine úhlu natočeného na papíře? Budete potřebovat standardní pravítko, trojúhelník (nebo kompas) a tužku. Nejjednodušší způsob, jak vypočítat sinus úhlu, může být dělení vzdálené nohy trojúhelníku pravým úhlem na dlouhé straně - hypotenzu. Proto musíte nejdříve přidat obrázek k ostrému úhlu. pravý trojúhelník vykreslování čáry kolmé k jednomu z paprsků v libovolné vzdálenosti od horní části rohu. Bude nutné udržovat úhel přesně o 90 °, pro který budeme potřebovat papírový trojúhelník.

Použití kompasu je trochu přesnější, ale trvá déle. Na jednom z paprsků je třeba určitou vzdálenost označit dvěma body, nastavit poloměr přibližně rovnající se vzdálenosti mezi body na kompasu a nakreslit polokruhy se středy v těchto bodech, dokud se nedosáhnou průsečíky těchto linií. Spojením křižovatek našich kruhů k sobě máme přísnou kolmici na paprsek našeho úhlu, zůstává pouze rozšířit linku na křižovatku s jiným paprskem.

Ve výsledném trojúhelníku musíte měřit s pravítkem protilehlou stranou úhlu a dlouhou stranou na jednom z paprsků. Poměr prvního měření k druhému a bude požadovanou hodnotou sinusu ostrého úhlu.

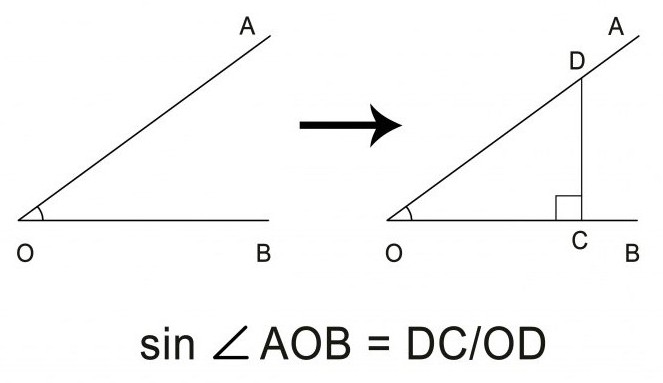
Najít sinus pro úhel větší než 90 °

Pro nudný úhel není úkol mnohem obtížnější. Je nutné nakreslit paprsek z vrcholu v opačném směru pomocí pravítka, aby vytvořila přímku s jedním z paprsků úhlu zájmu. Výsledný ostrý úhel by měl být proveden tak, jak je popsáno výše, siny sousedních úhlů, tvořící společně rozložený úhel 180 °, jsou stejné.

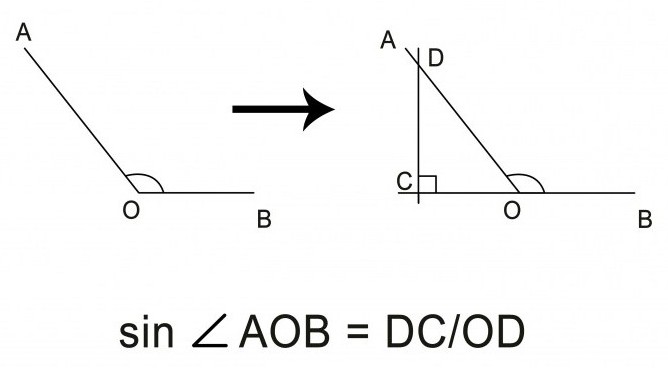
Výpočet sinusu pro jiné trigonometrické funkce

Výpočet sinusů je také možný, pokud jsou známy hodnoty jiných trigonometrických funkcí úhlu nebo alespoň délky stran trojúhelníku. To nám pomůže s trigonometrickou identitou. Podívejme se na běžné příklady.

Jak najít sinus u známého kosinus úhlu? První trigonometrická identita, odvozená z Pythagorovy věty, uvádí, že součet čtverců sinus a kosinus se stejným úhlem se rovná jednomu.

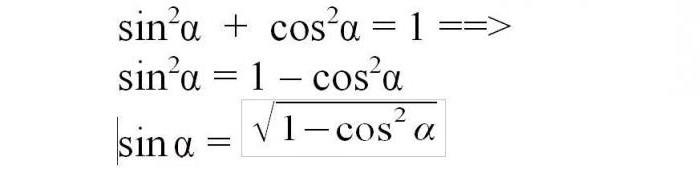
Jak zjistit sinus u známé tečny úhlu? Tangent je získán dělením vzdálené nohy uprostřed nebo dělením sinusu kosinusem. Takže sinus je součinem kosinusu a tečny a čtverce sinusu je čtvercem tohoto produktu. Nahraďte kosinus na čtverec rozdílem mezi jednotkou a čtvercovým sinusem podle první trigonometrické identity a jednoduchými manipulacemi dáváme rovnici pro výpočet čtvercového sinusu tangensem, aby vypočítala, že sinus bude muset extrahovat kořen výsledku.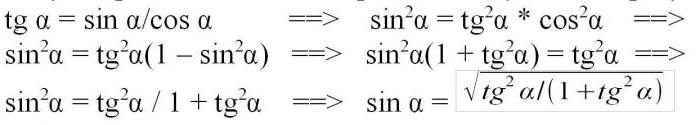

Jak najít sinus v známém úhlu kotangent? Hodnota kotangentu může být vypočtena dělením délky blízké nohy z úhlu nohy dlouhou vzdáleností a dělením kosinusu sinusem, to znamená, že kotangent je funkce inverzní k tangentu čísla 1. Pro výpočet sinusu můžete vypočítat tangens vzorce tg α = 1 / ctg α a použijte vzorec ve druhé verzi. Můžete také odvodit přímý vzorec analogicky s tečkou, která bude vypadat takto.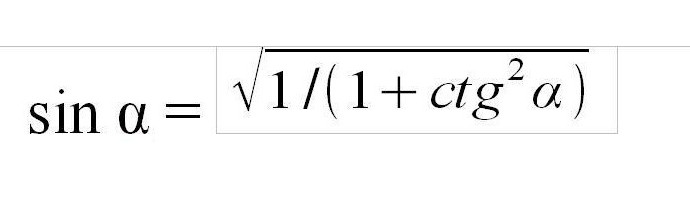

Jak najít sinus na třech stranách trojúhelníku

Existuje vzorec pro nalezení délky neznámé strany jakéhokoli trojúhelníku, a to nejen pravoúhlého, na dvou známých stranách s použitím funkce trigonometrického kosinu protilehlého úhlu. Vypadá to takhle.

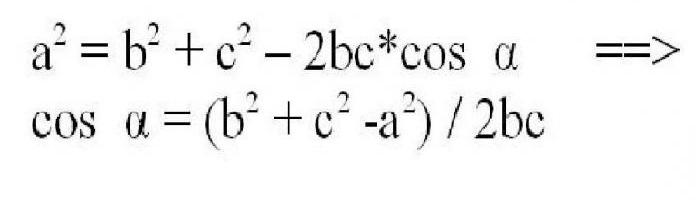Sine může být dále vypočítána kosinem podle výše uvedených vzorců.