Jak správně snížit zlomky?

Frakce a jejich redukce - další téma, které začíná v 5. třídě. Zde se vytváří základ této akce a pak jsou tyto dovednosti přitahovány nití k vyšší matematice. Pokud se student nenaučil, jak snížit zlomky pak může mít problémy s algebry. Proto je lepší pochopit několik pravidel jednou provždy. A pamatujte si jeden zákaz a nikdy jej neporušujte.

Frakce a její snížení

Co to je, každý student to ví. Jakékoli dvě číslice mezi vodorovnou čárou jsou okamžitě vnímány jako zlomky. Nicméně, ne každý pochopí, že to může být libovolné číslo. Je-li to celé číslo, pak může být vždy děleno jedním, pak dostaneme zlý zlomek. Ale o tom později.

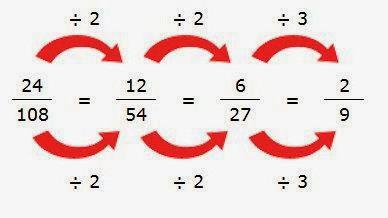
Začátek je vždy jednoduchý. Nejprve musíte zjistit, jak snížit správnou frakci. To je ten, jehož čitatel je menší než jmenovatel. K tomu musíte pamatovat hlavní vlastnost zlomku. Tvrdí, že vynásobením (stejně jako rozdělením) jeho čitatele a jmenovatele stejným číslem současně je ekvivalentní původní části.

Rozdělit akce, které jsou prováděny v této vlastnosti a vedou ke snížení. To znamená jeho maximální zjednodušení. Frakci lze snížit, pokud existují společné faktory nad a pod čárou. Když jsou pryč, snížení je nemožné. A říkají, že tento zlomek je neredukovatelný.

Dva způsoby

1. Snižte krok za krokem. Používá metodu odhadu, když obě čísla jsou dělena minimálním společným faktorem, který si student všiml. Pokud po první kontrakci vidíme, že to není konec, rozdělení pokračuje. Dokud se zlomek nezmění.

2. Hledání největšího společného dělitele čitatele a jmenovatele. To je nejvíce racionální způsob, jak snížit zlomky. Zahrnuje rozklad čitatele a jmenovatele na primární faktory. Mezi nimi pak musíte zvolit totéž. Jejich výrobek dá největší společný faktor, což je snížená frakce.

Obě tyto metody jsou ekvivalentní. Student je vyzván, aby je zvládl a používal ten, který se mu nejvíce líbil.

Co když jsou písmena a akce sčítání a odečítání?

První část otázky je více či méně jasná. Písmena mohou být zkrácena jako čísla. Hlavní věc je, že fungují jako multiplikátory. Ale s druhým, mnozí mají problémy.

Je důležité si pamatovat! Můžete omezit pouze čísla, která jsou multiplikátory. Jsou-li to podmínky, je to nemožné.

Abyste pochopili, jak snižovat frakce, které mají podobu algebraického výrazu, musíte se naučit pravidlo. Nejprve představte čitatele a jmenovatele ve formě díla. Pak můžete snížit, pokud existují společné faktory. Pro reprezentaci ve formě násobitelů jsou užitečné následující techniky:

• seskupení;
• uložení držáku;
• použití identit zkráceného násobení.

Navíc tato druhá metoda umožňuje okamžitě získat termíny ve formě násobitelů. Proto musí být vždy použita, pokud je známý vzorek viditelný.

Ale to není strašné, objeví se úkoly se stupněmi a kořeny. Tehdy budete potřebovat odvahu a naučit se pár nových pravidel.

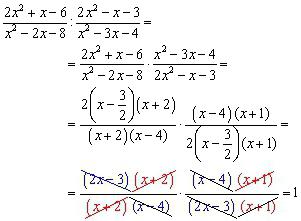
Exprese se stupněm

Frakce V čitatele a jmenovateli. Jsou tu písmena a čísla. A jsou také zvednuty k síle, která také obsahuje termíny nebo faktory. Je tu něco, čeho se bojíte.

Abyste zjistili, jak snižovat zlomky se stupni, musíte se naučit dvě věci:

• pokud je exponent součtem, pak se může rozšířit na faktory, jejichž stupně budou původní;
• pokud je rozdíl dělitelný a dělitelný, první bude mít pokles stupně a druhý bude odpočitatelný.

Po provedení těchto akcí se stanou běžnými faktory viditelnými. V takových příkladech není nutné vypočítat všechny stupně. Stačí jen snížit stupně se stejnými indikátory a základy.

Abyste se nakonec dozvěděli, jak snižovat zlomky se stupni, musíte hodně cvičit. Po několika příkladech stejného typu budou akce prováděny automaticky.

A pokud je výraz kořen?

Může se také snížit. Ale opět, podle pravidel. A všechny ty, které byly popsány výše, jsou pravdivé. Obecně platí, že pokud existuje otázka, jak snížit zlomek s kořeny, musíte je rozdělit.

Iracionální výrazy lze také rozdělit. To znamená, že pokud čitatel a jmenovatel jsou stejné faktory uzavřené pod znamením kořene, pak mohou být bezpečně sníženy. To zjednoduší výraz a provede úkol.

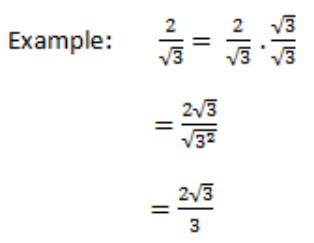
Pokud po redukci pod čárou frakce zůstává iracionalita, pak je nutné ji zbavit. Jinými slovy vynásobte čitateli a jmenovatele. Pokud po této operaci existují společné faktory, je třeba je znovu snížit.

Tady je možná všechno, jak snížit zlomky. Existuje jen málo pravidel, ale jeden zákaz. Nikdy zkrátit podmínky!