Rotující pohyb těla. Zákon rotačního pohybu

Tento článek popisuje důležitou část fyziky - "Kinematika a dynamika rotačního pohybu".

Základní pojmy kinematiky rotačního pohybu

Rotační pohyb materiální bod kolem pevné osy se nazývá takový pohyb, jehož trajektorií je kružnice umístěná v rovině kolmé k ose a její střed leží na ose rotace.

Rotující pohyb pevného těla je pohyb, ve kterém se všechny body těla pohybují podél soustředných kružnic (jejichž středy leží na stejné ose) v souladu s pravidlem rotačního pohybu bodu materiálu.

Nechte libovolné pevné těleso T otáčet kolem osy O, která je kolmá na rovinu obrázku. Na tomto těle zvolte bod M. Během otáčení bude tento bod popisovat kružnici o poloměru r kolem osy O.

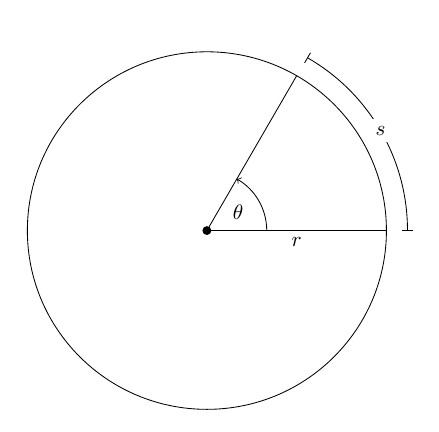
Po určitém čase se poloměr otočí vzhledem k počáteční poloze o úhel Δφ.

Směr pravého šroubu (ve směru hodinových ručiček) je považován za pozitivní směr otáčení. Změna úhlu natočení s časem se nazývá rovnice rotačního pohybu pevné látky:

φ = φ (t).

Je-li φ měřeno v radiánech (1 rad je úhel odpovídající oblouku o délce rovnající se jeho poloměru), pak délka oblouku kružnice ΔS, kterou materiálový bod M projde během času Δt, se rovná:

ΔS = Δφr.

Hlavní prvky kinematiky jednotného rotačního pohybu

Měření pohybu materiálu bodu v krátkém časovém úseku dt je elementární vektor rotace dφ .

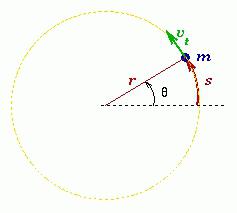
Úhlová rychlost Materiální bod nebo tělo je fyzikální veličina, která je určena poměrem vektoru elementární rotace k době trvání této rotace. Směr vektoru lze určit pravidlem pravého šroubu podél osy O. Ve skalární podobě:

ω = dφ / dt.

Pokud ω = dφ / dt = const, pak se takový pohyb nazývá rovnoměrným rotačním pohybem. Když je úhlová rychlost určena vzorem

ω = φ / t.

Podle předběžného vzorce je rozměr úhlové rychlosti

[ω] = 1 rad / s.

Rovnoměrný rotační pohyb těla může být popsán obdobím rotace. Období rotace T je fyzikální veličina, která určuje dobu trvání těla kolem osy otáčení k provedení jedné úplné otáčky ([T] = 1 s). Pokud ve vzorci pro úhlovou rychlost vzít t = T, φ = 2 π (plná poloměr otáčení r), pak

ω = 2π / T,

Proto je období rotace definováno takto:

T = 2π / ω.

Počet otáček, které těleso dělá za jednotku času, se nazývá frekvence rotace ν, která se rovná:

ν = 1 / T.

Frekvenční jednotky: [ν] = 1 / c = 1 s ^-1 = 1 Hz.

Porovnáváme vzorce pro úhlovou rychlost a rychlost otáčení, získáme výraz vztahující se k těmto veličinám:

ω = 2.

Hlavní prvky kinematiky nerovnoměrného rotačního pohybu

Nerovnoměrný rotační pohyb pevného nebo materiálového bodu kolem pevné osy charakterizuje jeho úhlovou rychlost, která se mění s časem.

Vektor ε , který charakterizuje rychlost změny úhlové rychlosti, se nazývá vektor úhlového zrychlení:

ε = dω / dt.

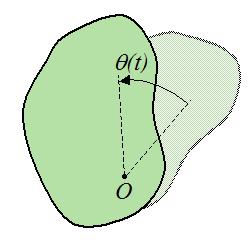
Pokud se tělo otáčí, urychluje, to znamená dω / dt> 0 , vektor má směr podél osy ve stejném směru jako ω.

Pokud je rotační pohyb pomalý - dω / dt <0 , jsou vektory ε a ω opačně směrovány.

Poznámka Když nastane nerovnoměrný rotační pohyb, vektor ω se může měnit nejen v rozsahu, ale i ve směru (když se rotační osa otáčí).

Vztah veličin charakterizujících translační a rotační pohyb

Je známo, že délka oblouku s úhlem natočení poloměru a jeho hodnotou souvisí

ΔS = Δφ r.

Pak lineární rychlost materiálu bodu vykonávat rotační pohyb

u = ΔS / Δt = Δφr / Δt = ωr.

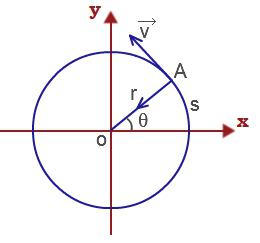
Normální zrychlení materiálu, které rotuje pohyb vpřed definujeme následovně:

a = υ ² / r = ω ² r ² / r.

Takže ve skalární podobě

a = ω ² r.

Tangenciální zrychlený bod materiálu, který provádí rotační pohyb

a = ε r.

Moment hybnosti materiálu

Vektorový produkt vektoru poloměru trajektorie hmotného bodu hmoty m _i jeho hybností se nazývá úhlová hybnost tohoto bodu vzhledem k ose rotace. Směr vektoru lze určit pravidlem pravého šroubu.

Moment hybnosti bodu materiálu ( L _i ) směřuje kolmo k rovině natočené r _i a _{i i} a vytvoří s sebou tři pravé vektory (tj. Při pohybu z konce vektoru r _i na _{i i} pravý šroub ukazuje směr vektoru L _i ).

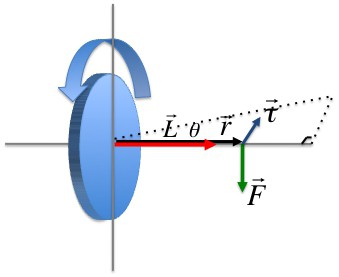
Ve skalární podobě

L = m _{i i i} r _i sin (υ _{i ,} r _i ).

Vzhledem k tomu, že při pohybu v kruhu jsou vektor poloměru a lineární vektor rychlosti pro i-tý materiálový bod vzájemně kolmé,

sin (υ _{i ,} r _i ) = 1.

Takže úhlová hybnost bodu materiálu pro rotační pohyb bude mít podobu

L = m _{i i i i i .}

Moment síly působící na i-tý materiálový bod

Vektorový produkt vektoru poloměru, který se udržuje v místě působení síly, touto silou se nazývá moment síly působící na i-tý materiálový bod vzhledem k ose rotace.

Ve skalární podobě

M _i = r _i F _i sin (r _i , F _i ).

Za předpokladu, že r _i sinα = l _i , Mi _i = l _i F _i .

Hodnota l _i rovnající se délce kolmice, snížené od bodu otáčení ke směru síly, se nazývá rameno síly F _i .

Dynamika rotace

Rovnice dynamiky rotačního pohybu je psána jako:

M = dL / dt.

Znění zákona je následující: rychlost změny momentu hybnosti těla, která se otáčí kolem pevné osy, se rovná výslednému momentu kolem této osy všech vnějších sil aplikovaných na tělo.

Moment impulsu a okamžiku setrvačnosti

Je známo, že pro i-tý materiálový bod je úhlová hybnost ve skalární podobě daná vzorecem

L _i = m _{i i i i i .}

Pokud namísto lineární rychlosti nahradíme jeho výraz úhlovým:

_{i i} = ωr _i ,

pak výraz pro momentální hybnost má formu

L _i = m _i r _i ² ω.

Množství I _i = m _i r _i ² se nazývá moment setrvačnosti kolem osy i-tého bodu materiálu absolutně tuhého tělesa procházejícího jeho středem hmoty. Pak se uvádí úhlová hybnost hmotného bodu:

L _i = I _i ω.

Moment impulsu absolutně tuhého těla je psán jako součet impulzních momentů hmotných bodů, které tvoří toto tělo:

L = Iω.

Moment síly a moment setrvačnosti

Zákon rotačního pohybu zní následovně:

M = dL / dt.

Známý představuje okamžik tělový impuls možné v okamžiku setrvačnosti:

L = Iω.

Pak

M = Id / dt.

Vzhledem k tomu, že úhlové zrychlení je určeno výrazem

ε = dω / dt,

získáme vzorec pro okamžik síly reprezentovaný okamžikem setrvačnosti:

M = Iε.

Poznámka Moment síly se považuje za pozitivní, jestliže je úhlové zrychlení, které je způsobeno, větší než nula a naopak.

Steinerova věta. Zákon přidání okamžiků setrvačnosti

Pokud je osa otáčení těla skrz centrum hmoty to neprojde, pak vzhledem k této ose najdete jeho moment setrvačnosti podle Steinerovy věty:
I = _I0 + ma ² ,

kde I ₀ - počáteční moment setrvačnosti těla; m je tělesná hmotnost; a je vzdálenost mezi osami.

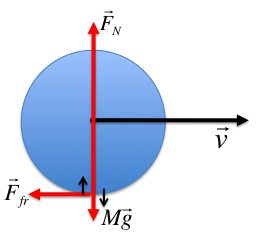
Pokud se systém, který se točí okolo pevné osy, skládá z n těl, pak se celkový moment setrvačnosti tohoto typu systému rovná součtu momentů, které to činí (zákon přidání momentů setrvačnosti).