Projekce bodu na rovině. Projekce bodu na přímce v rovině
Studium vlastností obrazců v prostoru a v rovině je nemožné bez znalosti vzdáleností mezi bodem a takovými geometrickými objekty jako přímka a rovina. V tomto článku ukážeme, jak tyto vzdálenosti zjistit s ohledem na projekci bodu v rovině a na přímce.
Rovnice řádku pro dvourozměrné a trojrozměrné prostory
Výpočet vzdáleností bodu na přímku a rovinu se provádí pomocí projekce na tyto objekty. Abychom mohli tyto projekce najít, měli bychom vědět, v jaké formě jsou rovnice pro přímky a roviny dány. Začněme první.
Přímka je sbírka bodů, z nichž každá může být získána z předchozího přesunu do paralelních vektorů. Například existuje bod M a N. Vektor MN¯, který je spojuje, má M na N. Existuje také třetí bod P. Pokud je vektor MP¯ nebo NP¯ rovnobûsný s MN¯, pak se nacházejí v ‰ echny tři body na jedné ãásti a vytvofií ji.
V závislosti na rozměru prostoru může rovnice definovat čáru změnit svůj tvar. Známá lineární závislost y souřadnice na x v prostoru tedy popisuje rovinu, která je rovnoběžná se třetí osou z. V tomto ohledu budeme v tomto článku brát v úvahu pouze vektorovou rovnici pro linii. Má stejný vzhled pro rovinu a trojrozměrný prostor.
V prostoru může být přímka definována následujícím výrazem:
(x, y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Hodnoty souřadnic s nulovými indexy odpovídají přímce, která patří k určitému bodu, u (a; b; c) jsou souřadnice vektoru, který leží na dané přímce, α je libovolné reálné číslo, měnící se můžete všemi body přímky. Tato rovnice se nazývá vektor.
Často je výše uvedená rovnice napsána v otevřené podobě:
x = x 0 + α * a;
y = y0 + α * b;
z = z0 + α * c
Podobně můžeme napsat rovnici pro přímku v rovině, tedy v dvourozměrném prostoru:
(x; y) = (x 0 ; y 0 ) + α * (a; b);
x = x 0 + α * a;
y = y 0 + α * b
Rovnice roviny
Abyste mohli najít vzdálenost od bodu k rovinám projekcí, potřebujete vědět, jak je definována rovina. Stejně jako přímka, může být zastoupena několika způsoby. Zde uvažujeme pouze jednu: obecnou rovnici.
Předpokládejme, že bod M (x 0 ; y 0 ; z 0 ) patří k rovině a vektor n ¯ (A; B; C) je kolmý k ní, pak pro všechny body (x; y; z) roviny platí následující rovnost:
A * x + B * y + C * z + D = 0, kde D = -1 * (A * x 0 + B * y 0 + C * z 0 )
Je třeba si uvědomit, že v této obecné rovnici roviny jsou koeficienty A, B a C souřadnicemi normálu k rovině vektoru.
Výpočet vzdáleností souřadnicemi
Předtím, než začneme zvažovat projekce v rovině bodu a na přímce, je třeba připomenout, jak by měla být vypočtena vzdálenost mezi dvěma známými body.
Předpokládejme, že existují dva prostorové body:
A 1 (x 1 ; y 1 ; z 1 ) a A 2 (x 2 ; y 2 ; z 2 )
Vzdálenost mezi nimi se vypočte podle vzorce:
A 1 A 2 = √ (((x 2- x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 )
Pomocí tohoto výrazu je také určena délka vektoru A 1 A 2 ¯.
Pro případ v rovině, kdy jsou dva body uvedeny pouze dvojicí souřadnic, můžete napsat podobnou rovnici bez přítomnosti člena se z ním:
A 1 A 2 = √ (((x 2- x 1 ) 2 + (y 2 -y 1 ) 2 )
Nyní budeme zvažovat různé případy projekce na rovině bodu na přímce a na rovině ve vesmíru.
Bod, řádek a vzdálenost mezi nimi
Předpokládejme, že existuje nějaký bod a přímka:
P 2 (x 1 ; y 1 );
(x, y) = (x 0 ; y 0 ) + α * (a; b)
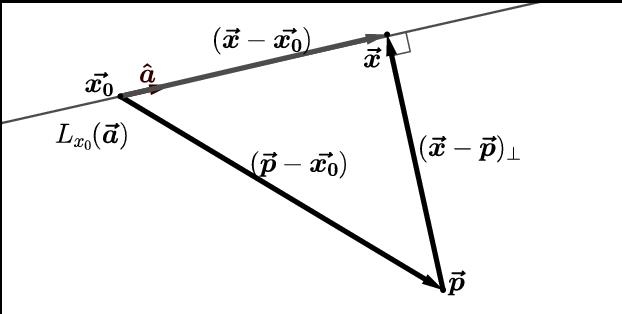
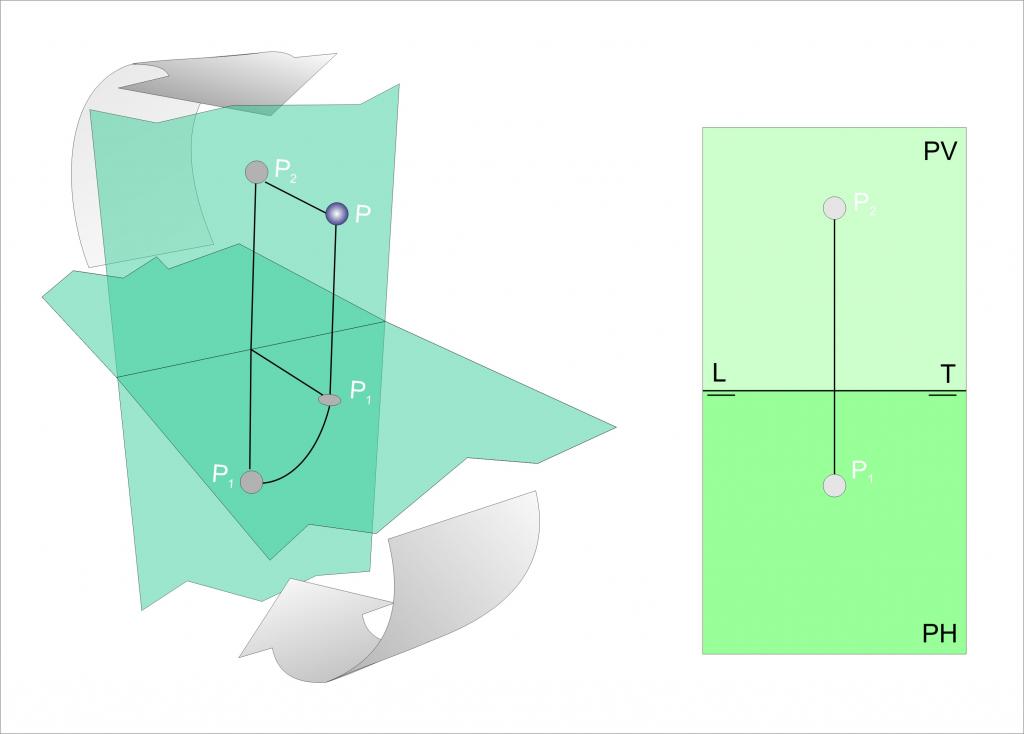
Vzdálenost mezi těmito geometrickými objekty bude odpovídat délce vektoru, jejíž počátek leží v bodě P 2 a konec je v takovém bodě P na uvedené přímce, přičemž vektor P 2 P ¯ této přímky je kolmý. Bod P se nazývá projekce bodu P 2 na dotyčné čáře.
Níže uvedený obrázek ukazuje bod P 2 , jeho vzdálenost d k přímce a také směrný vektor v 1 ¯. Také na linii je zvolen libovolný bod P 1 a od něj je odvozen vektor do P2. Bod P se shoduje s místem, kde kolmost protíná přímku.
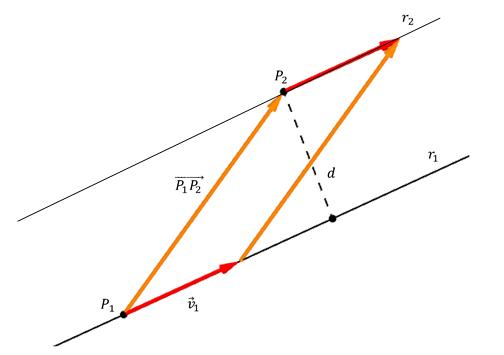
Je vidět, že oranžové a červené šipky tvoří rovnoběžník, jehož strany jsou vektor P 1 P 2 ¯ a v 1 ¯ a výška je d. Z geometrie je známo, že pro nalezení výšky paralelogramu by měla být jeho plocha rozdělena délkou základny, na níž je kolmice snížena. Vzhledem k tomu, že plocha rovnoběžníku je vypočítána jako vektorový produkt jeho stran, získáváme vzorec pro výpočet d:
d = | [P 1 P 2 ¯ * v 1 ¯] | / | v 1 ¯ |
Všechny vektory a souřadnice bodů v tomto výrazu jsou známy, takže je můžete použít bez provedení jakýchkoliv transformací.
Tento problém by bylo možné vyřešit jinak. Chcete-li to provést, zapište dvě rovnice:
- skalární produkt P 2 P ¯ on v 1 ¯ by měl být rovný nule, protože tyto vektory jsou vzájemně kolmé;
- souřadnice bodu P musí splňovat rovnici řádku.
Tyto rovnice stačí najít koordináty P a potom délku d podle vzorce uvedeného v předchozím odstavci.
Úloha zjištění vzdálenosti mezi čarou a bodem
Ukážeme, jak tyto teoretické informace použít k řešení konkrétního problému. Předpokládejme, že jsou známy následující body a řádky:
M (5; -3);
(x, y) = (3; 1) - α * (0; 2)
Je nutné nalézt body projekce na rovinu v rovině, stejně jako vzdálenost od M k přímce.
Označte projekci, která má být nalezena bodem M 1 (x 1 ; y 1 ). Tento problém řešíme dvěma způsoby popsanými v předchozím odstavci.
Metoda 1. Souřadnice směrového vektoru v 1 ¯ má (0; 2). Chcete-li vytvořit rovnoběžník, zvolte bod, který patří k přímce. Například bod se souřadnicemi (3; 1). Pak bude vektor druhé strany paralelogramu mít souřadnice:
(5; -3) - (3; 1) = (2; -4)
Nyní je nutné vypočítat produkt vektorů definujících strany rovnoběžníku:
[(2; -4) * (0; 2)] = 4
Nahrazujeme tuto hodnotu do vzorce, získáme vzdálenost d od M k přímce:
d = 4 / √4 = 2
Metoda 2. Teď najdeme jiným způsobem nejen vzdálenost, ale také souřadnice projekce M na linii, jak to vyžaduje stav problému. Jak bylo uvedeno výše, pro řešení problému je nutné vytvořit systém rovnic. Vypadá jako:
(x 1 - 5) * 0 + (y 1 +3) * 2 = 0;
(x 1 ; y 1 ) = (3; 1) -α * (0; 2)
Řešíme tento systém:
y1 = -3;
x 1 = 3
Projekce počátečního bodu souřadnice je M 1 (3; -3). Potom je požadovaná vzdálenost:
d = | MM 1 ¯ | = √ (4 + 0) = 2
Jak vidíte, obě řešení poskytly stejný výsledek, což ukazuje správnost provedených matematických operací.
Projekce bodu na rovině
Nyní zvažte, jaký je projekce bodu daného ve vesmíru v určité rovině. Je snadné si uvědomit, že tato projekce je také bod, který spolu s původním vytváří vektor kolmý k rovině.
Předpokládejme, že projekce v rovině bodů M má následující souřadnice:
M 1 (x 1 ; y 1 ; z 1 )
Samotná rovina je popsána rovnicí:
A * x + B * y + C * z + D = 0
Na základě těchto údajů můžeme vytvořit rovnici přímky protínající rovinu v pravém úhlu a procházející M a M 1 :
(x, y; z) = (x 0 ; y 0 ; z 0 ) + α * (A; B; C)
Zde proměnné s nulovými indexy jsou souřadnice bodu M. Je možné vypočítat polohu v rovině bodu M 1 za předpokladu, že její souřadnice musí splňovat obě písemné rovnice. Pokud tyto rovnice nejsou dostatečné k řešení problému, pak může být použita podmínka rovnoběžnosti MM 1 ¯ a směrového vektoru pro danou rovinu.
Je zřejmé, že projekce bodu, který patří do roviny, se shoduje s sebou a odpovídající vzdálenost je nula.
Úloha s bodem a rovinou
Nechť daný bod M (1; -1, 3) a rovina, která je popsána následující obecnou rovnicí:
-x + 3 * y-2 * z + 4 = 0
Je nutné vypočítat souřadnice projekce v rovině bodu a vypočítat vzdálenost mezi těmito geometrickými objekty.
Začneme tím, že budeme vytvářet rovnici čáry procházející M a kolmo k uvedené rovině. Vypadá to takto:
(x, y; z) = (1; -1; 3) + α * (- 1; 3;
Označte bod, kde tato přímka protíná rovinu M 1 . Rovnosti pro rovinu a přímku musí být splněny, pokud v nich nahrazujeme souřadnice M 1 . Napsáním explicitní rovnice rovnice získáváme následující čtyři rovnice:
-x 1 + 3 * y 1 -2 * z 1 + 4 = 0;
x 1 = 1 - α;
y 1 = -1 + 3 * a;
z 1 = 3 - 2 * α
Z poslední rovnosti získáme parametr α, pak jej nahradíme v předposledním a druhém výrazu, dostaneme:
α = (3-z1) / 2;
y 1 = -1 + 3 * (3-z 1 ) / 2 = -3 / 2 * z 1 + 3,5;
x 1 = 1 - (3-z 1 ) / 2 = 1/2 * z 1 - 1/2
Výraz pro y 1 a x 1 je nahrazen rovnicí pro rovinu, máme:
-1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3,5) -2 * z 1 + 4 = 0
Kde se dostaneme:
z 1 = 15/7
Pak:
y 1 = -3 / 2 * 15/7 + 3,5 = 2/7;
x 1 = 1/2 * 15/7 - 1/2 = 4/7
Zjistili jsme, že projekce bodu M na dané rovině odpovídá souřadnicím (4/7; 2/7; 15/7).
Nyní vypočteme vzdálenost | MM 1 ¯ | Souřadnice odpovídajícího vektoru jsou:
MM 1 ¯ (-3/7; 9/7; -6/7)
Požadovaná vzdálenost je:
d = | MM 1 ¯ | = √126 / 7 ≈ 1,6
Tři projekční body
Během výroby výkresů je často nutné získat výčnělky úseků na vzájemně kolmých třech rovinách. Proto je užitečné zvážit, jaké projekce určitého bodu M se souřadnicemi (x 0 ; y 0 ; z 0 ) na tři souřadnice budou rovny.

Není obtížné dokázat, že rovina xy je popsána rovnicí z = 0, rovina xz odpovídá výrazu y = 0 a zbývající rovina yz je označena rovnicí x = 0. Je snadné odhadnout, že projekce bodu na 3 rovinách budou stejné:
pro x = 0: (0; y 0 ; z 0 );
pro y = 0: (x 0 ; 0; z 0 );
pro z = 0: (x 0 ; y 0 ; 0)
Kde je důležité znát projekce bodu a jeho vzdálenost k rovinám?
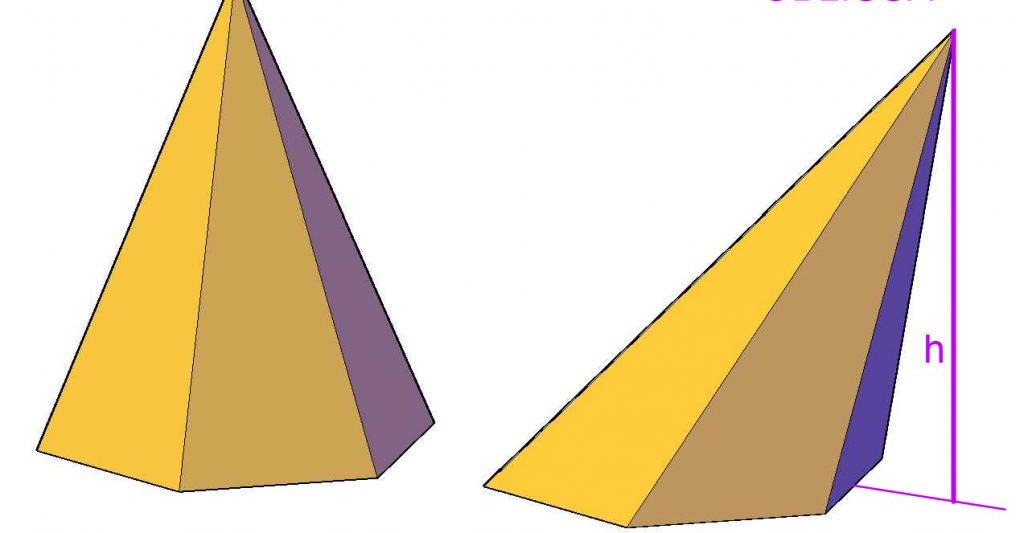
Určení polohy projekce bodů v dané rovině je důležité, když se objeví takové veličiny jako plocha a objem pro šikmé hranoly a pyramidy. Například vzdálenost od vrcholu pyramidy k rovině základny je výška. Druhý je zahrnut ve vzorci pro objem tohoto čísla.
Zvažované vzorce a metody pro určení výčnělků a vzdáleností od bodu k přímce a rovině jsou poměrně jednoduché. Je důležité pouze zapamatovat si odpovídající formy roviny a přímé rovnice a také mít dobrou prostorovou představivost, aby bylo možné je úspěšně aplikovat.