Jaký je index lomu skla? A kdy je nutné vědět?

Při řešení problémů v optice je často nutné znát index lomu skla, vody nebo jiné látky. V různých situacích mohou být zahrnuty jak absolutní, tak relativní hodnoty této hodnoty.

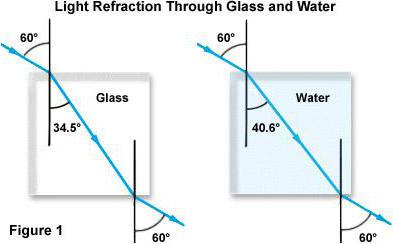
Dva druhy indexu lomu

Za prvé, skutečnost, že toto číslo ukazuje: jak toto nebo toto průhledné médium mění směr šíření světla. A elektromagnetická vlna může pocházet z podtlaku a index lomu skla nebo jiné látky bude nazván absolutní. Ve většině případů je jeho hodnota v rozmezí od 1 do 2. Pouze ve velmi vzácných případech je index lomu větší než dva.

Pokud je před subjektem hustší prostředí než vakuum, pak již hovoří o relativní hodnotě. A je vypočítán jako poměr dvou absolutních hodnot. Například relativní index lomu vodní sklo se bude rovnat konkrétním absolutním hodnotám pro sklo a vodu.

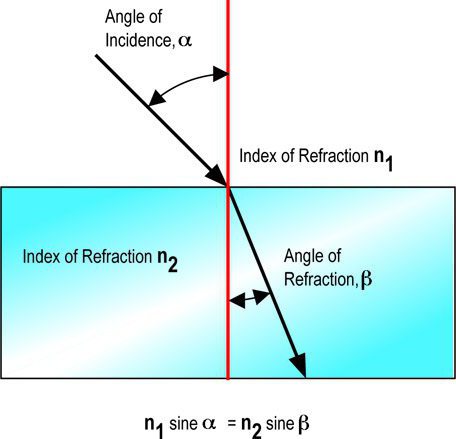
V každém případě je označen latinkou "en" - n. Tato hodnota se získá vzájemným dělením se stejnou hodnotou, proto je to jednoduše koeficient, který nemá žádné jméno.

Jaký vzorec lze použít k výpočtu indexu lomu?

Pokud považujeme úhel dopadu za "alfa" a úhel lomu je označen jako "beta", vzorec pro absolutní hodnotu indexu lomu vypadá takto: n = sin α / sin β. V literatuře anglického jazyka můžete často najít jiné označení. Pokud je úhel dopadu i a lom je r.

Existuje další vzorec pro výpočet indexu lomu světla ve skle a jiných průhledných médiích. Je spojena s rychlostí světla ve vakuu a tím, že je již ve zkoumané látce.

Pak vypadá takto: n = c / νλ. Zde c je rychlost osvětlení ve vakuu, ν je jeho rychlost v průhledném médiu a λ je vlnová délka.

Co určuje index lomu?

Určuje se rychlostí, kterou světlo prochází v uváděném médiu. Vzduch v tomto ohledu je velmi blízký vakuu, proto se světlá vlny v něm šíří prakticky neodchylují od svého původního směru. Proto, jestliže je určen index lomu skleněného vzduchu nebo jakékoliv jiné látky sousedící se vzduchem, potom se tento obvykle považuje za vakuum.

Každé jiné médium má své vlastní vlastnosti. Mají různé hustoty, mají svou vlastní teplotu, stejně jako elastické napětí. To vše ovlivňuje výsledek refrakce světla podle hmoty.

Ne poslední roli při změně směru šíření vln hrají vlastnosti světla. Bílé světlo se skládá z různých barev, od červené až fialové. Každá část spektra je lámána svým vlastním způsobem. Navíc hodnota indexu pro vlnu červené části spektra bude vždy nižší než zbytek. Například index lomu skla TF-1 se pohybuje od 1,6421 do 1,67298 od červené až po fialovou část spektra.

Příklady hodnot pro různé látky

Zde jsou hodnoty absolutních hodnot, tj. Indexu lomu, když paprsek prochází z vakua (která se rovná vzduchu) přes jinou látku.

Tyto údaje se budou vyžadovat, pokud je nutné určit index lomu skla vzhledem k jiným médiím.

Jaké další hodnoty se používají při řešení problémů?

Plný odraz. Je pozorováno, když světlo prochází od hustšího média k méně husté. Zde se při určitém úhlu dopadu objevuje lom v pravém úhlu. To znamená, že paprsek klouže podél hranice dvou médií.

Maximální úhel celkového odrazu je jeho minimální hodnota, při níž světlo nevstupuje do méně hustého média. Méně než to - dochází k refrakci a ještě více - odraz ve stejném prostředí, ze kterého se světlo pohybovalo.

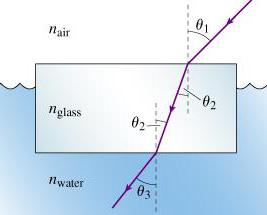
Číslo problému 1

Stav Index lomu skla je 1,52. Je nutné stanovit omezující úhel, kterým se světlo z rozhraní mezi plochami zcela odráží: sklo se vzduchem, voda se vzduchem, sklo s vodou.

Rozhodnutí.

Budete muset použít tento index lomu pro vodu uvedený v tabulce. Je to pro vzduch, který se rovná jednomu.

Řešení ve všech třech případech je redukováno na výpočty podle vzorce:

sin α ₀ / sin β = n ₁ / n ₂ , kde n _{2 se} vztahuje na médium, ze kterého se světlo šíří, a n _1, kde proniká.

Písmeno α ₀ označuje mezní úhel. Hodnota úhlu β je 90 stupňů. To znamená, že jeho sinus bude jedna.

Pro první případ: sin α ₀ = 1 / n _sklo , potom je hraniční úhel roven arcinu 1 / n _skla . 1 / 1,52 = 0,6579. Úhel je 41,14 °.

Ve druhém případě je při určování arcsine nutné nahradit hodnotu indexu refrakce vody. Poměr 1 / n _vody bude mít hodnotu 1 / 1,33 = 0, 7519. Toto je úhel oblouku 48,75 °.

Třetí případ je popsán poměrem n _vody a n _skla . Arcsine bude muset vypočítat zlomek 1,33 / 1,52, tj. Číslo 0,875. Najděte hodnotu omezovacího úhlu podle jeho oblouku: 61,05 °.

Odpověď: 41,14 °, 48,75 °, 61,05 °.

Číslo problému 2

Stav Skleněný hranol je ponořen do nádoby vodou. Jeho index lomu je 1,5. Prism je založen na pravý trojúhelník. Větší noha je kolmá na dno a druhá je rovnoběžná s ní. Světelný paprsek dopadá normálně na horní plochu hranolu. Jaký by měl být nejmenší úhel mezi vodorovnou nohou a hypotenzou, aby světlo dosáhlo nohy, která je kolmá ke spodní části nádoby a vyjde z hranolu?

Rozhodnutí.

Aby mohl paprsek vystupovat z hranolu popsaným způsobem, musí spadnout na krajní hranu v extrémním úhlu (ten je hypotenzou trojúhelníku v řezu hranolu). Tento mezní úhel se rovná požadovanému úhlu pravoúhlého trojúhelníku. Ze zákona refrakce světla se ukazuje, že sinus omezujícího úhlu děleného sínusem o 90 stupňů se rovná poměru dvou indexů lomu: voda na sklo.

Výpočty vedou k této hodnotě pro omezovací úhel: 62 ° 30 '.

Odpověď: 62 ° 30 '.