Aritmetická progrese - číselná sekvence
Někdo je ostražitý pojem "progrese" jako velmi komplikovaný termín ze sekcí vyšší matematiky. Zatím nejjednodušší aritmetický postup je práce taxi (kde stále zůstává). A pochopit podstatu (a v matematice není nic důležitějšího než "pochopit podstatu") aritmetické posloupnosti není tak obtížné, protože pochopil několik elementárních pojmů.
Sekvence matematických čísel
Číselná sekvence se obvykle nazývá sérií čísel, z nichž každá má své vlastní číslo.
a 1 - první člen sekvence;
a 2 - druhý člen sekvence;
...
a 7 - sedmý člen sekvence;
...
a n je n-tý člen sekvence;
Nic nás ovšem neznamená žádná libovolná množina čísel a čísel. Naše pozornost bude zaměřena na číselnou sekvenci, ve které hodnota n-tého termínu souvisí s jeho pořadovým číslem vztahem, který lze jasně vyjádřit matematicky. Jinými slovy: číselná hodnota n-tého čísla je funkcí n.
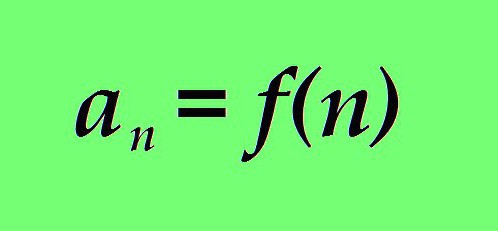
kde:
a je hodnota člena číselné sekvence;
n je jeho pořadové číslo;
f (n) je funkce, kde sekvenční číslo v číselné sekvenci n je argument.
Definice
Aritmetická progrese se nazývá číselná sekvence, ve které je každý následující pojem (méně) než předchozí po stejném čísle. Vzorec pro nth termín aritmetické sekvence je následující:
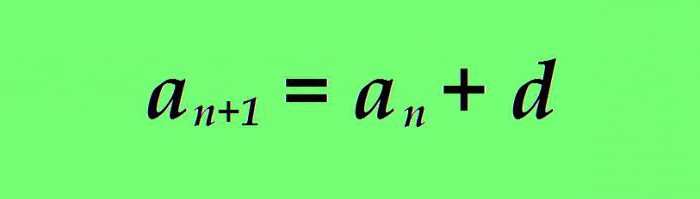
kde
a n - hodnota aktuálního člena aritmetické progrese;
a n + 1 je vzorec pro další číslo;
d - rozdíl (určité číslo).
Je snadné zjistit, že je-li rozdíl kladný (d> 0), pak každý následující člen sledujícího souboru bude větší než předchozí a takový aritmetický postup se bude zvyšovat.
Příklad:
a 1 = 5
d = 3
pak
číslo člena - n | 1 | 2 | 3 | 4 | 5 | 6 |
hodnota člena - a n | 5 | 8 | 11 | 14 | 17 | 20 |
V níže uvedeném grafu není těžké vysledovat, proč se číselná sekvence nazývá "zvyšováním".
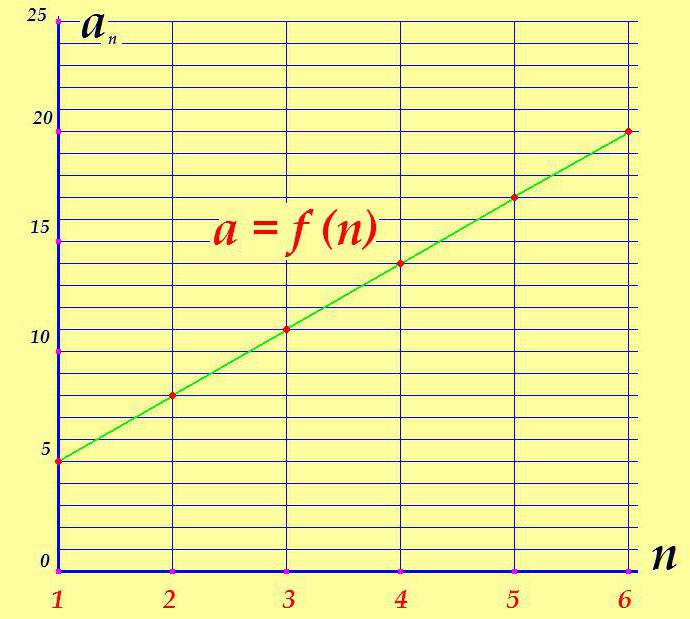
V případech, kdy je rozdíl záporný (d <0), bude každý z následujících členů ze zřejmých důvodů menší než předchozí, graf postupu bude "dolů" dolů, aritmetická progrese bude respektována jako klesající.
Hodnota zadaného člena
Někdy je nutné určit hodnotu jakéhokoli libovolného pojmu a n aritmetického postupu. Můžete to provést výpočtem hodnot všech členů aritmetické progrese, od prvního po požadovaný. Taková cesta však není vždy přijatelná, jestliže je například třeba najít hodnotu pětitisícové nebo osmi milionové členů. Tradiční výpočet bude trvat dlouho. Avšak určitá aritmetická progrese může být zkoumána pomocí určitých vzorců. Existuje také vzorec pro nth termín: hodnota každého člena aritmetické progrese může být určena jako součet prvního semestru progrese s rozdílem progrese vynásobeným počtem člena, který má být nalezen, snížen o jednu.
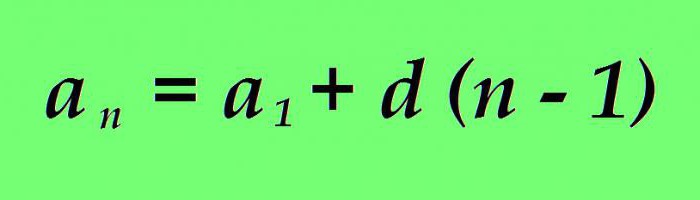
Vzorec je univerzální pro vzestupný a sestupný průběh.
Příklad výpočtu hodnoty daného člena
Vyřešíme následující problém nalezení hodnoty n-tého termínu aritmetické progrese.
Stav: existuje aritmetický postup s parametry:
- první termín sekvence je 3;
- rozdíl v číselné řadě je 1,2.
Úkol: je třeba najít hodnotu 214 členů
Řešení: pro určení hodnoty daného člena používáme vzorec:
a (n) = a1 + d (n-1)
Nahrazením výrazových dat z podmínek problému máme:
a (214) = a1 + d (n-1)
a (214) = 3 + 1,2 (214-1) = 258,6
Odpověď: 214. člen posloupnosti se rovná 258,6.
Výhody této metody výpočtu jsou zřejmé - celé řešení trvá ne více než 2 řádky.
Částka daného počtu členů
Velmi často se v dané aritmetické sérii vyžaduje určit součet hodnot určitého segmentu. K tomu není třeba vypočítávat hodnoty každého člena a pak shrnout. Tato metoda je použitelná, pokud je počet členů, jejichž částka se nachází, malá. V jiných případech je vhodnější použít následující vzorec.
Součet členů aritmetické progrese od 1 do n se rovná součtu prvního a n-tého členu vynásobeného číslem člena n a rozděleného do dvou. Pokud ve vzorci hodnota n-tého člena nahrazuje výraz z předchozího odstavce článku, získáme:
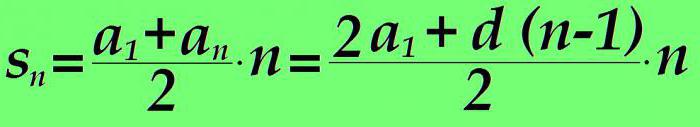
Příklad výpočtu
Například vyřešit problém s následujícími podmínkami:
- první termín sekvence je nulový;
- rozdíl je 0,5.
Úkolem je určit součet členů série od 56. do 101. ročníku.
Rozhodnutí. Používáme vzorec pro určení množství progrese:
s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2
Nejprve definujeme součet hodnot 101 členů progrese, nahrazující ve vzorci data o podmínkách naší úlohy
s 101 = (2 ∙ 0 + 0,5 ∙ (101-1)) ∙ 101/2 = 2 525
Je zřejmé, že pro zjištění součtu členů postupu z 56. na 101. místo je nutné odečíst S 55 od S 101 .
s 55 = (2 ∙ 0 + 0,5 ∙ (55-1)) ∙ 55/2 = 742,5
Součet aritmetické progrese pro tento příklad:
s 101 - s 55 = 2 525 - 742,5 = 1 782,5
Příklad praktické aplikace aritmetické progrese
Na konci článku se vrátíme k příkladu aritmetické sekvence uvedené v prvním odstavci - taxametru (počítadlo taxi). Zvažte tento příklad.
Přistání v taxíku (které zahrnuje 3 kilometry) stojí 50 rublů. Každý další kilometr se platí ve výši 22 rublů / km. Cestovní vzdálenost je 30 km. Vypočítejte cenu výletu.
1. Vyhoďte první 3 km, jehož cena je zahrnuta v ceně přistání.
30 - 3 = 27 km.
2. Další výpočet není nic jiného než analýza aritmetických číselných řad.
Číslo člena je počet ujetých kilometrů (minus první tři).
Hodnota člena je součet.
První termín v tomto problému bude rovný 1 = 50 p.
Rozdíl v postupu d = 22 p.
počet zájmů je hodnota (27 + 1) - člen aritmetické progrese - měření na konci 27. kilometru - 27,999 ... = 28 km.
a 28 = 50 + 22 ∙ (28 - 1) = 644
Formuláře popisující určité číselné sekvence se používají k výpočtu dat kalendáře pro libovolně dlouhé období. V astronomii je délka oběžné dráhy v geometrické závislosti na vzdálenosti nebeského těla od hvězdy. Kromě toho jsou úspěšně použity různé číselné řady ve statistikách a dalších aplikovaných oborech matematiky.
Další typ sekvence čísel je geometrický.
Geometrická progrese je charakterizována velkým, v porovnání s aritmetickým tempem změny. Není náhodou, že v politice, sociologii a medicíně se často říká, že proces se vyvíjí exponenciálně, aby ukázal vysokou míru šíření jevu, například onemocnění v epidemii.
Nth termín řady geometrických čísel se liší od předchozího čísla tím, že je vynásoben pevným číslem - jmenovatelem, například prvním termínem je 1, jmenovatelem je 2, resp.
n = 1: 1, 2 = 2
n = 2: 2, 2 = 4
n = 3: 4, 2 = 8
n = 4: 8; 2 = 16
n = 5: 16,2 = 32,
n = 6: 32 ∙ 2 = 64 a tak dále ...
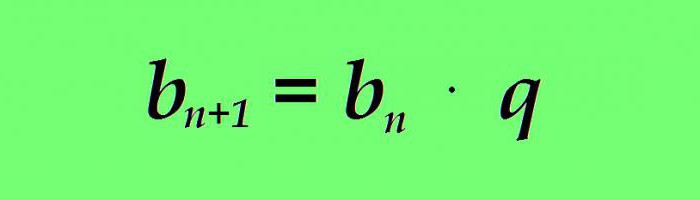
kde:
b n - hodnota současného termínu geometrické progrese;
b n + 1 - vzorec pro další termín geometrického postupu;
q je jmenovatel geometrického průběhu (konstantní číslo).
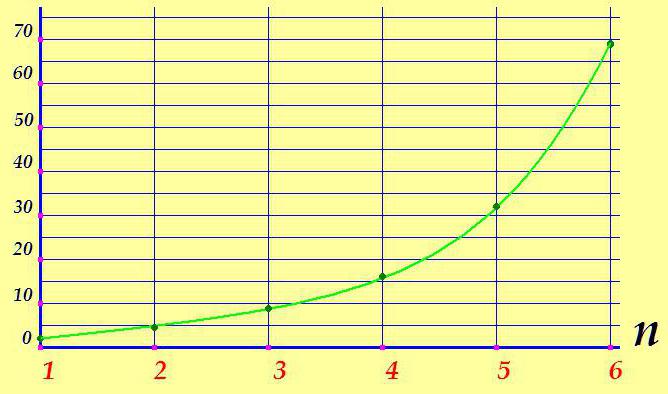
Pokud je graf aritmetické progrese přímka, pak geometrický nakreslí trochu jiný obrázek:
Stejně jako v případě aritmetiky má geometrický průběh vzorec pro hodnotu libovolného pojmu. Jakýkoli n-tý termín geometrického postupu se rovná součinu prvního termínu jmenovatelem postupu do stupně n sníženého o jeden:
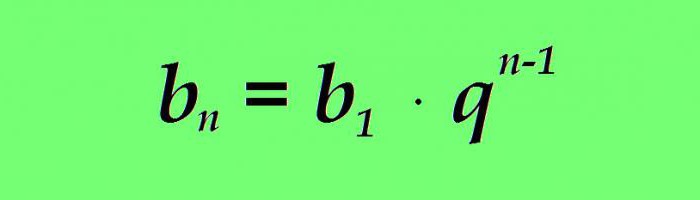
Příklad. Máme geometrický postup s prvním termínem rovným 3 a jmenovatelem progrese 1,5. Najděte 5. člen postupu
b 5 = b 1 ∙ q (5-1) = 3 ∙ 1,5 4 = 15,1875
Součet daného počtu členů se vypočítá také pomocí zvláštního vzorce. Součet n prvních termínů geometrického postupu se rovná rozdílu produktu n-tého termínu progrese jeho jmenovatelem a prvního termínu progrese děleného jmenovatelem sníženého o jeden:
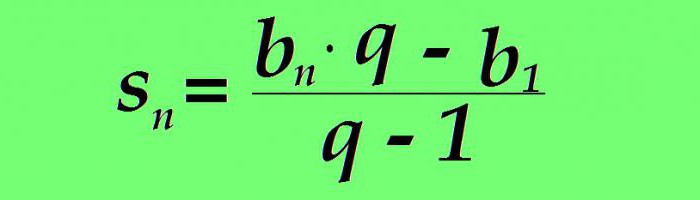
Je-li b n nahrazeno výše uvedeným vzorcem, hodnota součtu n prvních členů zvažované číselné řady má podobu:
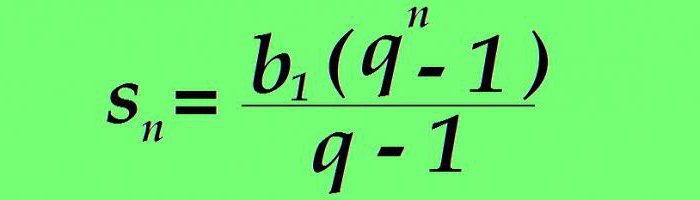
Příklad. Geometrická progrese začíná prvním termínem rovným 1. Denominátor je nastaven na 3. Najděte součet prvních osmi členů.
s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280