Combinatorics - co to je? Prvky kombinatoriky
Odborníci v různých oborech musí vyřešit kombinované problémy: přestavování čísel, značek a dalších objektů. Například vedoucí obchodu potřebuje rozdělit různé druhy práce mezi pracovní stroje. Kombinatorika je významná větev matematiky, která, jak to není těžké odhadnout, najde svou výbavu v různých oborech a oborech: fyzika, biologie, lingvistika, chemie, inženýrství, teorie kódování a mnoho dalšího. Zásady kombinatoriky jsou také základem řešení množiny pravděpodobnostních problémů.
Dějiny
První předpoklady kombinatoriky jako vědy se objevily v 16. století. Přispělo k rozvoji této oblasti znalostí do značné míry zájem lidí o hazardní hry: karty, kostky, loterie ztratily nejen zlato a šperky, ale paláce a panství. Přemýšlíte-li například o tom, jak často můžete házet dobré body na kosti nebo získat dvě esa, lidé se postupně dostali k základům kombinatoriky a pravděpodobnosti. Pomohlo kombinátorům, aby někdo vyhrál více nebo ztratil méně? Otázka je zajímavá, ale její úvaha je mimo rozsah tohoto článku.

První matematik, který se aktivně zajímal o kombinátory, byl italský italský Tartaglia (1499-1557), po němž se aktivně ponořili do studia těchto otázek významní vědci jako Pascal, Fermat, Bernoulli, Leibnitz, Euler a další. stále zůstala, ne-li zábavná hra s čísly, pak teorie, která se používá výhradně v hazardních hrách a nemá právo používat jinde.
Vývoj kombinatoriky
Významné pokroky v kombinaci se staly s příchodem 20. století. počítače, programování a především - diskrétní matematika. Během tohoto období se combinatorics dostane vrcholu rychlého vývoje a stane se plnohodnotnou vědou. Kombinatorické metody se začínají používat všude:
- řešení dopravních problémů;
- plánování;
- příprava plánů na výrobu a prodej zboží;
- v teorii náhodných procesů;
- v matematické statistice a teorii pravděpodobnosti;
- při přípravě a provádění experimentů;
- v šachu;
- v termodynamice;
- v geometrii;
- a v mnoha dalších oblastech.
Superstitious Leader Challenge
Na světě byl vůdce, který věřil, že číslo 8 mu přináší naprosté selhání. Proto se rozhodl zbavit se všech čísel, které obsahovaly číslo osm. Pod jeho dohledem pracovalo 600 lidí. Všichni měli identifikační číslo povolení k práci, skládající se ze tří čísel. Bez dvojnásobného přemýšlení se manažer rozhodl vyloučit číslo 8 z počtu průchodů a pak se zamyslel nad tím, zda existuje dostatečné množství čísel pro 600 osob z rozsahu od 000 do 999, které by zahrnovalo 8?
Samozřejmým řešením tohoto problému je ručně napsat všechny číslice od 000 do 999 a vyškrtnout ty, ve kterých je osm. Je možné vyřešit problém jednodušším způsobem? Pokud pro 999 čísel bude úkol s výčtem všech variant vypadat jako proveditelný, pak rozsah od 000000 do 999999 bude vyžadovat mnohem větší úsilí. Je to úspora času a úsilí navržených kombinatorik.
Řešení problému pověrčivého vůdce
Dalším řešením je následující. Odstraníme 8 z této série, máme 0, 1, 2, 3, 4, 5, 6, 7, 9 - tyto devět čísel jsou platné. Poté byste měli najít všechna dvoumístná čísla, která by neobsahovala 8. To se děje jednoduše: z platného čísla musíte přijmout libovolné číslo a přidat k němu libovolné číslo z platné. Tímto způsobem získáme všechna dvoumístná čísla, která odpovídají danému stavu. Výsledkem je, že každá jediná číslice poskytne 9 různých dvoumístných čísel. Celkový počet takových číslic bude 9 * 9 = 9 2 = 81.
Při pokračování analogie můžeme usoudit, že pro získání všech třímístných čísel bez osmičků je třeba přiřadit třetí číslice stávajícím dvoumístným číslům, také od povolených hodnot. Pak zjistíme, že počet takových čísel bude 9 2 * 9 = 9 * 9 * 9 = 729. Zjistili jsme tedy, že náš vedoucí ředitel by byl snadno schopen poskytnout 600 zaměstnancům mezery, které by neobsahovaly 8. Vyzkoušejte řešení problému pro sebe s pětimístnými čísly.
A co se stane, pokud se manažerovi nelíbí číslo 2? Ukazuje se, že počet přijatelných čísel bude 8, jmenovitě: 0, 1, 3, 4, 5, 6, 7, 9. Poté, když odhadujeme počet kombinací čísel bez 2 a 8, můžeme usuzovat, že jejich počet je 8 * 8 * 8 = 512, a to zjevně nestačí na to, aby poskytlo průchod 600 osobám. Kombinatorika je věda, která pomáhá zodpovědět takové otázky efektivněji, než je to možné pomocí brutálních sil.
Lotto problém
Každý ví hru. K dispozici je sáček, ve kterém se nacházejí sudy s čísly od 1 do 90. Vstupenky jsou rozdávány všem účastníkům, u kterých je nutno namalovat určitý počet buněk s čísly. Poté vedoucí lote dostane z tašky jeden z očíslovaných sudů. Vítězem bude ten, kdo překonal většinu čísel na lístku, což se shoduje s těmi, které hostitel hry vyskočil.

Jakmile Nina hraje lotto, pomyslela si. Často sledovala, jak se přednášející dostane z tašky stejného čísla. Ale zároveň se první dva sudy ukázaly být stejně méně často. Pak si uvědomila, kolik způsobů, jak si z vaku vytrhnout dva sudy? Prvky kombinatoriky pomáhají zodpovědět její otázku.
Lotto řešení
Je zřejmé, že první barel může mít čísla od 1 do 90. Jinými slovy, existuje 90 způsobů, jak získat první barel. Ale co dál? Pokud se například z tašky vyjme sudo č. 63, pak se v současné hře nestane znovu.
Metoda tabulky nám pomůže vyřešit tento problém. Tam, kde se v nadpisu a ve sloupci označí čísla sloupců od 1 do 90. Na průsečíku libovolné čáry a libovolného sloupce bude pár čísel nebo pár sudů vyjmutých z vaku. Ve stejné době na diagonále stolu budou umístěny stejné dvojice čísel. To je nemožné podle stavu, protože po vyjmutí jedné číslice z vaku je jeho opakování nemožné. Získat tabulku následujícího formuláře:
| 1 | 2 | ... | 90 | |
| 1 | x | 1, 2 | ... | 1, 90 |
| 2 | 2, 1 | x | ... | 2, 90 |
| ... | ... | ... | x | ... |
| 90 | 90, 1 | 90, 2 | ... | x |
Celkem máme tabulku, ve které je počet buněk 90 * 90 = 8100. Mělo by být zapamatováno, že na diagonále je 90 párů číslic, což není možné za daných podmínek. Poté odpověď na otázku, kolik způsobů získáte 2 barely z tašky bude 8100 - 90 = 8010 možností.
Odůvodňujte trochu jiným způsobem, jak můžete dosáhnout stejné odpovědi. Pro první hlaveň je 90 možností. Po prvním vyjmutí zůstane pro druhou hlaveň 89 možností. Celkový počet možností bude tedy 90 * 89 = 8010. Prvky kombinatoriky mohou být použity různými způsoby. Jedinou otázkou je jednoduchost a univerzálnost metody. Metoda tabulky může být například použita pro tři sudy, které mají být extrahovány v řadě, a samozřejmě to bude limit. A co pro čtyři nebo více?
Problém posádky
Pokud volby závisí na tom, které objekty byly vybrány dříve, je vhodné zobrazovat takový proces jako "strom". V prvním kroku je z jednoho bodu vytyčeno tolik řádků, jelikož v prvním kroku existují možnosti volby. Na konci každého řádku je také tolik dalších řádků, které lze provést ve druhém kroku atd. Výsledkem je, že se vytvoří druh stromu nebo grafu. Kombinatorika a teorie mohou znít poměrně matoucí a nepochopitelné, takže se podívejme na příklad.
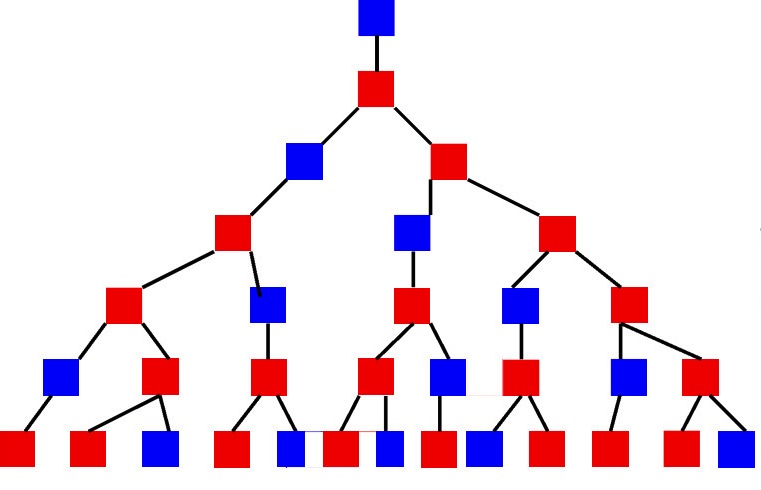
Před zahájením expedičního roku má vedení úkol - shromažďovat posádky na výlety. Každý tým musí zahrnovat tři osoby: velitele, inženýra a lékaře. Zároveň se počet odborníků v určité oblasti může lišit. Přípustné je například, že jeden lékař je poslán na dvě různé expedice, jelikož tam jsou jen dva lékaři, a tam mohou být tři v každém veliteli a inženýrovi. V tomto případě musí kompilátor expedičního plánu vzít v úvahu psychologickou kompatibilitu členů týmu. Tato charakteristika je jedním z nejdůležitějších v dlouhých a vzdálených expedicích pro jejich úspěšné chování. Na základě všech popsaných podmínek se objevuje následující obrázek:
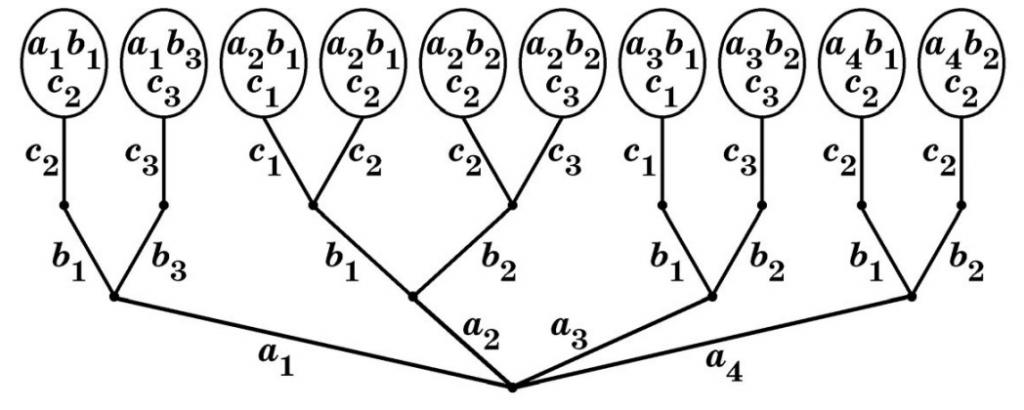
Kde já jsem velitelé, jsou to inženýři a já jsem doktoři. Současně se při zkouškách každé osoby zjistilo, že velitel a psychologicky se dobře setká s inženýry b 1 a b 3 , a 2 - s b 1 a b 2 , ale doktor c 3 je neslučitelný s inženýrem b 1 atd. Otázkou, která byla původně položena manažerovi projektu, bylo, kolik posádek lze sestavit za takových podmínek. Z grafu lze vidět, že celkově může jít o deset takových posádek. Ale co by se stalo, kdyby otázka psychologické kompatibility neměla váhu? Pak se ukáže, že po výběru velitelů a i , by bylo pro každý z nich 3 alternativy ve výběru inženýra. V případě dvojice velitelů a inženýrů by pro lékaře existovaly také tři možnosti. Pak počet kombinací dosáhne 4 * 3 * 3 = 36 posádek.
Umístění, permutace a kombinace
Ve výše uvedených příkladech se řešení problémů vyskytlo tzv. Axiomatickou metodou. To znamená, že lze říci, že existuje řada základních úkolů, jejichž řešení lze omezit na řadu problémů. Stejně jako ve stereometrii je však nepohodlné vyřešit problémy založené výhradně na axiomy a pro tento účel se používá vhodnější nástroj nazvaný "věty", takže v kombinatoricích je vhodnější používat obecnější a osvědčené metody. V průběhu staletí studie kombinátorů bylo zřejmé, že řada úkolů se setkává častěji než jiné a byly rozděleny do samostatných tříd a jejich jména se staly hlavními kombinatorikami - jmenovitě umístěními, permutacemi a kombinacemi.

Kombinatorické problémy
Jedním z klíčových problémů kombinačních metod je určení toho, který soubor úkolů by měl být považován za kombinační. To nemůže být přesně definováno kvůli extrémně širokému spektru problémů, které spadají do kombinační kategorie. A pak se spousta úkolů může týkat kombinatorik, stejně jako do jiné oblasti, která je sousedící nebo hraniční.

Ve zjednodušeném případě lze poznamenat, že kombinatorická matematika zahrnuje problémy zahrnující vzorky a umístění objektů. Současně se kombinátory vyznačují tím, že pracují výhradně s konečnou sadou objektů. Na základě těchto ustanovení můžeme rozlišit následující úkoly charakteristické pro kombinátory:
- Vytvořte výběr objektů s přihlédnutím k jakýmkoli vlastnostem.
- Prokázat nebo vyvrátit existenci vzorku za určitých podmínek.
- Najděte počet možných kombinací.
- Najděte všechny kombinace a určete algoritmus jejich výčtu.
- Najděte optimální řešení problému za daných podmínek.
Pokud je daný problém přiřazen jednomu z těchto typů, pak je kombinatorický a kombinační vzorce pomohou mu vyřešit.