Typ dat: pole. Je to jednoduché a elegantní.

Při programování se člověk často setkává s datovými typy, jako jsou pole. Toto je nejjednodušší řešení při provádění podobných operací s velkým počtem proměnných stejného typu. Pokud se pokusíte napsat program, který bude obsahovat všechna tato data a opakované výpočty, je vhodnější zahrnout do produktu strukturu nazvanou pole nebo matici.

Obecná koncepce polí

Pod matricí (někteří je jednodušší ji prezentovat ve formě tabulky) se rozumí sekvence paměťových buněk, ve kterých jsou uloženy proměnné stejného typu. V tomto případě se vztah mezi daty a strukturou provádí jedním jménem a zadaným indexem. Pomáhá určit, kterou proměnnou je třeba použít při řešení problému.

Mělo by být zřejmé, že index není obsahem buňky. Poukazuje pouze na data obsažená v konkrétní buňce.

Definice takové struktury bude následující: pole jsou skupinou dat stejného typu, které mají své vlastní jméno a ukládají proměnné do po sobě jdoucích paměťových buněk.

Existují dva typy matic: jednorozměrná (lineární) struktura a dvojrozměrné pole. První typ je prezentován ve formě tabulky s pouze jedním řádkem nebo jedním sloupcem. V konkrétním případě počet indexů udává velikost matice.

Dvojrozměrné pole je struktura reprezentovaná jako tabulka, ve které číslo řádku označuje první index a číslo sloupce označuje druhou. Takže v matici A (m, n) prvek pole a ₂₃ ukazuje, že tato proměnná je ve druhém řádku av třetím sloupci. A m udává počet řádků a n - počet sloupců. K dispozici je čtvercová matice (kde je počet řádků a sloupců stejný) a obdélníkový.

Pole v programování

Již jsme zjistili, že pole jsou sbírkou prvků stejného typu. A typ dat musí být v tabulce stejné. Každá struktura může mít úplně jiný datový typ: číselný, řetězec, znak.

Při psaní programu můžete nastavit hranice dvěma způsoby:

• pomocí názvu typu, kde první a poslední hodnota je oddělovač;
• s použitím dříve deklarovaných konstant.

Struktura může být také definována několika způsoby. Rád bych poznamenal, že každý programový jazyk má svou vlastní syntaxi. Princip vytváření matice je však podobný. V prvním případě je vyvolán určitý prvek pomocí názvu proměnné struktury a indexu v hranatých závorkách. V jiném případě může být matice specifikována pouze uvedením všech prvků.

Nezaměňujte pojmy "index" a "typ indexu". První definice je uvedena v sekci výkazu, aby bylo možné určit konkrétní prvek pole. A typ indexu se používá pouze v části popisu struktury. Rozměr pole je uveden v popisu. Je velmi nežádoucí měnit počet prvků v procesu práce na programu.

Matrice s daty v programování můžete vyplnit následujícími způsoby:

• pomocí ručního zadávání klávesnice;
• pomocí generátoru náhodných čísel;
• při deklarování pole jako konstanty;
• daným vzorem.

Strukturování pole

Políčka jsou strukturovaný datový typ. Jak již bylo uvedeno, matice (pokud je dvourozměrná) sestává z konečného počtu řádků a sloupců; pokud je lineární, je z jednoho řádku nebo jednoho sloupce, kde je počet prvků také omezen.

Průsečík řádku a sloupce se nazývá buňka. Obsahuje specifické proměnné. V jedné tabulce není povoleno mít různé typy dat. Prvky pole jsou proměnné s indexy (bez ohledu na to, zda je struktura lineární nebo dvourozměrná). Index je číslo určité buňky. Označuje její postavení v tabulce.

Operace pole: Přidání

Takže datové pole, které v matematice, které je v informatice, je množinou proměnných. Můžete s ní provádět různé operace: sčítání, odečítání, transpozice, násobení, dělení.

Při přidání je nutné vzít v úvahu skutečnost, že rozměr obou struktur by měl být stejný. V tomto případě, jsou-li matice A a B uvedeny s rozměrem MxN, pak ve výsledných prvcích C = A + B bude c [i, j] = a [i, j] + b [i, j]. Ukazuje se, že proměnné jsou přidávány elementárně.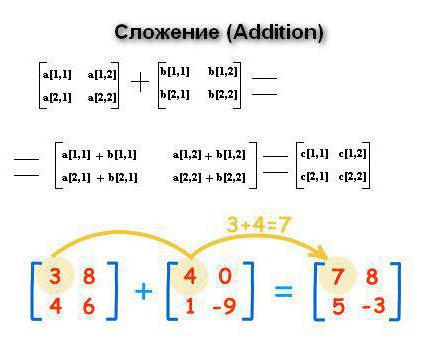

Operace pole: odčítání

Tento bod by se měl začít nejprve odstraněním znaménka mínus z matice (nebo naopak, úvodem). Existují případy, kdy se datová pole skládá z prvků, většina z nich je záporná. V takové situaci by bylo lepší přesunout mínus ze struktury. K tomu je umístěno záporné znaménko před tabulkou a každý prvek má své znamení obrácené. Zero v tomto případě je neutrální: nemá žádné kladné nebo záporné znaménko.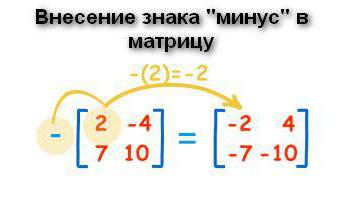

Odčítání se provádí na stejném principu jako přidání. Proměnná se stejným indexem z jiné struktury je odečtena od prvního maticového prvku. Odpověď je zaznamenána ve třetí tabulce na odpovídající pozici.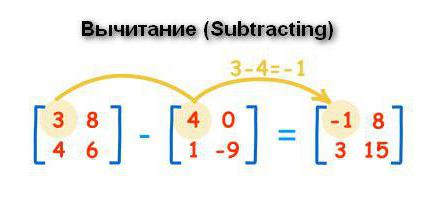

Operace pole: násobení a rozdělení

Kromě sčítání a odčítání lze množinu čísel vynásobit číslem, vynásobit dvě struktury dohromady, rozdělit jeden po druhém.

Chcete-li najít produkt matice a číslo, je nutné vynásobit každý prvek matice zadaným prvkem. Odpověď je zaznamenána v buňce se stejným indexem jako původní proměnná. 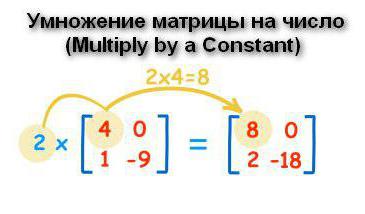Chcete-li vynásobit dvě matice navzájem, je nutné dodržovat následující algoritmus.

• Počet sloupců v první tabulce se rovná počtu řádků druhého násobitele. V takovém případě bude rozměr výsledné matice následující: počet řádků se bude rovnat počtu řádků prvního faktoru a počet sloupců se bude rovnat jejich počtu od druhého faktoru.

• Zvažte dva faktory.

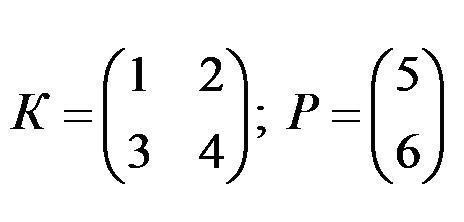
• Vzhledem k tomu, že počet sloupců ve faktoru K se rovná počtu řádků v poli P, je operace možná. Ale pokud vyměníte matice v místech, pak zákon o změně míst multiplikátorů zde nefunguje. Proto je P x ​​K neplatný záznam. Pokud jsou obě matice čtvercové, operace je možná v obou případech.

Násobící vzorec je následující.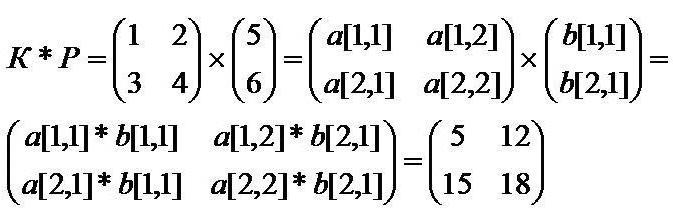

Pokud jsou oba faktory dvourozměrné, je třeba dodržovat princip uvedený na následujícím obrázku.

Dělení se provádí podle následujícího vzorce. 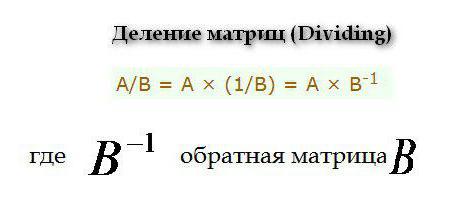Pokud se objeví inverzní matice (inverzní), provede se podle následujícího vzorce.

Transpozice

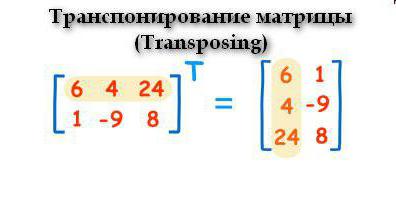
Tato operace se provádí podle následujícího principu: řádky se stávají sloupci. Vypadá to takhle.