Stanovení momentu hybnosti, síly a setrvačnosti. Momentová rovnice Příklad řešení problému

Dynamika rotace je jednou z důležitých úseků moderní mechaniky, která zvažuje zákony rotačního pohybu těles kolem os a bodů. V tomto článku budeme podrobně studovat hlavní rovnici dynamiky rotace - rovnice momentů.

Moment impulsu

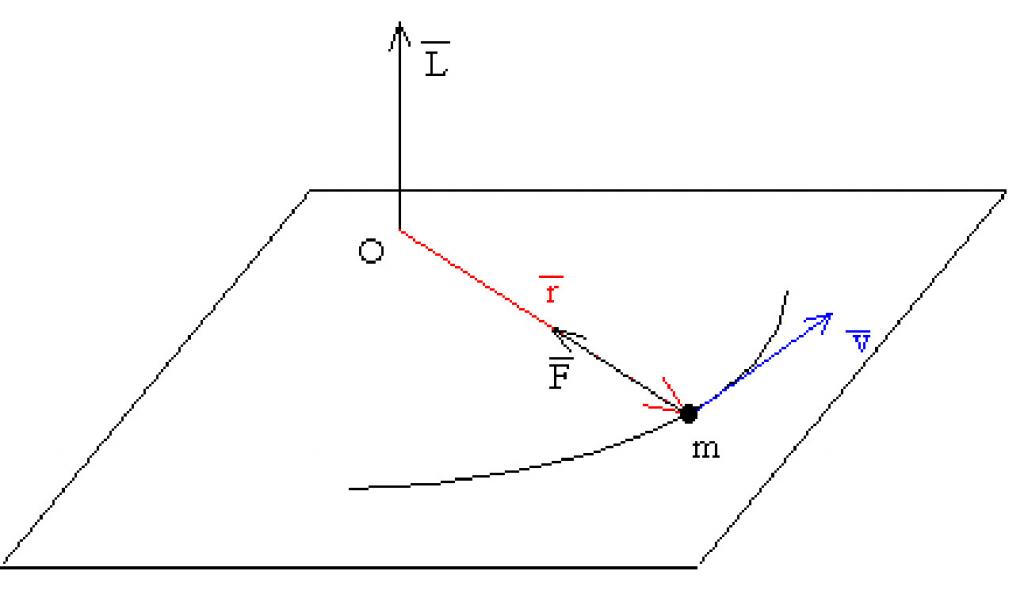
Každý školák vědí, co představuje mechanický impuls, který se správně nazývá mírou pohybu. Teď předpokládejme, že materiálový bod s hmotností m se otáčí kolem osy O lineární rychlostí v. Pokud je poloměr rotace označen jako r, pak můžeme napsat následující výraz:

L¯ = [m * v¯ * r¯].

První dva faktory na pravé straně rovnosti jsou lineární hybnost bodu. Produkt tohoto impulsu vektorem r¯, směřujícím od osy otáčení k bodu, se nazývá moment hybnosti L¯.

Hodnota L¯ je vektor. Je směrována kolmo k rovině otáčení bodu. Směr hybnosti hybnosti bodu materiálu se určuje pravidlem pravítka nebo pravidlem gimlet. Otáčením bodu proti směru hodinových ručiček vytvoříte kladný moment hybnosti.

Vzhledem k tomu, že rychlost otáčení v¯ je směrována tangenciálně k kruhové dráze, vektorový výraz může být přepsán ve skalární podobě:

L = m * v * r.

Moment síly

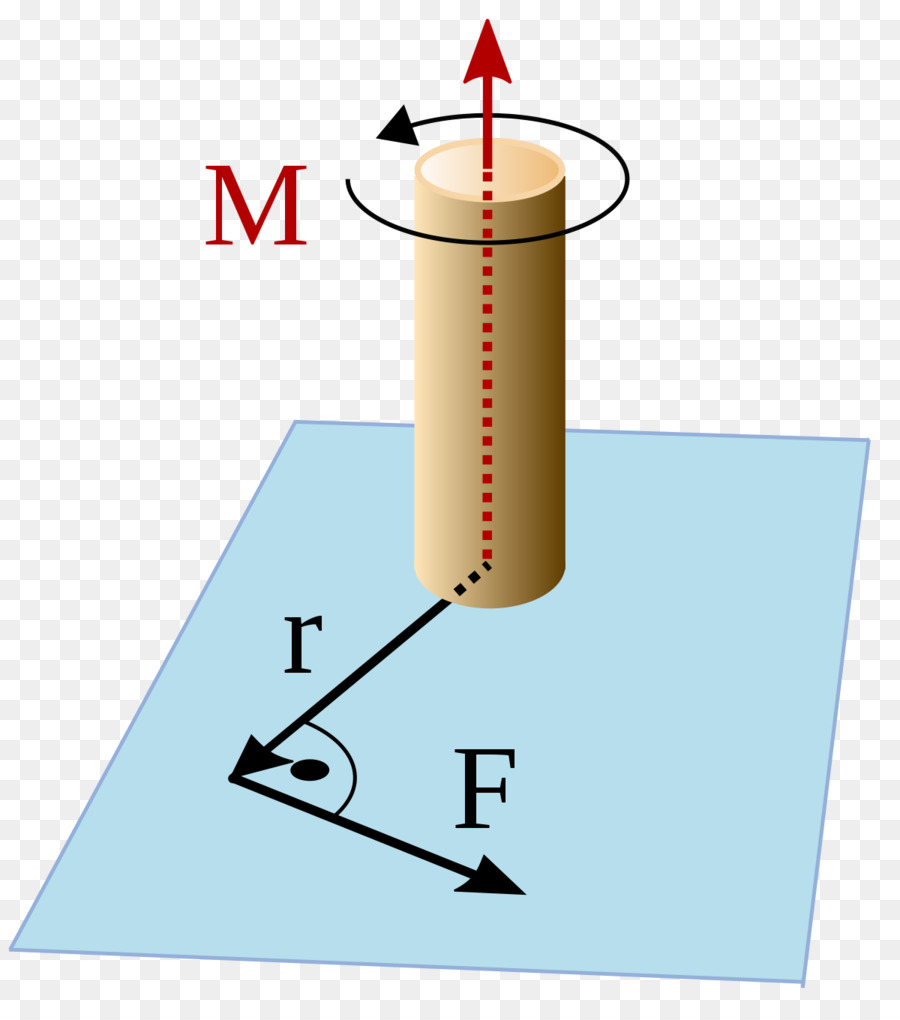
To je další důležitá vlastnost rotačního pohybu. Ve fyzice se toto množství zavádí stejným způsobem jako úhlová hybnost hmotného bodu, ale namísto množství pohybu bychom měli nahradit tangenciální sílu ve výše uvedeném vzorci. Máme:

M¯ = [r¯ * F¯].

Moment síly, který se také nazývá momentem točivého momentu, charakterizuje jeho schopnost obrátit systém a dát jí úhlové zrychlení.

Směr vektoru točivého momentu M¯ je určen stejnými pravidly jako pro vektor L¯. Pokud systém provede zrychlené natočení, pak M¯ a L¯ se shodují ve směru, pokud se zpomalí, pak budou opačně nasměrovány.

Pokud je síla F ¯ a radius-vektor r-будут vzájemně kolmá, pak vektorová forma záznamu se změní na podobný skalární:

M = r * F.

Hodnota r se nazývá pákou síly. Čím větší je jeho hodnota, tím větší je síla F, a tím větší bude úhlové zrychlení systému.

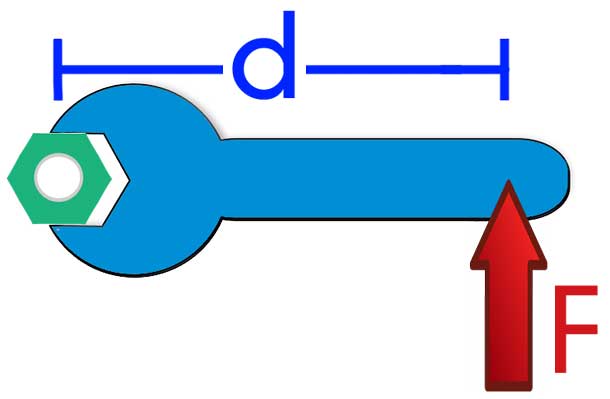
Příklady, které umožňují jasnější představu o fyzickém významu M¯, odšroubují matici speciálním dlouhým klíčem, proces otevírání dveří tlakem v blízkosti držadla a poblíž závěsů dveří, stejně jako proces držení těla určité hmotnosti na těle, táhnuté a přitlačené k tělu rameno.

Moment setrvačnosti

Zbývá definovat třetí bod, který se používá pro kvantitativní popis procesu rotace. Moment setrvačnosti bodu materiálu, jehož parametry byly zaznamenány na začátku článku, se vypočítá podle vzorce:

I = m * r ² .

Na rozdíl od ostatních dvou okamžiků (M¯ a L¯) je moment setrvačnosti skalární. Pomocí této funkce jsou popsány inerciální vlastnosti systému (analogie s hmotností při translačním pohybu).

Je zřejmé, že pro určení hodnoty I pro pevný těleso složitého tvaru a nejednotné hustoty byste měli používat integrální číslo:

I = ∫ _m (r ² * dm).

Ve skutečnosti vzorec odráží součet množství I _i pro každý materiálový bod i.

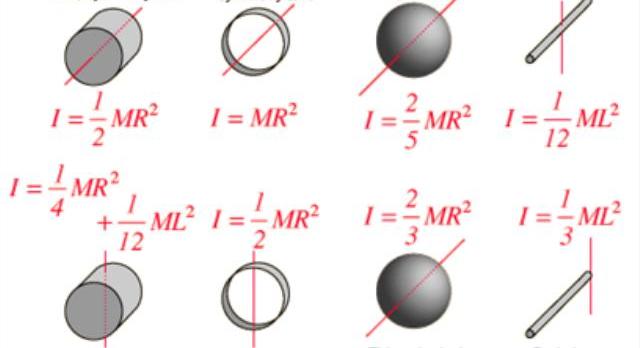
Moment setrvačnosti I je charakteristický nejen tvaru a rozložení hmotnosti v systému rotace, ale také závisí na umístění osy. Například mnozí si všimli, že je mnohem snazší otáčet kovovou tyč nebo dřevěný mop po osách procházejících jejich délkou než podél kolmé osy. Ve druhém případě má moment setrvačnosti větší význam.

Momentová rovnice pro materiálový bod

Nyní je čas jít přímo na téma článku. Pokud moment M působí po dobu dt, vede to ke změně momentu hybnosti o dL, to znamená:

dL = M * dt.

Tato rovnost je rozdílnou formou psaní momentové rovnice ve fyzice. Převeďte termín dt na levou stranu rovnosti a přepište dL explicitně:

dL / dt = M =>

m * dv * r / dt = M.

Připomeňme si, že lineární rychlost v kinematice souvisí s úhlovou rovnicí:

v = ω * r.

Nahrazením do rovnice okamžiků získáme:

m * dω * r ² / dt = M =>

I * α = M, kde α = dω / dt, I = m * r ² .

Získaná rovnost se často používá k určení kinematických vlastností rotujícího systému, jsou-li známy okamžik vnějších sil M a okamžik setrvačnosti I.

Zákon o zachování hodnoty

Momentová rovnice ukazuje, jak se moment hybnosti změní, když působí vnější moment M. Co se stane se systémem, pokud se M ukáže být nulou? V tomto případě bude hodnota L uložena. Matematický vzorec pro tuto situaci je napsán následovně:

L = const nebo

L = m * r * v = m * r ² * ω = I * ω = const.

Všimněte si, že podmínka M = 0 by měla být splněna pouze pro vnější síly. Vnitřní síly, které vytvářejí okamžik M, nemohou měnit moment hybnosti systému.

Zákon o zachování L se používá pro střídání umělých družic ve vesmíru a krasování. Takže seskupením různými způsoby mění sportovec hodnotu jeho momentu setrvačnosti, což vede k proporcionální změně rychlosti jeho úhlové rotace.

Příklady úkolů

Síla 10 N působí na hmotný bod o hmotnosti 2 kg. Vědomí, že poloměr otáčení bodového materiálu kolem osy je 0,5 m, a také vzhledem k tomu, že síla působí tangenciálně na trajektorii, je nutné najít úhlovou rychlost bodu 5 sekund po zahájení pohybu .

Napíšeme rovnici okamžiku a vyjádříme zrychlení α:

I * α = M =>

α = M / I.

Nyní nahrazujeme výrazy M a já, s přihlédnutím k podmínkám problému, máme:

α = F * r / (m * r ² ) = F / (m * r).

Protože zvažovaný pohyb nastane s konstantním zrychlením α, bude pro výpočet ω:

ω = α * t.

Nahrazením výsledného vyjádření pro α získáme konečný pracovní vzorec:

ω = F * t / (m * r).

Vzhledem k datům problému můžete napsat odpověď: ω = 50 rad / s. Tato hodnota odpovídá téměř 8 otáček kolem osy za sekundu.