Frakce - co to je? Typy zlomků

Studium královny všech věd - matematiky, v určitém okamžiku každý čelí frakcím. Přestože je tento pojem (stejně jako typy zlomků nebo matematické operace s nimi) je poměrně jednoduchý, mělo by se s ním zacházet opatrně, protože v reálném životě mimo školu to bude velmi užitečné. Takže si osvěžte své znalosti o frakcích: co je to, co je to, jaké jsou tam a jak provádět různé aritmetické operace s nimi.

Fragment jejího veličenstva: Co je to?

Frakce v matematice jsou čísla, z nichž každá sestává z jedné nebo více částí jednotky. Takové frakce se také nazývají obyčejné nebo jednoduché frakce. Zpravidla jsou napsány ve formě dvou čísel, které jsou odděleny vodorovnou nebo lomítkovou čárou, nazývá se "frakční". Například: ½, ¾.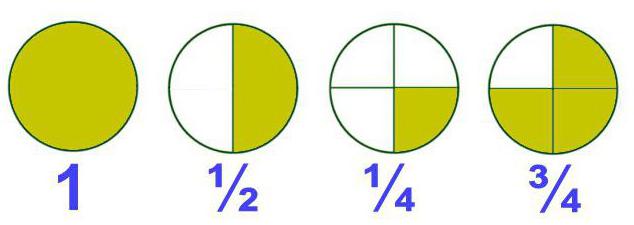

Horní nebo první z těchto čísel je čitatel (udává, kolik frakcí je odebíráno od čísla) a dolní nebo druhá je jmenovatel (ukazuje, kolik jednotek je rozděleno do jednoho).

Frakční sloupec skutečně vykonává funkci oddělovací značky. Například 7: 9 = 7/9

Tradičně jsou běžné zlomky méně než jeden. Zatímco desetinná místa mohou být větší než její.

Proč jsou frakce? Ano, pro všechno, protože ve skutečném světě, ne všechna čísla jsou celá čísla. Například dvě školky v jídelně koupily v kabelce jednu lahodnou čokoládu. Když se chystají sdílet dezert, setkali se s přítelkyní a rozhodli se s ní a jí. Nicméně nyní je nutné řádně rozdělit čokoládovou tyčinku, pokud se domníváme, že se skládá z 12 malých čtverců.

Nejprve dívky chtěly rozdělit vše rovnoměrně a pak dostaly čtyři kusy. Ale když to přemýšleli, rozhodli se zacházet s přítelkyní, ne s 1/3, ale s 1/4 čokoládou. A protože žákyně špatně zkoumaly zlomky, nezohlednily, že v takovém případě by měly 9 kusů, které jsou velmi špatně rozděleny na dvě. Tento poměrně jednoduchý příklad ukazuje, jak důležité je najít správnou část čísla. Ale v životě jsou takové případy mnohem víc.

Typy zlomků: obyčejné a desítkové

Všechny matematické zlomky jsou rozděleny na dvě velké číslice: obyčejné a desítkové. Zvláštnosti prvního z nich byly diskutovány v předchozím odstavci, takže nyní stojí za to věnovat pozornost druhému.

Desetinná tečka je polohová položka zlomku čísla, která je pevně připevněna na písmeno oddělené čárkami, bez pomlčky nebo lomítka. Například: 0,75, 0,5.

Ve skutečnosti je desetinná zlomek totožná s obyčejnou, avšak v jejím jmenovateli je vždy jeden, po němž následují nuly - odtud její název.

Číslo před čárkou je celočíselná část a všechno po ní je zlomkové. Jakékoliv jednoduché zlomky lze převést na desetinnou čárku Tedy desetinné zlomky uvedené v předchozím příkladu lze psát jako obyčejné: ¾ a ½.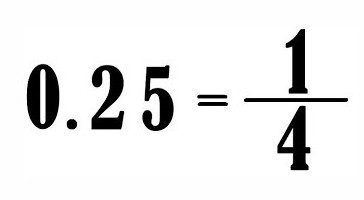

Za zmínku stojí, že jak desítkové, tak obyčejné frakce mohou být pozitivní i negativní. Pokud jim předchází znaménko "-", je tato zlomka negativní, pokud je "+" kladná.

Podsítě běžných frakcí

Existují takové druhy zlomků jednoduché.

• Správně. Mají hodnotu čitatele vždy nižší než jmenovatel. Například: 7/8. To je správný zlomek, protože čitatel 7 je menší než jmenovatel 8.
• Špatně. V takových zlomcích se čitatel a jmenovatel vzájemně rovnají (8/8) nebo nižší hodnota čísla je menší než horní číslo (9/8).
• Smíšené Toto je název správného zlomku napsaného s celočíselným číslem: 8 ½. Chápe se jako součet tohoto počtu a zlomků. Mimochodem, můžete jednoduše učinit, aby se na jeho místě objevila špatná zlomka. Chcete-li to provést, 8 musí být napsáno jako 16/2 + 1/2 = 17/2.
• Sloučenina. Jak vyplývá z názvu, sestávají z několika částí: ½ / ¾.
• Snížená / neredukovatelná. Mohou obsahovat jak správné, tak nesprávné zlomky. Vše závisí na tom, zda čitatel a jmenovatel lze rozdělit na stejné číslo. Například, 6/9 je snížená zlomek, protože obě jeho složky mohou být děleny třemi a dostanete 2/3. Ale 7/9 odkazuje na neredukovatelné, protože 7 a 9 jsou primární čísla, která nemají společného dělitele a nemohou být redukována.

Podspeciy desetinná místa

Na rozdíl od jednoduchých desetinných zlomků se dělí pouze na dva typy.

• Finále - dostal své jméno kvůli skutečnosti, že za čárkou má omezený (konečný) počet číslic: 19,25.
• Nekonečná zlomek je číslo s nekonečným počtem desetinných míst. Pokud například rozdělíte 10 na 3, výsledek bude nekonečný zlomek 3 333 ...

Frakce

Je trochu obtížnější provést různé aritmetické manipulace s frakcemi než s běžnými čísly. Pokud se však naučíte základní pravidla, vyřešit nějaký příklad s nimi nebude těžké.

Abyste si mezi sebou přidali zlomky, musíte si nejprve ujistit, že oba termíny mají stejné jmenovatele. K tomu je nutné najít nejmenší číslo, které lze sdílet bez vyvážení jmenovatelů dodatkových čísel.

Například: 2/3 + 3/4. Nejmenší společný násobek pro ně bude 12, proto je nutné, aby každý jmenovatel obsahoval toto číslo. Z tohoto důvodu se čitatel a jmenovatel prvního zlomku vynásobí 4, ukáže se 8/12, postupujeme stejným způsobem s druhým semestrem, ale pouze násobíme o 3 - 9/12. Nyní můžete snadno vyřešit příklad: 8/12 + 9/12 = 17/12. Výsledná zlomek je nesprávná hodnota, protože čitatel je větší než jmenovatel. Může a musí být přeměněn na správnou smíšenou, dělící 17: 12 = 1 a 5/12.

Pokud jsou přidány smíšené frakce, nejprve se provedou akce s celistvými a pak s dílčími.

Pokud příklad obsahuje desetinné a obyčejné zlomky, je nezbytné, aby se oba staly jednoduchými, poté je přiveďte ke stejnému jmenovateli a přidejte je. Například 3.1 + 1/2. Číslo 3.1 může být napsáno jako smíšený zlomek 3 a 1/10 nebo jako nesprávný zlomek - 31/10. Společný jmenovatel pro addendy je 10, takže musíte vynásobit čitatel a jmenovatele 1/2 až 5 střídavě, což je 5/10. Pak můžete snadno vypočítat všechno: 31/10 + 5/10 = 35/10. Získaný výsledek je neredukovatelný snížený zlomek, přivedeme jej do normální podoby, redukujeme o 5: 7/2 = 3 a 1/2, nebo desetinné - 3.5.

Pokud přidáte 2 desetinná místa, Je důležité, aby desetinná tečka byla stejný počet číslic. Pokud tomu tak není, stačí přidat požadovaný počet nul, protože v desítkovém případě to lze provést bez vážných následků. Například 3,5 + 3,005. Chcete-li tento úkol vyřešit, musíte přidat první číslo dvěma nulami a přidat jednu po druhé: 3 500 + 3 005 = 3 505.

Odčítání frakcí

Po odečtení zlomku byste měli postupovat stejně jako při přidání: snížit na společného jmenovatele, odečíst jeden čitatel od druhého, v případě potřeby překládat výsledek do smíšené frakce.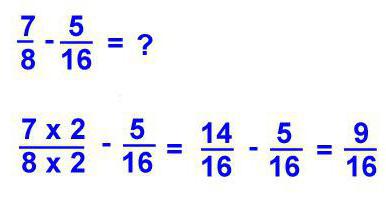

Například: 16 / 20-5 / 10. Společným jmenovatelem bude 20. Je nutné přenést druhou frakci na tento jmenovatel, vynásobením oběma jeho částmi dvěma, to ukazuje 10/20. Nyní můžeme vyřešit příklad: 16 / 20-10 / 20 = 6/20. Tento výsledek se však týká redukovatelných frakcí, takže je vhodné rozdělit obě části na 2 a výsledek je 3/10.

Násobení frakcí

Rozdělení a násobení frakcí jsou mnohem jednodušší operace než sčítání a odečítání. Faktem je, že při plnění těchto úkolů není třeba hledat společného jmenovatele.

Chcete-li násobit zlomky, stačí střídavě vynásobit mezi sebou jak čitatelé, tak i oba jmenovatele. Výsledný výsledek se sníží, jestliže je frakce snížená.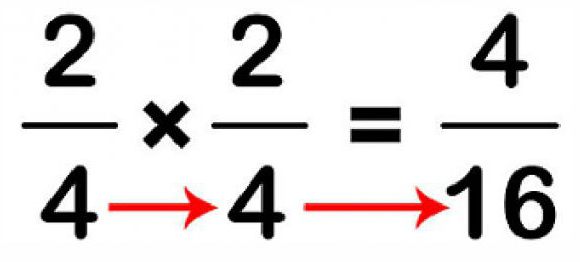

Například: 4 / 9x5 / 8. Po alternativním násobení získáme výsledek 4x5 / 9x8 = 20/72. Taková frakce je snížena o 4, takže konečná odpověď v příkladu je 5/18.

Jak rozdělit zlomky

Rozdělení frakcí je také nekomplikovaná akce, ve skutečnosti to všechno snižuje jejich násobení. Chcete-li rozdělit jednu zlomek o druhou, je třeba obrátit druhou a vynásobit ji druhou.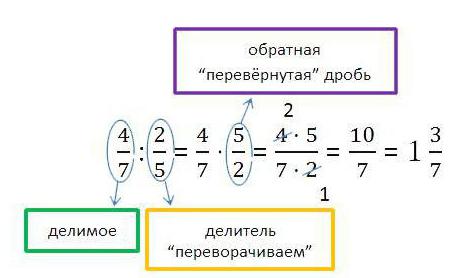

Například rozdělení frakcí 5/19 a 5/7. Chcete-li vyřešit příklad, musíte vyměnit jmenovatel a čitatel druhého zlomku a vynásobit: 5 / 19x7 / 5 = 35/95. Výsledek lze snížit o 5 - to se ukáže 7/19.

V případě, že je třeba rozdělit zlomek na primární číslo, je metoda mírně odlišná. Zpočátku je nutné zapsat toto číslo jako nesprávný zlomek a poté rozdělit podle stejného schématu. Například 2/13: 5 by měl být napsán jako 2/13: 5/1. Nyní musíte otočit 5/1 a násobit výslednou frakci: 2 / 13x1 / 5 = 2/65.

Někdy je nutné rozdělit frakce smíšené. Musí to dělat stejně jako s celistvými čísly nesprávné zlomky otočte dělič a vynásobte vše. Například 8 ½: 3. Vše obrácujeme na nepravidelné frakce: 17/2: 3/1. Následuje následuje obrat 3/1 a násobení: 17 / 2x1 / 3 = 17/6. Nyní je nutné přeložit nesprávný zlomek do správného zlomku - 2 celé a 5/6.

Takže, když jste pochopili, jaké frakce jsou a jak můžete s nimi provádět různé aritmetické operace, měli byste se o to pokusit zapomenout. Koneckonců, lidé jsou vždy více nakloněni rozdělit něco na části než přidat, takže musíte být schopni to udělat správně.