Jak vytvořit graf lineární funkce. Příklady
Abychom zjistili, jak vykreslovat lineární funkci, je důležité pochopit samotnou podstatu funkce. Funkce je model závislosti změn jednoho parametru na jiný.
Téma funkčních závislostí je tradičně otevřena s lineární funkční závislostí. Lineární je nejjednodušší závislost. Graf lineární funkce je přímý.
Život a funkce
V životě se lineární závislosti obvykle nacházejí v ideálních umělých procesech, jejichž změny se považují za trvalé. Například, když člověk někam jde s konstantní rychlostí.
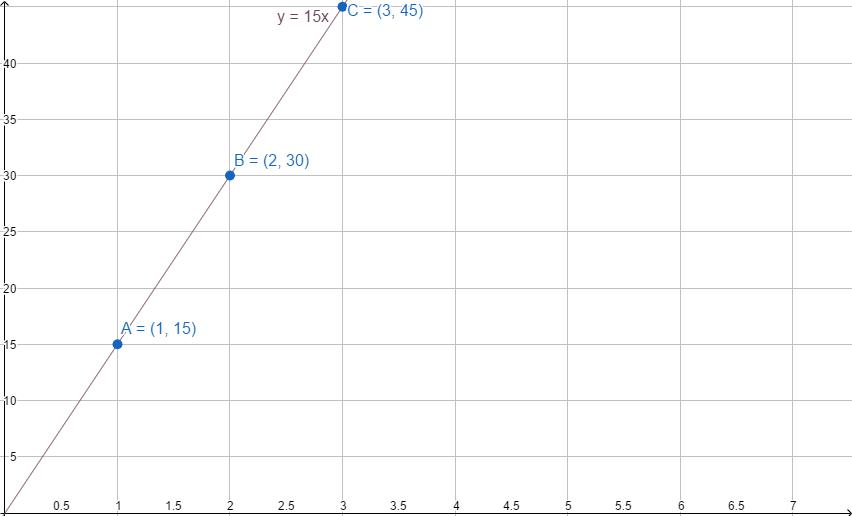
Vzdálenost, kterou osoba cestuje na kole, se bude lišit lineárně v závislosti na počtu hodin, které cestuje. Pokud jede 15 kilometrů za hodinu (bod A), za dvě hodiny bude řídit 30 kilometrů (bod B), za tři hodiny - 45 (bod C).
Závislost je popsána rovnicí y = 15x. Jak načrtnout lineární funkci v tomto případě?
- najít souřadnice bodů, které jsou řešením rovnice;
- stavěte je na rovině souřadnic;
- propojte tyto body s čárou.
Popis algoritmu
Hledání souřadnic bodů, které jsou řešením rovnice, snižuje nalezení dvou bodů, které jednoznačně definují čáru. Ačkoli stačí zvolit dvě různé hodnoty x a najít odpovídající hodnoty y, lze najít tři páry hodnot pro samokontrolování. To vám umožní rychle zjistit případnou chybu ve výpočtech. Často je první hodnota x zvolena jako nula.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| y = 0 | y = 15 |
Druhá hodnota x pro velké k je lepší vybrat vedle prvního. V opačném případě bude existovat silná rozptyl v hodnotách y a x, například u x = 4 v uvažované rovnici, y = 60. V každém případě před vykreslením lineární funkce v nalezených bodech je zvolena stupnice.
| y = 25 x | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 × 1 | |
| y = 0 | y = 25 |
Koeficient pro x
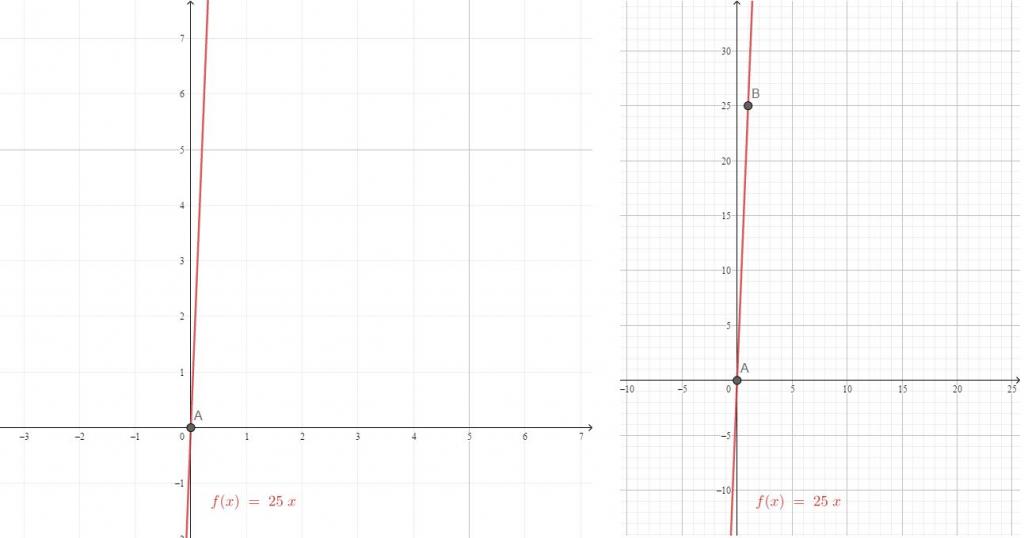
Rovnice lineární funkce má tvar y = kx + b. V závislosti na změně koeficientu pro neznámé se změní i charakter grafu lineární funkce y = kx.
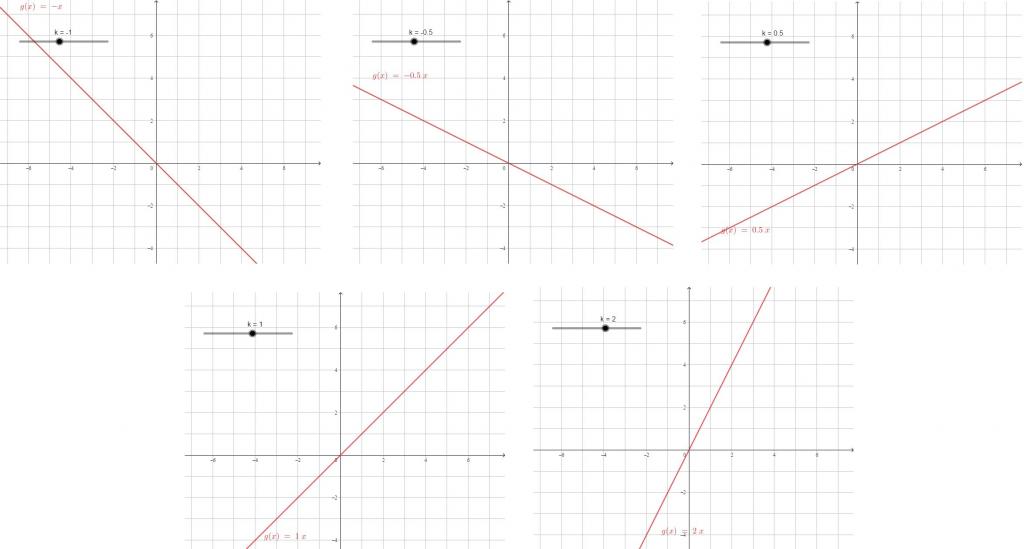
Čím větší je koeficient modulu, tím větší je strmost přímky, tím silnější pro stejnou změnu v hodnotách x se hodnoty y mění. Koeficient x je koeficient proporcionality.
Poměr zdarma
Volný koeficient je konstanta, která nezávisí na změnách hodnoty x. Ukazuje, kde linka protíná OY.
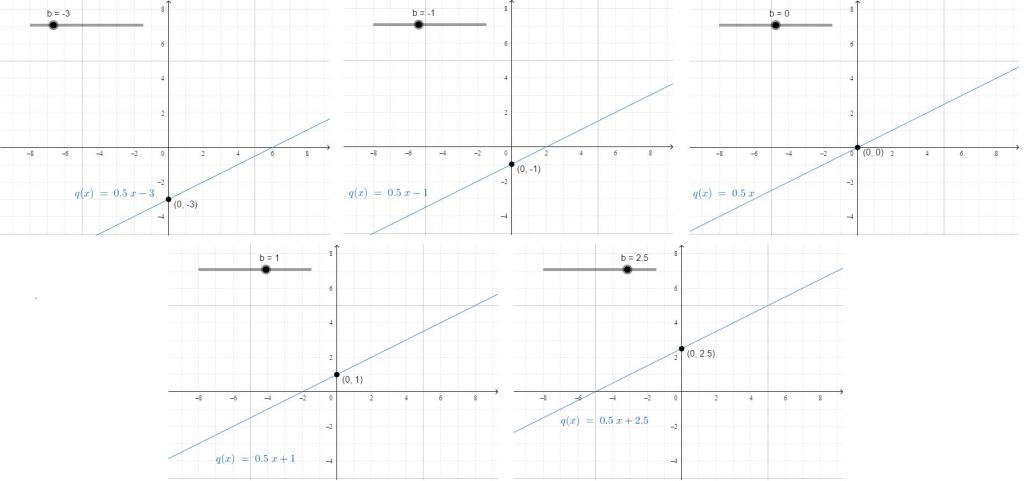
Například člověk šel 10 kilometrů od rána do 12 hodin odpoledne a pak jezdil na kole po dobu tří hodin. Dále vzdálenost, kterou pokrýval za den: y = 15 × 3 + 10. Pokud chcete odvodit vzorec pro výpočet vzdálenosti na konci každé hodiny od tří, které jízdil na kole, můžete použít: y = 15x + 10. V jednu hodinu den jel 15 × 1 a dalších 10 prošel, ve dvě hodiny jel 15 × 2, ale prošel kolem 10.
Graf lineární funkce y = kx + b popisuje čáru, která má sklon k a protíná OY v bodě se souřadnicemi (0, b). Analýza rovnice vám často umožňuje vyřešit problémy bez vytváření grafu. Aby však bylo možné pracovat v mysli, musí být akce opatřeny vizuálním materiálem.
Například úkolem je najít průsečíky y = - x 2 a y = 0.5x + 5. První funkce je klesající, druhá se zvyšuje, první je pod druhou, protože větve paraboly jsou dolů a její vrchol je původem. Lineární funkce by měla mít mnohem větší úhel sklonu, aby byla strmější a překročila jednu z větví paraboly. Proto je možné jednoznačně určit, že neexistují průsečíky bez konstrukce grafu a bez náhrady.
Zvláštní případy
- Pokud neexistuje žádný volný koeficient, je (ve skutečnosti) rovný nule, což znamená, že přímka protíná OY na nulu.
- Pokud neexistuje neznámý x nebo y, y a x jsou navzájem nezávislé. Například y = 5. Nezáleží na tom, jakou hodnotu má x, y bude vždy 5. Graficky to může být reprezentováno jako přímka rovnoběžná s OX.
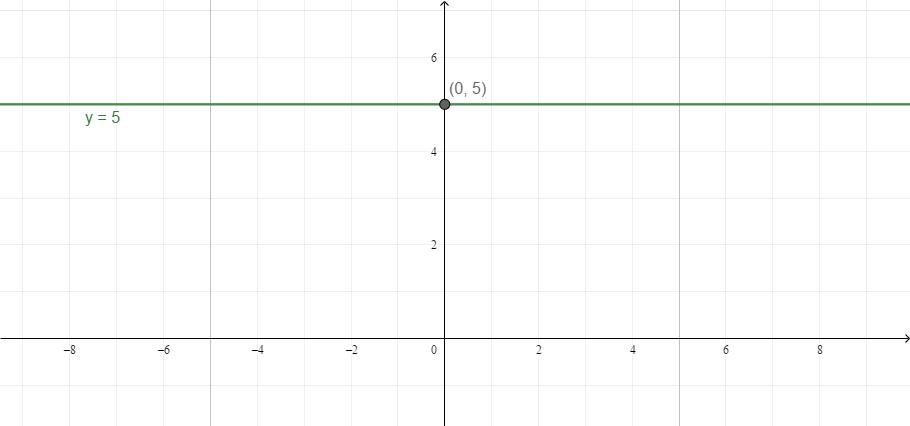
- Totéž platí pro případ, kdy se proměnná x rovná číslu: proměnná x má konstantní hodnotu.
Analýzou rovnice před vykreslením lineární funkce můžete zjistit její přibližnou polohu na OY a úhlu sklonu a tedy i sklonu. To pomáhá nejen najít správnou stupnici a sestavit graf, ale také řešit některé problémy v mysli.