Jak najít prémiové čísla?

Čísla jsou různá: přirozená, přirozená, racionální, celočíselná a částečná, pozitivní a negativní, složitá a jednoduchá, lichá a rovná, reálná atd. Z tohoto článku se můžete dozvědět, jaké jsou jednoduché čísla.

Jaké čísla se nazývají anglické slovo "simpl"?

Velmi často studenti na jedné z nejkomplikovanějších na první pohled otázky matematiky, o tom, co je primární číslo, nevědí, jak odpovědět. Často zaměňují jednoduchá čísla s přirozenými čísly (tj. Čísla, která lidé používají při počítání položek, zatímco v některých zdrojích začínají od nuly a v jiných - od jednoho). Ale to jsou zcela dvě odlišné věci. Prime čísla jsou přirozená, tj. Celá čísla a kladná čísla, která jsou větší než jedna a mají pouze 2 přirozené děliče. V tomto případě je jedním z těchto dělitelů dané číslo a druhý je jeden. Například tři jsou prvočíselné číslo, jelikož to není dělitelné jiným číslem než samým a jedním.

Čísla sloučenin

Opačný vzorec je složen. Jsou také přirozené, také více než jeden, ale nemají dvě, ale větší počet dělitelů. Čísla 4, 6, 8, 9 atd. Jsou například přirozená, kompozitní, ale ne primární čísla. Jak vidíte, jsou to převážně sudé čísla, ale ne všechny. Ale "dva" - sudé číslo a "první číslo" v řadě prvočísel.

Sekvence

Chcete-li sestavit řadu prvočísel, je nutné provést výběr ze všech přirozených čísel, přičemž je třeba vzít v úvahu jejich definici, to znamená, že musíte jednat opakem. Je nutné zvážit každé z kladných celých čísel, zda má více než dva děliče. Pokusíme se vytvořit řadu (sekvence), která tvoří hlavní čísla. Seznam začíná dvěma, druhý je tři, protože je rozdělen pouze na sebe a do jednotek. Zvažte číslo čtyři. Má děliče kromě čtyř a jednoho? Ano, toto číslo je 2. Takže čtyři nejsou primární číslo. Pět je také jednoduché (není dělitelné jiným číslem kromě 1 a 5), ​​ale šest je dělitelné. A obecně, pokud budete sledovat všechna sudá čísla, můžete vidět, že kromě "dvou", žádný z nich není jednoduchý. Z toho vyplývá, že dokonce i čísla kromě dvou nejsou jednoduchá. Další objev: všechna čísla dělitelná do tří, s výjimkou samotné trojice, ať už je lichá nebo lichá, nejsou také jednoduché (6, 9, 12, 15, 18, 21, 24, 27 atd.). Totéž platí pro čísla, která jsou rozdělena na pět a sedm. Všechny z nich také nejsou jednoduché. Shrňme. Takže jediné číslice jsou všechny lichá čísla s výjimkou jednoho a devíti a od sudé - pouze "dvě". Samotné desítky (10, 20, ... 40 atd.) Nejsou jednoduché. Dvouciferné, tříčlenné a další jednoduché číslice lze stanovit na základě výše uvedených zásad: pokud nemají jiné dělitele než ty a ostatní.

Teorie o vlastnostech prvočísel

Existuje věda, která studuje vlastnosti celých čísel, včetně prvků. Toto je odvětví matematiky, které se nazývá nejvyšší. Kromě vlastností celých čísel se také zabývá algebraickými, transcendentálními čísly, stejně jako funkcemi různých původů spojených s aritmetikou těchto čísel. V těchto studiích se kromě elementárních a algebraických metod používají také analytické a geometrické metody. Konkrétně studie primárních čísel zapojených do teorie čísel.

Prvotní čísla jsou "stavebními kameny" přirozených čísel.

V aritmetice existuje věta, která se nazývá hlavní teorém. Podle něho může být libovolné přirozené číslo kromě jednoho reprezentováno jako produkt, jehož faktory jsou jednoduché a sekvenční pořadí faktorů je jedinečné, což znamená, že způsob reprezentace je jedinečný. To se nazývá rozklad přirozeného čísla na primární faktory. Pro tento proces existuje jiný název - faktorizace čísel. Vycházíme z toho, že jednoduchá čísla se nazývají "stavební materiál", "bloky" pro konstrukci přirozených čísel.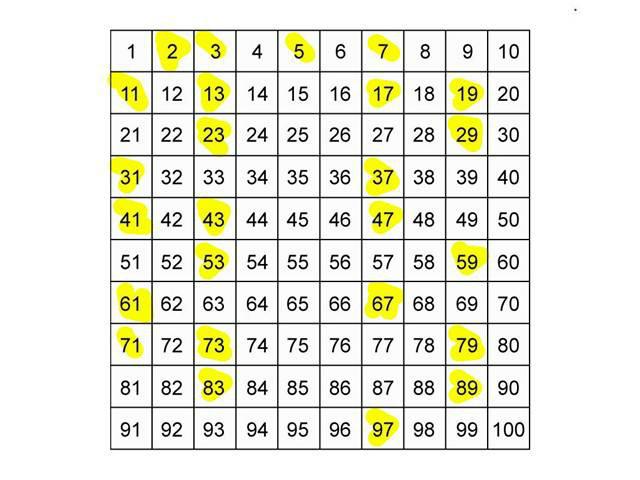

Vyhledejte počáteční čísla. Zkoušky jednoduchosti

Mnoho vědců různých časů se pokusilo najít nějaké principy (systémy) pro nalezení seznamu prvočísel. Věda ví systémy, které se nazývají síto Atkin, sítko Sundartam a síto Eratosthenes. Neposkytují však žádné významné výsledky a jednoduchá kontrola se používá k nalezení primárních prvků. Také matematici vytvořili algoritmy. Jsou nazývány testy jednoduchosti. Například je test vyvinutý Rabinem a Millerem. Používají ho kryptografové. K dispozici je také test Kayal-Agraval-Sasken. Přes jeho dostatečnou přesnost je však velmi obtížné vypočítat, což snižuje jeho praktickou hodnotu.

Má soubor prvotních čísel limit?

Skutečnost, že soubor jednoduchých je nekonečno, napsal v knize "Principy" starověký řecký učenec Euclid. Řekl to takto: "Představme si na okamžik, že primes mají limit. Pak je rozdělíme a přidáme do produktu jeden. Číslo získané v důsledku těchto jednoduchých akcí nemůže být rozděleno do jednoho z počtu prvočísel, protože ve zbytku bude vždy jedno. A to znamená, že je v seznamu prvních čísel ještě nějaké jiné číslo. Proto náš předpoklad není pravdivý a tento soubor nemůže mít limit. Kromě důkazu o Euclidu je modernější vzorec, který dal švýcarský matematik Leonard Euler z osmnáctého století. Podle něj součet inversní k součtu prvních n čísel roste bez omezení, protože počet n roste. Ale vzorec věty o distribuci prvočísel: (n) roste jako n / ln (n).

Jaké je největší číslo?

Totéž Leonard Euler dokázal najít jeho největší šanci. To je 2 ³¹ - 1 = 2147483647. Nicméně, do roku 2013, byl vypočítán druhý nejpřesnější jeden v seznamu prvních čísel, 2 ^57885161-1 , nazývá se Mersenne číslo. Obsahuje asi 17 milionů desetinných míst. Jak vidíte, počet nalezený vědci z osmnáctého století je několikrát menší než toto. Muselo to být tak, protože Euler robil tento výpočet ručně, ale náš počítač pravděpodobně pomohl náš současník. Navíc bylo toto číslo získáno na fakultě matematiky na jedné z amerických fakult. Čísla pojmenovaná podle tohoto vědce procházejí testem Luke-Lemere. Věda se však nechce zastavit. Nadace Electronic Frontier, která byla založena v roce 1990 ve Spojených státech amerických (EFF), jmenovala finanční odměnu za nalezení velkých prvočísel. A pokud se do roku 2013 na tuto cenu spoléhají ti vědci, kteří by je našli z deseti a desíti milionů desetinných čísel, dnes tato hodnota dosáhla 100 milionů až 1 miliardy. Velikost cen se pohybuje od 150 do 250 tisíc amerických dolarů.

Názvy speciálních prvků

Ty čísla, která byla nalezena díky algoritmům vytvořeným jedním nebo druhým vědcem a prošla zkouškou jednoduchosti, se nazývají zvláštní. Zde jsou některé z nich:

1. Merssen.

2. Wooda.

3. Farma.

4. Cullen.

5. Prota.

6. Mills a kol.

Jednoduchost těchto čísel, pojmenovaná podle výše uvedených vědců, je stanovena pomocí následujících testů:

1. Luc-Lemer.

2. Pepin.

3. Rizel.

4. Billhart - Lemera - Selfridge atd.

Moderní věda tam nekončí a je pravděpodobné, že v blízké budoucnosti bude svět znát jména těch, kteří by mohli získat cenu 250 000 dolarů a najdou největší počáteční číslo.