Jak najít střední řádek trojúhelníku? Základní vlastnosti, definice a metody
Někdy témata, která jsou vysvětlena ve škole, nemusí být vždy jasná od prvního okamžiku. To platí zejména o takovém předmětu jako je matematika. Ale vše se stává mnohem komplikovanější, když se tato věda začne rozdělovat na dvě části: algebra a geometrie.
Každý student má schopnost jednat ze dvou směrů, ale především v základních třídách je důležité pochopit základy algebry i geometrie. V geometrii je jednou z hlavních témat řez o trojúhelnících.
Jak najít střední řádek trojúhelníku? Zjistíme to.
Základní pojmy
Za prvé, abychom zjistili, jak najít střední řádek trojúhelníku, je důležité pochopit, co to je.
Neexistují žádné omezení pro držení středové čáry: trojúhelník může být libovolný (rovnoramenný, rovnostranný, obdélníkový). A všechny vlastnosti, které patří do středové čáry, budou jednat.
Středová čára trojúhelníku je segment spojující středy obou stran. Proto každý trojúhelník může mít 3 takové řádky.
Vlastnosti
Abychom věděli, jak najít střední řádek trojúhelníku, pojmenujte jeho vlastnosti, které je třeba si uvědomit, jinak bez nich nebude možné vyřešit problémy s nutností určit délku středové čáry, protože všechny získané údaje musí být doloženy a argumentovány věty, axiomy nebo vlastnostmi.
Ad
- Středová čára je rovnoběžná s bokem tohoto geometrického tvaru a je rovna 1/2. To naznačuje, že pokud se například strana rovná 8, pak se střední čára rovná 4.
- Provedeme v daném geometrickém obrázku všechny možné průměrné čáry, obdržíme 4 trojúhelníky, stejné a podobné. Rovněž jejich koeficient podobnosti se rovná 1/2.
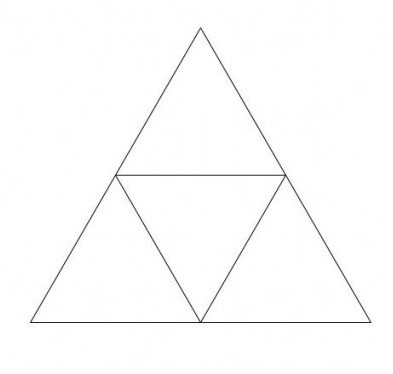
- A poslední vlastnost, že jedna nakreslená střední čára rozděluje hlavní trojúhelník na lichoběžník a trojúhelník.
Tak, abychom odpověděli na otázku: "Jak najít střední řádek ABC trojúhelníku?" Stačí, abyste poznali jednu ze stran trojúhelníku.
Uveďte příklad
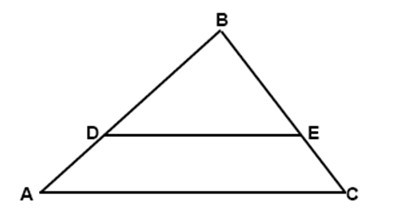
Podívejte se na obrázek. Představuje trojúhelník ABC se střední čárou DE. Všimněte si, že je rovnoběžný se základnou AC v trojúhelníku. Proto bez ohledu na hodnotu AC bude střední řada DE dvakrát menší. Například AC = 20, pak DE = 10 atd.
Zde můžete pochopit tak jednoduchými způsoby, jak najít střední řádek trojúhelníku. Nezapomeňte na jeho základní vlastnosti a definici a nikdy nebudete mít problémy najít jeho hodnotu.