Jak vytvořit rovnici ve dvou bodech: dvourozměrné a trojrozměrné případy
Přímka v geometrii je jedním z nejdůležitějších prvků, jelikož se od ní shromažďuje mnoho postav, a to jak v rovině, tak ve vesmíru. Stačí jmenovat trojúhelník, rovnoběžník, hranol, pyramidu - všechny jsou tvořeny protínajícími přímkami. Tento článek zodpoví otázku, jak vytvořit přímku rovnici pomocí dvou bodů.
Rovnice řádku pro dvourozměrné a trojrozměrné případy
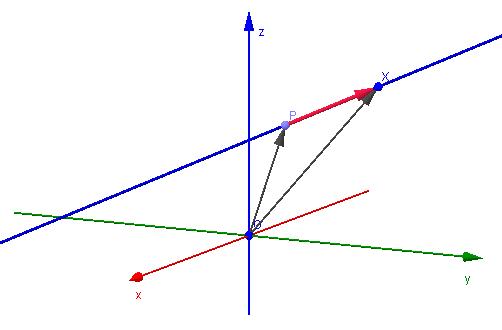
Než začnete diskutovat o tom, jak sestavit rovnici z dvou bodů, měli byste pochopit, co je v sázce.
Rovnicí přímky se rozumí rovnost spojená s přijatým souřadnicovým systémem a všechny hodnoty proměnných, které ji uspokojují, musí ležet na jedné přímce. V dvourozměrných a trojrozměrných případech lze tuto rovnici definovat následovně:
Q = P + α * u
Zde Q je souřadnice libovolného bodu linky, P je souřadnice určitého bodu patřícího k linii, u je směrový vektor, α je libovolné reálné číslo. Směrový vektor u je rovnoběžný s přímkou. Tento výraz se nazývá rovnice parametrů a vektorů.
Ve dvourozměrném případě je každý bod v rovině jednoznačně definován dvěma souřadnicemi x a y, takže můžete psát rovnici řádku ve tvaru:
(x, y) = (x 0 ; y 0 ) + α * (a; b)
Kde (x 0 ; y 0 ) jsou souřadnice známého bodu čáry, (a; b) jsou souřadnice řídícího vektoru. V parametrické formě může být tato rovnice přepsána jako systém dvou rovnic:
x = x 0 + α * a;
y = y 0 + α * b.
Vyjádřením parametru alfa a rovnocennosti získaných rovností se dostaneme do podoby:
y = b / a * x + (y 0- x 0 * b / a) nebo
y = A * x + C, kde A = b / a, C = (y 0 - x 0 * b / a)
Výsledný výraz je pro každého studenta obeznámen. Nazývá se obecná rovnice čáry v rovině.
Ve vesmíru je každý bod dán nikoliv dvěma, ale třemi souřadnicemi, proto jeho parametricko-vektorová rovnice má podobu:
(x, y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Parametr-vektorová rovnice je vhodná pro použití, když potřebujete vytvořit rovnici přímky procházející dvěma body.
Přímka a dva body
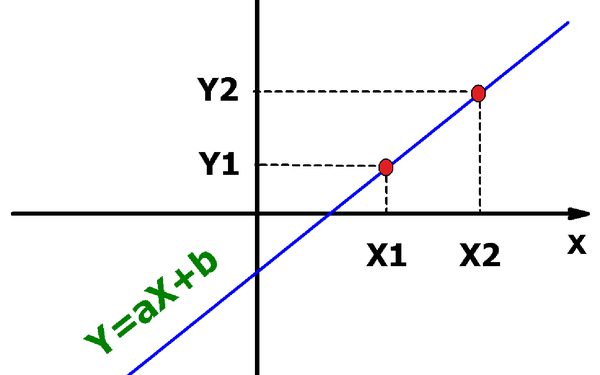
Nyní zvážíte problém článku přímo. Jak vytvořit přímou rovnici pomocí dvou bodů? Nejprve získáme rovnici v rovině a pak ji zobecňujeme pro trojrozměrný případ.
Předpokládejme, že na rovině P (x 1 ; y 1 ) a Q (x 2 ; y 2 ) jsou dva body. Pokud použijeme rozdíl mezi souřadnicemi bodů, pak získáme vektor, který je směrován z jednoho z nich do druhého. Tento vektor se rovná:
PQ¯ (x 2- x 1 ; y 2- y 1 )
V tomto případě je PQ¯ směrován z P (začátek řízeného segmentu) na Q (jeho konec). Vzhledem k tomu, že oba body patří k linii, patří k němu vektor PQ. To znamená, že může být považováno za vedení. Rovnice přímky má podobu:
(x, y) = (x 1 , y 1 ) + α * (x 2- x 1 ; y 2- y 1 )
Zde jsme vzali bod P. Pokud jej nahradíme bodem Q, pak se rovnice nezmění.
Jak vytvořit rovnici přímky ve vesmíru pomocí dvou bodů? Shrnutí výsledné rovnice pro letadlo získáme:
(x, y; z) = (x 1 ; y 1 ; z 1 ) + β * (x 2- x 1 ; y 2 -y 1 ; z 2 -z 1 )
Druhé písmeno parametru je převedeno tak, aby ukázalo nezávislost této a předchozích rovnic.
Příklad řešení problému
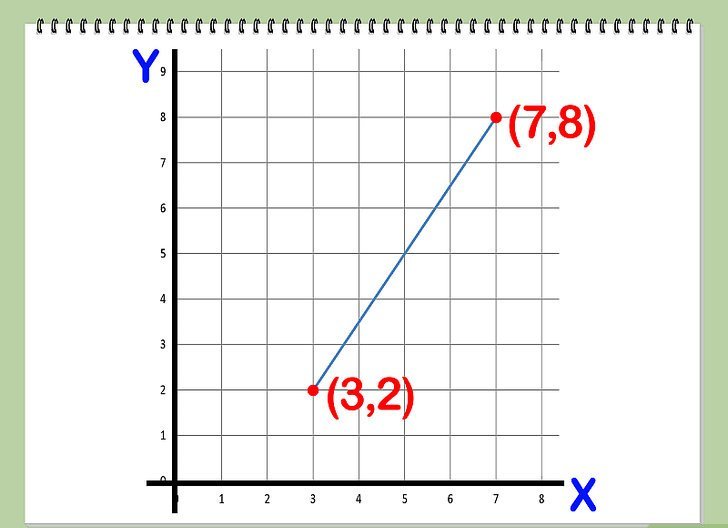
Když jsme zjistili, jak vytvořit přímou rovnici pro dva body, dáme příklad využití znalostí získaných pro dvourozměrný případ.
Předpokládejme, že v rovině (3; -4) a (0; 7) jsou body. Je nezbytné vytvořit přímou rovnici přes dva body.
Vypočítat souřadnice vodícího vektoru:
(0-3; 7 - (- 4)) = (-3; 11)
Parametr-vektorová rovnice má tvar:
(x; y) = (3; -4) + α * (- 3; 11)
Otevřete ji a přeneste ji do obecné podoby:
x = 3 - 3 * α => α = (x-3) / (- 3);
y = -4 + 11 * α => α = (y + 4) / 11;
(x-3) / (- 3) = (y + 4) / 11 =>
y = -11 / 3 * x + 7.
Máme rovnici v obvyklé (obecné) formě. Jeho platnost můžete ověřit nahrazením souřadnic obou bodů od stavu problému.