Interpolace je ... Definice, vlastnosti výpočtu a příklady interpolace

Mnoho z nás se setkalo s nepochopitelnými pojmy v různých vědách. Ale existuje jen velmi málo lidí, kteří se nebojí nepochopitelných slov, ale naopak nás povzbuzují a nutí, abychom se stále více zabývali předmětem, který je studován. Dnes budeme mluvit o takové věci jako interpolace. Jedná se o způsob vytváření grafů ze známých bodů, který umožňuje s minimálním množstvím informací o funkci předpovědět jeho chování na konkrétních částech křivky.

Než se obrátíme na podstatu samotné definice a podrobněji o ní řekneme, ponoříme se trochu do příběhu.

Dějiny

Interpolace je známá od dávných dob. Tento jev však vděčí vývoji několika nejvýznamnějším matematikům minulosti: Newtonovi, Leibnizovi a Gregorymu. Vyvinuli tento koncept pomocí pokročilejších matematických metod, které byly v té době k dispozici. Předtím byla interpolace samozřejmě použita a použita ve výpočtech, ale byla provedena zcela nepřesnými způsoby, které vyžadují velké množství dat, aby se vytvořil model, který je více či méně blízký realitě.

Dnes můžeme dokonce zvolit, která metoda interpolace je vhodnější. Všechno bylo přeloženo do počítačového jazyka, který s velkou přesností dokáže předpovědět chování funkce v určité oblasti, ohraničené známými body.

Interpolace je spíše úzká koncepce, proto její historie není tak bohatá na fakta. V další části pochopíme, jaká je interpolace a jak se liší od její opačné - extrapolace.

Co je to interpolace?

Jak jsme již řekli, je to obecný název způsobů, jak vytvořit graf podle bodů. Ve škole se to dělá hlavně sestavením tabulky, určením bodů na grafu a zhruba vytvořením spojů, které je spojují. Poslední akce je provedena na základě úvah o podobnosti zkoumané funkce ostatním, typu grafů, které známe.

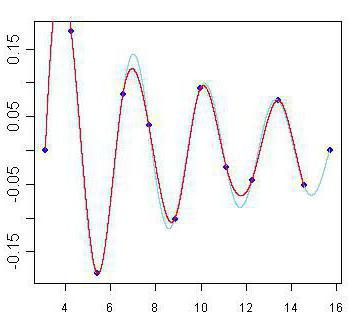
Existují však jiné, složitější a přesnější způsoby, jak splnit úkol vykreslování bodů. Takže interpolace je vlastně "předpověď" chování funkce v určité oblasti, ohraničené známými body.

Existuje podobná koncepce spojená se stejnou oblastí - extrapolací. Představuje také předpověď grafu funkce, ale za známé body grafu. Pomocí této metody je předpověď provedena na základě chování funkce na známém intervalu a pak se tato funkce aplikuje také na neznámé intervaly. Tato metoda je velmi praktická pro praktické použití a aktivně se používá například v ekonomice, aby předpovědi výkyvů a poklesů na trhu a předpovídala demografickou situaci v zemi.

Ale odklonili jsme se od hlavního tématu. V další části zjistíme, jaká interpolace se děje a s jakou formulací můžete tuto operaci provést.

Typy interpolace

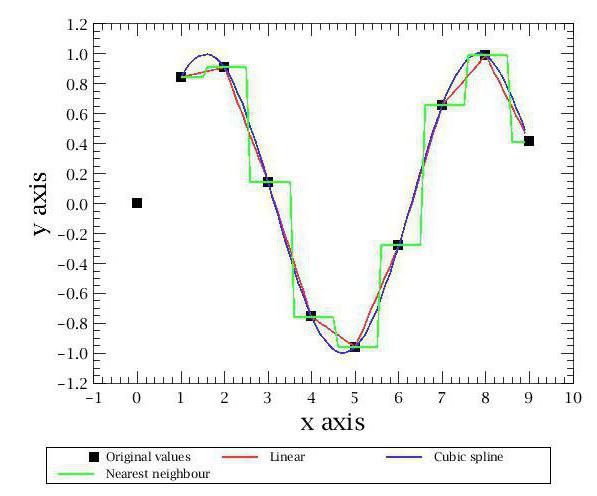
Nejjednodušší typ je nejbližší sousední interpolace. Tímto způsobem získáme velmi přibližný graf skládající se z obdélníků. Pokud jste alespoň jednou viděli vysvětlení geometrického významu integrálu na grafu, pochopíte, jakou grafickou podobu mluvíme.

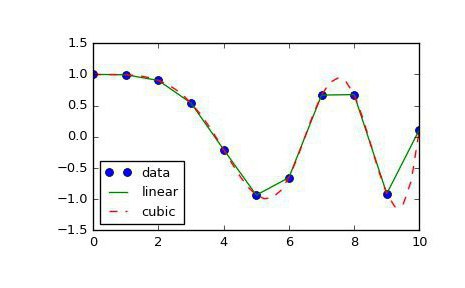
Kromě toho existují i ​​jiné metody interpolace. Nejznámější a nejoblíbenější jsou spojené s polynomy. Jsou přesnější a umožňují předpovídat chování funkce s poměrně nízkou hodnotou. První interpolační metoda, kterou považujeme za lineární interpolaci polynomy. To je nejjednodušší cesta z této kategorie a jistě každý z vás ji použil ve škole. Jeho podstatou spočívá v konstrukci přímých linek mezi známými body. Jak je známo, přímá přímka prochází dvěma body roviny, jejíž rovnice lze nalézt na základě souřadnic těchto bodů. Vytvářením těchto přímých linek získáváme zlomený graf, který je nějakým způsobem, ale odráží přibližné hodnoty funkcí a obecně se shoduje s realitou. Takto se provádí lineární interpolace.

Komplikované typy interpolace

Existuje zajímavější, ale složitější metoda interpolace. Vymyslel ho francouzský matematik Joseph Louis Lagrange. Proto je pojmenován výpočet interpolace pomocí této metody: Lagrangeova interpolace. Zaměření je zde: pokud metoda popsaná v předchozím odstavci používá pro výpočet pouze lineární funkci, pak Lagrangeův rozklad také zahrnuje použití polynomů vyšších stupňů. Ale není snadné najít interpolační vzorce pro různé funkce. A čím více bodů je známo, tím přesnější je interpolační vzorec. Existuje však spousta dalších metod.

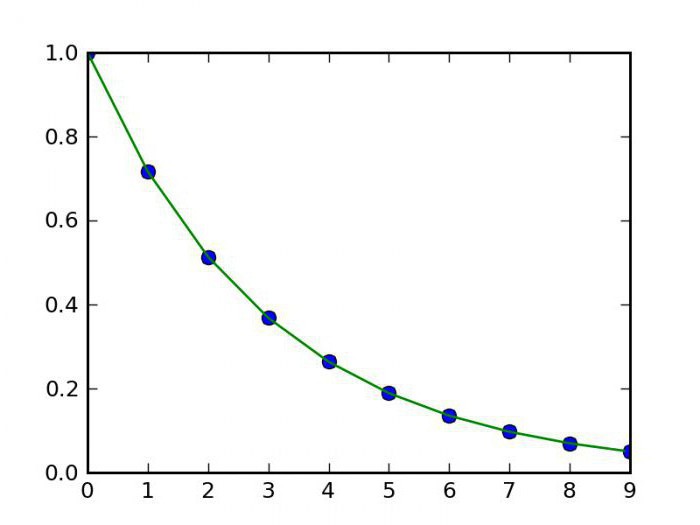
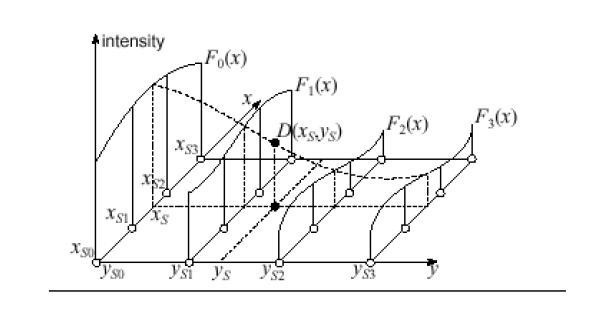
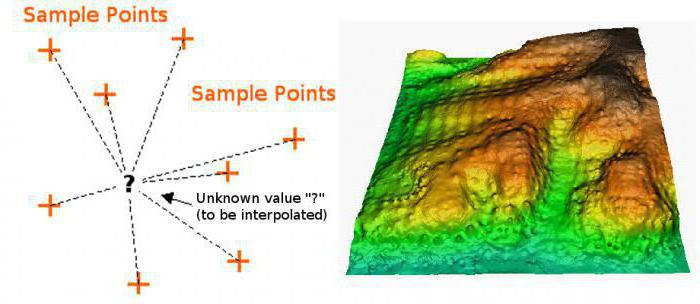
Existuje také dokonalá a realistická metoda výpočtu. Interpolační vzorec, který se v něm používá, je množina polynomů, jejichž použití závisí na oblasti funkcí. Tato metoda se nazývá funkce spline. Kromě toho existují také způsoby, jak provádět takovou věc jako interpolační funkce dvou proměnných. Existují pouze dvě metody. Mezi nimi bilineární nebo dvojitá interpolace. Tato metoda umožňuje snadno vytvořit graf podle bodů trojrozměrný prostor. Jiné metody neovlivní. Obecně platí, že interpolace je univerzální název pro všechny tyto metody grafování, ale různé způsoby, jak lze tuto akci provést, nutí je rozdělit do skupin v závislosti na typu funkce, která je předmětem této akce. To znamená, že interpolace, příklad, o kterém jsme se shledali výše, odkazuje na přímé metody. Existuje také inverzní interpolace, která se liší v tom, že nám umožňuje vypočítat ne přímou, ale inverzní funkci (to znamená x z y). Nebudeme zvažovat nejnovější možnosti, neboť je poměrně obtížné a vyžaduje dobrou znalost matematické základny.

Obracíme se na jednu z nejdůležitějších částí. Z toho se dozvídáme, jak a kde se soubor metod, o kterých diskutujeme, aplikuje v životě.

Aplikace

Matematika je známá jako královna věd. Proto i v případě, že nejste poprvé vidět bod v určitých operacích, to neznamená, že jsou zbytečné. Například se zdá, že interpolace je zbytečná věc, díky níž mohou být stavěny pouze grafy, které nyní potřebují jen málo lidí. Pro výpočty ve strojírenství, fyzice a mnoha dalších vědách (například v biologii) je mimořádně důležité poskytnout poměrně úplný obraz tohoto fenoménu a mít určitý soubor hodnot. Hodnoty rozmístěné podél grafu ne vždy poskytují jasnou představu o chování funkce v určité oblasti, hodnoty jejích derivátů a průsečíky s osami. A to je velmi důležité pro mnohé oblasti našeho života s vámi.

A jak je to užitečné v životě?

Na tuto otázku je velmi obtížné odpovědět. Ale odpověď je jednoduchá: žádný způsob. Tyto znalosti vám nebudou užitečné. Ale pokud rozumíte tomuto materiálu a způsobům, kterými se tyto akce provádějí, budete praktikovat svou logiku, která je v životě velmi užitečná. Hlavní věc není samotné poznání, ale dovednosti, které člověk získá v procesu učení. Koneckonců není divu, že se říká: "Žijte se a učíte se."

Související pojmy

Můžete pochopit sami sebe, jak důležitá (a přesto neztratí svou důležitost) tuto oblast matematiky, když se podíváte na rozmanitost dalších pojetí souvisejících s tímto. Již jsme hovořili o extrapolaci, ale existuje také přiblížení. Možná jste už slyšeli toto slovo. V každém případě to, co to znamená, jsme také diskutovali v tomto článku. Přibližování, stejně jako interpolace, je koncept spojený s konstrukcí grafů funkcí. Rozdíl mezi první a druhou je, že představuje přibližnou konstrukci grafu založeného na podobných známých grafech. Tyto dvě pojmy jsou velmi podobné a je zajímavější studovat každý z nich.

Závěr

Matematika není tak složitá věda, jak se zdá na první pohled. Je to docela zajímavé. A v tomto článku jsme se o to pokusili. Přezkoumali jsme pojmy spojené s konstrukcí grafů, zjistilame, jaká dvojitá interpolace je a rozebírá se s příklady, kde se používá.