Ostrogradsky - Gaussova věta a vzorec

Mv Ostrogradsky - ruský matematik a fyzik od ruské říše, akademik. Na rozvoj se významně podílel matematická analýza teorie pravděpodobnosti, mechanika (úsek fyziky) teorie čísel. V roce 1826 získal vzorec, který se nyní nazývá Ostrogradsky-Gaussův vzorec.

Historie objevů

Ostrogradský-Gaussův vzorec byl nejprve zmínil Joseph Lagrange v roce 1762.

Dále byl hlavní metodou redukce trojitého integrálu na povrch dokázán Karl Gauss, který jako základ důkazu použil řešení problémů v elektrodynamice. Stalo se to v první polovině 19. století.

Dále vzorec v obecné podobě představil Michail Ostrogradský. S jeho pomocí bylo možné vyjádřit hodnotu diferenciálu v parametru z N-krát integrálu.

Význam vzorce Ostrogradsky

Ostrogradský-Gaussův vzorec spojuje trojitý integrál s prostorovým objemem s integrálem nad povrchem na jeho obličeji. Je to analogický vzorec Zelená, který se vztahuje k dvojitému integrálu v rovině s křivočarým podél jeho hranic.

Odvození vzorce

Ostrogradský - Gaussův vzorec: závěr. Předpokládejme, že v doméně W je definována integrantová funkce R (x, y, z), která je definovaná a spojitá. Jeho derivát je podobný v celé doméně W, včetně její hranice. V této podobě je nyní známa Věra Ostrogradského - Gaussova (vzorec je uveden níže).

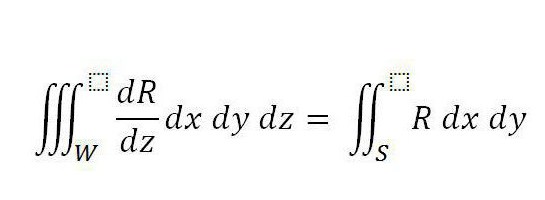
Navíc S je povrch, který ohraničuje tělo, a integrál vpravo je rozdělen na jeho vnější stranu.

A naprosto pravda

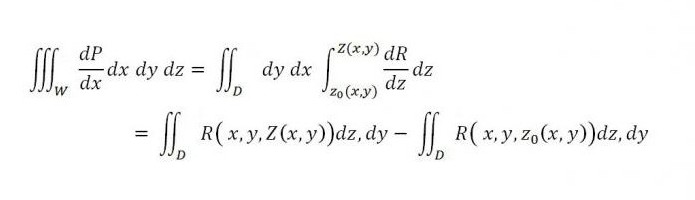
Pokud podobně přihlédneme k integrály nad povrchem, pak

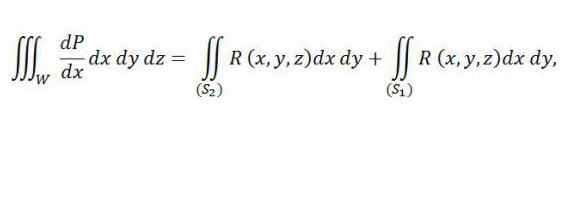
zatímco vpravo je součet dvou integrálů - první je vztažena k horní části plochy (S ₂ ) a druhé ke spodní části povrchu (S ₁ ). Pokud přidáme integrál uvedený níže do rovnosti vpravo, pak její platnost nebude porušena:

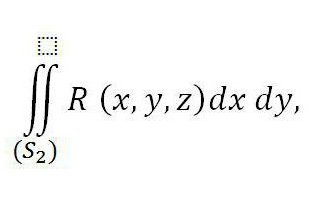
Odpovídá vnější části povrchu S _{3 v} důsledku rovnosti k nule.

Pokud spojíme všechny tři integrály do jednoho, získáme zvláštní případ Ostrogradského vzorce.

Je snadné si uvědomit, že tento vzorec platí pro širší třídu těles a je platný i pro obrázky ohraničené absolutně jakýmikoli nelineárními povrchy.

Rovněž platí následující vzorce:

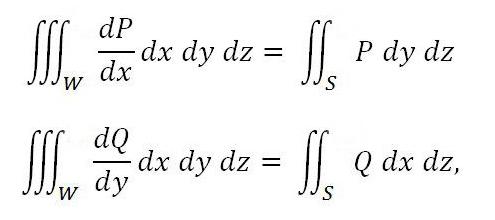
pokud jsou funkce Q a P kontinuální v doméně spolu s jejich deriváty dP / dx a dQ / dy.

Přidáme-li oba rovnosti, dostaneme výraz pro Ostrogradský vzorec. Zobrazuje integrál na povrchu, který je v korelaci s vnější částí povrchu, skrz trojitý integrál, který je převzat na samotné tělo, jehož hranicí je výše zmíněný povrch.

Mělo by být zřejmé, že vzorce Zelené, Stokesové a Ostrogradského vyjadřují integrál spojený s určitým geometrickým tělem prostřednictvím integrálu, který je zachycen na jeho hranici. Zelený vzorec je používán pouze v případě dvojrozměrnosti prostoru, Stokesův vzorec je aplikován na zakřivený dvourozměrný prostor.

Vzorec Newton-Leibniz může být také považován za nějaký analog tohoto vzorce, ale za jednorozměrný prostor.

Použití tohoto vzorce

Nechť kontinuální funkce A, B a C jsou uvedeny v libovolné neuzavřené oblasti prostoru. Vezmeme-li jakýkoli uzavřený povrch, který je v dané oblasti a ohraničuje určité tělo, můžeme zvážit následující integrál na povrchu:

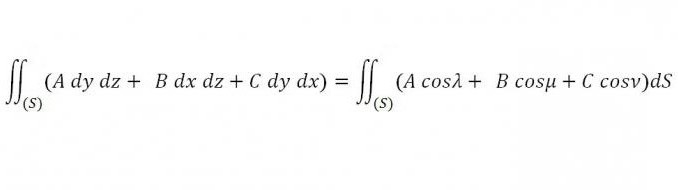
Je třeba najít takové hodnoty A, B a C tak, že pro všechny x, y a z tohoto integrálu se rovná nule.

K tomu použijte Ostrogradsky-Gaussův vzorec. Jednou z předpokládaných podmínek je jistota a kontinuita funkcí A, B a C a jejich derivátů.

Také je nutné specificky zavést nejdůležitější omezení pro daný případ: jak tělo, tak jeho ohraničení musí být obsaženo současně v určité a specifikované oblasti, nazývané jednoduše připojené. Jeho hlavním rysem je absence prázdného prostoru (včetně bodového prostoru). Tedy, hranice těla bude jedna a ten s jedním povrchem.

Po uplatnění vzorce je možné získat následující podmínku, která je dostatečná:

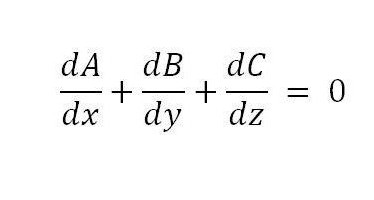
Abychom dokázali, že podmínka je také nezbytná, stačí použít diferenciaci trojitého integrálu.

Závěrem je třeba říci o oblastech použití.

Jak se v praxi používá Ostrogradsky-Gaussův vzorec? Příklady použití lze nalézt v různých oblastech: odvodit nějaké vzorce ve fyzice (například rovnice difúze), transformovat integrály, vypočítat Gaussovy integrály, prokázat některé vzorce a mnohem více.