Přehled různých typů hranolů. Vlastnosti trojúhelníkových hranolů

Prism je jednou z nejznámějších osobností ve vesmíru, jejichž vlastnosti jsou podrobně studovány v geometrickém kurzu školy. Tento článek je přehledem různých typů hranolů a jejich charakteristik. Charakteristiky trojúhelníkového hranolu jsou podrobněji popsány.

Co je hranol?

Začneme článek s definicí hranolu v geometrii. Pod touto postavou má být tvarován dvěma identickými rovnoběžnými stranami, které jsou plochými n-gony a n paralelogramovými stranami. Jakýkoliv tvar, který splňuje zaznamenanou definici, bude hranolem.

Vybudování hranolu pomocí geometrických operací není obtížné. Je nutné pouze vzít absolutně n-gon a přenést jej paralelně na sebe pro určitý segment ve vesmíru.

Vzhledem k tomu, že daným číslem je polyhedron (sestává z polygonálních ploch), nemůže být geometricky dosažen rotací, jak je to možné u válce nebo kužele.

Každý hranol má dvě základny, které jsou reprezentovány rovnými n-gony a n paralelogramy (někdy mohou být obdélníky, čtverce nebo kosočtverečky), jejichž celkový tvar tvoří boční povrch postavy. Rovněž je charakteristická 2 * n rovnými vrcholy a 3 * n hranami, kde n je počet stran (vrcholů) polygonální základny.

Jak jsou hranoly klasifikovány?

Počet různých hranolů je nekonečný. Všechny se navzájem liší ve tvaru a lineárních rozměrech, nicméně existují pouze dva znaky jejich geometrické struktury, které jsou základem moderní klasifikace dané třídy čísel. Tyto funkce jsou následující:

• základní typ polygonu;
• úhly mezi stranami a základnami.

Žádné další parametry než ty, které jsou uvedeny výše, ovlivňují vzhled hranolu. Obě funkce dohromady vedou k rozdělení celé třídy na čtyři typy nebo typy čísel:

• konvexní a konkávní;
• trojúhelníkový čtyřúhelník, ..., n-uhlík;
• rovný a šikmý;
• správně a špatně.

Podívejme se podrobněji na každý z těchto typů hranolů, jejichž vlastnosti jsou jednoznačně určeny výše uvedenou klasifikací.

Konvexní a konkávní postavy

Mnoho lidí zapomíná na tento klasifikační prvek, když charakterizuje hranoly, protože ve všech geometrických problémech se zpravidla objevují výrazné postavy. Vyzývá se tedy konvexní hranol, který má na základně konvexní mnohoúhelník. Proto pokud je polygon konkávní, hranol bude také konkávní.

Dále v článku budou ukázány pouze konvexní hranoly, ale zde ukážeme, jak vypadá konkávní deseúhelníkový hvězdicovitý hranol.

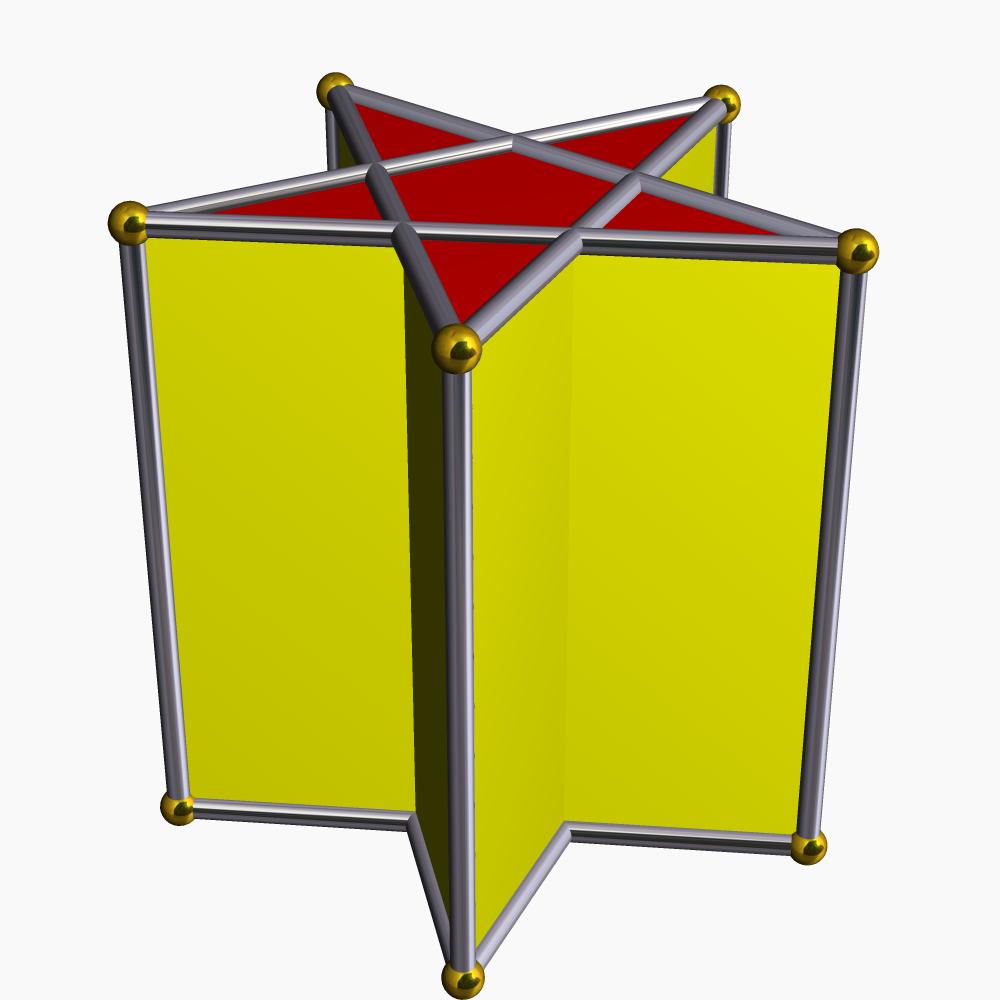
Všimněte si, že konkávní hranol s minimálním počtem stran na základně bude mít čtverhranný tvar, zatímco pro konvexní hranol je to trojúhelníkový tvar.

Polygonální hranoly

Možná je to nejznámější typ klasifikace položek hranolů. Trojúhelníkový, čtverhranný, pětiúhelníkový a tak dále budou hranoly nazývány postavy, které mají odpovídající základnu. Například obrázek ukazuje 6 různých hranolů - od trojúhelníkových po osmiúhelníky.

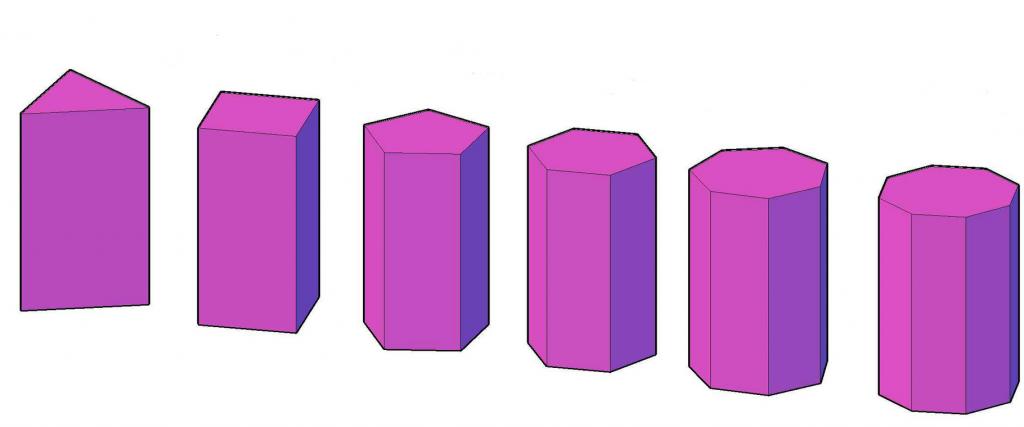
Mezi všemi typy polygonálních hranolů má jen čtyřúhelník své vlastní jméno - rovnoběžnost. Druhá, s určitými lineárními a úhlovými parametry, se může stát kostkou.

Šikmé a rovné postavy

Klasifikace šikmých a přímých hranolů je založena na dvojitých úhlech mezi stranami postavy a její základny. Pokud jsou všechny tyto dihedralské úhly rovny 90 ^° , pak se hranol nazývá rovný nebo obdélníkový. Pokud není alespoň jeden úhelník v pořádku, pak se tento údaj považuje za nakloněný nebo šikmý. Připomeňme si, že mluvíme pouze o dvojitých úhlech mezi základnou a stranami. Dvojité úhly mezi stranami nejsou brány v úvahu.

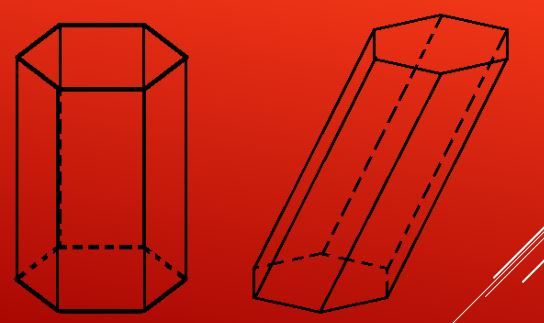
Výše uvedené ukazuje, jak vypadají šikmé a pravé šestiúhelníkové hranoly. Obrázek ukazuje, že strany hranolu jsou obdélníky (čtverce). Různé typy přímých hranolů a šikmých je možné získat změnou počtu stran polygonů v jejich podstavcích.

Správná a špatná čísla

Jednoduše řečeno, pokud je hranol rovný a jeho základ je správný n-gon, pak bude také správný. Všechny ostatní hranoly, které nesplňují popsané podmínky, jsou nesprávné.

Obrázek výše, který ukazuje šest polygonálních hranolů, ukazuje pravidelné tvary.

Je vhodné prozkoumat vlastnosti pravidelných hranolů, protože pro každý z nich existují specifické vzorce pro určení jejich výšky, plochy, objemu, úhlopříčky a dalších charakteristik.

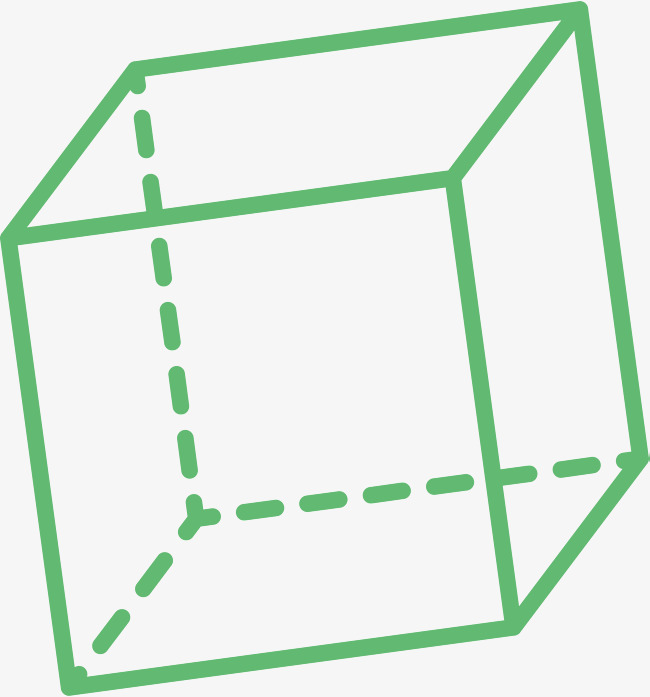
Pravý čtverhranný hranol, jehož výška je rovna straně jeho základny, se nazývá krychle.

Trojúhelníkové hranoly

Pojďme se zabývat trojúhelníkovými hranolky, protože jsou nejjednodušší mezi třídami uvažovaných čísel.

Každý takový tvar má 5 tváří, 6 stejných vrcholů a 9 okrajů. Objemy trojúhelníkových hranolů jsou vypočteny podle vzorce, které platí pro všechny hranoly. Vypadá to takto:

V = S _o * h.

Objem se rovná součinu plochy jedné základny a výšky obrázku. V případě pravidelného hranolu se stranou a trojúhelníku má tento vzorec podobu:

V = √3 / 4 * a ² * h.

Vzhledem k otázce typů hranolů je plocha trojúhelníkových hranolů definována jako součet ploch dvou identických trojúhelníků a tří paralelogramů. Je-li to správný hranol, platí následující vzorec pro plochu S:

S = √3 / 2 * a ² + 3 * a * h.

Při psaní tohoto výrazu jsme použili skutečnost, že ve správném hranolu jsou všechny strany rovny a jsou obdélníky.