Paradox Monty Hall. Nejpřesnější matematika

Teorie pravděpodobnosti je větev matematiky, která je připravena zaměnit samotné matematiky. Na rozdíl od ostatních, přesných a nepochopitelných dogmů této vědy, tato oblast je plná zvláštností a nepřesností. V této části byl nedávno přidán nový odstavec - paradox Monty Hall. Toto je obecně úloha, ale je řešena úplně jiným způsobem než školní nebo univerzitní, na které jsme zvyklí.

Historie původu

Přes paradox Monty Hall, lidé od roku 1975 rozbíjeli hlavu. Ale stojí za to počínat od roku 1963. To je, když se objevila televizní show s názvem Pojďme uzavřít dohodu, která se promítá jako "Pojďme se dohodnout." Jeho vedením nebyla nikdo jiný než Monty Hall, který hodil diváky někdy nepřekonatelné hádanky. Jeden z nejpozoruhodnějších byl ten, který představil v roce 1975. Úloha se stala součástí matematické teorie pravděpodobnosti a paradoxů, které se hodí do jejího rámce. Je také třeba poznamenat, že tento jev vedl k silným diskusím a tvrdým kritikám vědců. Paradox Monty Hall byl publikován v časopise Parade v roce 1990 a od té doby se stal ještě více diskutovanou a kontroverzní otázkou všech dob a národů. No, nyní postupujte přímo k jeho formulaci a interpretaci.

Formulace problému

Existuje mnoho interpretací tohoto paradoxu, ale rozhodli jsme se Vám představit klasiku, která se ukázala v samotném programu. Takže předtím, než jste tři dveře. Za jedním z nich je auto, za dvěma dalšími na jedné kozy. Facilitátor vás vyzývá, abyste si vybrali jednu z dveří, a řekněme, že zůstanete na čísle 1. Zatím nevíte, co je za těmito prvními dveřmi, protože otevřete třetí a ukažte, že za ní je koza. V důsledku toho jste ještě neztratili, protože jste nevybrali dveře, které skryjí možnost ztráty. V důsledku toho se vaše šance na získání auta zvýší.

Ale tady vám vůdce nabízí možnost změnit rozhodnutí. Než budete mít dvě dveře, za jednu kozu, za jinou požadovanou cenu. To je podstatou problému. Zdá se, že jakákoli ze dvou dveří, která si vyberete, jsou šance 50 až 50. Ale ve skutečnosti, pokud změníte rozhodnutí, pravděpodobnost, že vyhrajete, bude větší. Jak?

Vysvětlení paradoxu Monty Hall

První volba, kterou uděláte v této hře, je náhodná. Nemůžete ani odhadnout, která ze tří dveří je skrytá, takže náhodně ukazuje na první. Vedoucí, podle pořadí, ví, kde jsou věci. Má dveře s cenou, dveřmi, které jste uvedli, a třetí bez ceny, kterou vám otevírá jako první vodítko. Druhým náznakem je jeho návrh na změnu volby.

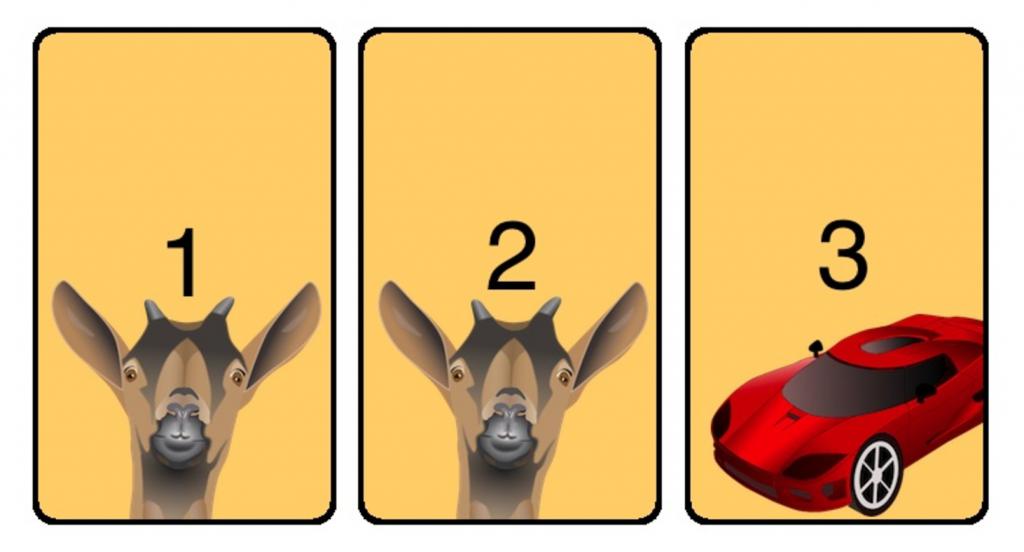
Teď si náhodně nevyberete jednu ze tří, ale můžete dokonce změnit své rozhodnutí získat požadovanou cenu. Je to vůdce, které dává člověku přesvědčení, že auto opravdu není za dveřmi, které si vybral, ale za druhým. To je celá podstata paradoxu, protože je třeba vybrat (nejméně ze dvou, a ne od tří) náhodně, ale šance na výhru. Jak ukazují statistiky, z 30 hráčů, kteří změnili názor, vyhrál auto 18. A to je 60%. A ze stejných 30 lidí, kteří rozhodnutí nezměnili - pouze 11, tedy 36%.

Léčba v číslech

Nyní poskytujeme paradoxu Monti Hall přesnější definici. První volba hráče přeruší dveře do dvou skupin. Pravděpodobnost, že se cena nachází za zvolenými dveřmi, je 1/3 a za dveřmi, které zůstávají 2/3. Facilitátor dále otevírá jednu z dveří druhé skupiny. Tím převede zbývající pravděpodobnost, 2/3, na jednu dveře, kterou jste si nevybrali a kterou neotevřel. Je logické, že po takových výpočtech bude výhodnější měnit vaše rozhodnutí. Je však důležité si uvědomit, že stále existuje možnost ztráty. Někdy vedoucí mazaný, jelikož se nejprve můžete pokoušet správné, dveře a poté dobrovolně odmítnout.

Všichni jsme zvyklí, že matematika, jako přesná věda, jde ruku v ruce se zdravým rozumem. Zde jsou to čísla, která to dělají, ne slova, přesná vzorce, ne vágní odrazy, souřadnice, ne relativní data. Ale jeho nová část nazvaná teorie pravděpodobnosti vybuchla celý známý vzor. Úkoly z této oblasti, zdá se nám, neinvestují do zdravého rozumu a zcela odporují všem formám a výpočtům. Navrhujeme níže seznámit se s dalšími paradoxy teorie pravděpodobnosti, které mají něco společného s tím, co bylo popsáno výše.

Paradox chlapce a dívky

Problém je na první pohled absurdní, ale striktně se řídí matematickým vzorem a má dvě možná řešení. Takže určitý muž má dvě děti. Jeden z nich je pravděpodobně chlapec. Jaká je pravděpodobnost, že chlapec bude druhý?

Možnost 1. Vezmeme v úvahu všechny kombinace dvou dětí v rodině:

• Dívka / dívka
• Dívka / chlapec
• Chlapec / dívka
• Chlapec / chlapec

První kombinace nám samozřejmě nevyhovuje, a proto na základě posledních tří, máme pravděpodobnost 1/3, že druhé dítě bude malý muž.

Možnost 2. Pokud si takový případ v praxi představíme a zbavíme se zlomků a vzorců, pak na základě skutečnosti, že na Zemi jsou pouze dvě pohlaví, pravděpodobnost, že druhé dítě bude chlapcem, je 1/2.

Paradox spící krásy

Tato zkušenost nám ukazuje, jak skvěle můžete manipulovat se statistikami. Takže spící krása je injektována spací pilulkou a mince je hodena. Pokud padne orlica, probudí se a experiment se zastaví. Pokud padnou ocasy, vzbudí ji, okamžitě provedou druhou injekci a zapomene, že se probudila, a pak se znovu probudí až druhý den. Po úplném probuzení k "kráse" není známo, kdy den otevřela oči, nebo jaká je pravděpodobnost, že mince padla jako ocas. Podle první varianty řešení je pravděpodobnost, že se ocas (nebo orel) dostane 1/2. Podstata druhé možnosti spočívá v tom, že když provedete experiment 1000krát, pak v případě orla se "krása" probuduje 500krát a se vzácným - 1000. Nyní je pravděpodobné, že ocasy jsou 2/3.