Parallax je to, co to je?

Cosmos je jedním z nejzákladnějších konceptů na světě. Když se podíváte na oblohu v noci, můžete vidět nesčetné množství hvězd. Ano, pravděpodobně každý z nás slyšel, že ve vesmíru je více hvězd než zrna písku v Sahaře. A vědci z dávných časů se táhli na noční oblohu a snažili se vyřešit hádanky skryté za tou černou prázdnotou. Od starověku mají zdokonalené metody měření prostorových vzdáleností a vlastností hvězdné hmoty (teplota, hustota, rychlost otáčení). V tomto článku budeme hovořit o tom, co je paralaxa hvězd a jak se používá v astronomii a astrofyziky.

Fenomén paralaxy je úzce spjat s geometrií, ale předtím, než zvážíme geometrické zákony, které jsou základem tohoto jevu, ponoříme se do historie astronomie a budeme zkoumat, kdo a kdy objevil tuto vlastnost pohybu hvězd a poprvé ji uplatnil v praxi.

Dějiny

Paralax jako fenomén změny polohy hvězd v závislosti na poloze pozorovatele je již dlouho známý. Více o Galilei Galileo o tom napsal ve vzdáleném středověku. Předpokládal pouze to, že pokud by bylo možné zaznamenat změnu paralaxy pro vzdálené hvězdy, bylo by to důkazem toho Země se točí kolem Slunce, a nikoliv naopak. A bylo to pravda. Nicméně, Galileo to nemohl prokázat kvůli nedostatečné citlivosti tehdejšího zařízení.

Bližší k našim dnům, v roce 1837, Vasilij Yakovlevich Struve vedl řadu experimentů k měření ročního paralaxy pro hvězdu Vega, která je v souhvězdí Lyra. Později byla tato měření považována za nespolehlivou, když v roce následujícího po vydání Struve 1838 Friedrich Wilhelm Bessel změřil roční paralaxu pro hvězdu 61 Cygnus. Proto bez ohledu na to, jak je smutné, zůstává prioritou otevření jednoletého paralaxy Bessel.

Paralax je dnes používán jako hlavní metody měření vzdálenosti od hvězd a dostatečně přesné měřicí zařízení poskytují výsledky s minimálními chybami.

Měli bychom přejít na geometrii dříve, než zvážíme, co je paralaxa. A nejprve si zapamatujme základní pojmy tohoto zajímavého, ačkoli mnoho věd se nelíbilo.

Základy geometrie

Takže to, co potřebujeme vědět z geometrie, abychom pochopili fenomén paralaxy, je to, jak úhly mezi stranami trojúhelníku a jejich délka souvisí.

Nejprve si představte trojúhelník. Má tři spojovací přímky a tři úhly. A pro každý jiný trojúhelník - jeho vlastní úhly a délky stran. Není možné měnit velikost jedné nebo dvou stran trojúhelníku s konstantními hodnotami úhlů mezi nimi, což je jedna ze základních pravd geometrie.

Představte si, že se setkáme s úkolem zjistit hodnotu délky obou stran, pokud známe pouze délku základny a velikost úhlů, které s ní přiléhají. To je možné pomocí jediného matematického vzorce, které spojuje hodnoty délky stran a hodnoty úhlů ležících naproti nim. Takže si představte, že máme tři vrcholy (můžete vzít tužku a nakreslit je), které tvoří trojúhelník: A, B, C. Tvoří tři strany: AB, BC, CA. Pro každý z nich leží úhel: úhel BCA oproti AB, úhel BAC naproti BC, úhel ABC naproti CA.

Vzorec, který spojuje všechna tato šest množství, vypadá takto:

AB / sin (BCA) = BC / sin (BAC) = CA / sin (ABC).

Jak můžeme vidět, všechno není příliš jednoduché. Odkud máme někde sousoší úhlů. Ale jak to můžeme najít? O tom vám řekneme níže.

Základy trigonometrie

Sine je trigonometrická funkce, která určuje souřadnici Y úhlu vyneseného na rovině souřadnic. Abyste to jasně ukázali, obvykle vykreslují rovinu souřadnic se dvěma osami - OX a OY - a označte body 1 a -1 na každém z nich. Tyto body se nacházejí ve stejné vzdálenosti od středu roviny, takže je lze procházet kruhem. Takže máme tzv. Jednotkový kruh. Nyní vytvoříme segment s počátkem na počátku souřadnic a koncem v určitém bodě našeho kruhu. Konec segmentu, který leží na kružnici, má určité souřadnice na osách OX a OY. Hodnoty těchto souřadnic budou kosinus a sinus.

Zjistili jsme, co je sinus a jak ho můžete najít. Ale ve skutečnosti je tato metoda čistě grafická a vytvořila spíše pochopení samotné podstaty toho, co jsou trigonometrické funkce. Může být efektivní pro úhly, které nemají nekonečné racionální hodnoty kosinusu a sinusu. U druhého z nich je účinnější jiný způsob, který je založen na použití derivátů a binomických výpočtů. Říká se tomu série Taylor. Tuto metodu nebudeme považovat, protože je poměrně složitá pro výpočet v mysli. Koneckonců, rychlá práce s počítači je určena pro počítače, které jsou k tomu určeny. Série Taylor se používá v kalkulačích k výpočtu mnoha funkcí, včetně sine, kosinusu, logaritmu a tak dále.

To vše je docela zajímavé a návykové, ale je načase, abychom se pohnuli a vrátili se tam, kde jsme skončili: na úlohu výpočtu hodnot neznámých stran trojúhelníku.

Strany trojúhelníku

Takže zpět k našemu problému: známe dva úhly a stranu trojúhelníku, ke kterému jsou tyto úhly sousední. Potřebujeme znát jen jeden roh a dvě strany. Hledání úhlu se zdá být nejsnadnější: součet všech tří rohů trojúhelníku je 180 stupňů, což znamená, že třetí úhel lze snadno najít odečtením hodnot dvou známých úhlů od 180 stupňů. A znát hodnoty všech tří úhlů a jedné strany, najdeme délky obou stran. Můžete si to sami ověřit na příkladu některého z trojúhelníků.

A teď konečně mluvte o paralaxu jako o způsobu měření vzdálenosti mezi hvězdami.

Paralax

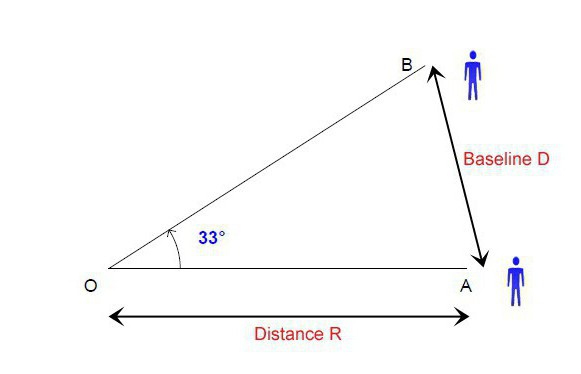
To, jak jsme již zjistili, je jednou z nejjednodušších a nejúčinnějších metod měření mezihvězdných vzdáleností. Paralax je založen na změně polohy hvězdy v závislosti na její vzdálenosti. Například změřením úhlu zjevné polohy hvězdy v jednom bodě oběžné dráhy a potom přímo na její protilehlé straně získáme trojúhelník, ve kterém je známa délka jedné strany (vzdálenost mezi protilehlými body oběžné dráhy) a dva úhly. Odtud budeme moci nalézt dvě zbývající strany, z nichž každá se rovná vzdálenosti od hvězdy na naší planetě v různých bodech její oběžné dráhy. To je metoda, kterou lze vypočítat paralaxu hvězd. A nejen hvězdy. Parallax, jehož efekt je ve skutečnosti velmi jednoduchý, se přesto používá v mnoha jeho variantách v zcela odlišných oblastech.

V následujících částech budeme bližší pohled na rozsah paralaxy.

Cosmos

Hovořili jsme o tom více než jednou, protože paralax je výjimečný vynález astronomů určený k měření vzdáleností hvězd a jiných prostorových objektů. Nicméně to není tak jednoduché. Koneckonců, paralax je metoda, která má své vlastní variace. Například denní, roční a staré paralaxy jsou rozlišeny. Dá se odhadnout, že se všichni liší v časovém intervalu, který prochází mezi kroky měření. Nelze říci, že zvýšení časového intervalu zvyšuje přesnost měření, protože cíle každého typu této metody jsou různé a přesnost měření závisí pouze na citlivosti zařízení a zvolené vzdálenosti.

Denní paralaxy

Denní paralaxa, jejíž vzdálenost je určena úhlem mezi přímkami vedoucími k hvězdě ze dvou různých bodů: střed země a vybraný bod na Zemi. Vzhledem k tomu, že známe rádius naší planety, není složité pomocí hranatého paralaxy vypočítat vzdálenost k hvězdě pomocí matematické metody, kterou jsme dříve popsali. V zásadě se denní paralaxy používají k měření blízkých objektů, například planety, trpasličí planety nebo asteroidy. Pro větší použití použijte následující metodu.

Jeden rok paralaxu

Jednoroční paralaxa je stále stejná metoda měření vzdáleností s jediným rozdílem, že se zaměřuje na měření vzdálenosti k hvězdám. To je přesně případ paralaxy, který jsme uvažovali ve výše uvedeném příkladu. Paralax, určující vzdálenost k hvězce, s pomocí kterého může být zcela přesná, by měla mít jednu důležitou vlastnost: vzdálenost, od které je paralaxa měřena, by měla být větší, tím lépe. Jednoroční paralaxa tuto podmínku splňuje: koneckonců, vzdálenost mezi extrémními body oběžné dráhy je poměrně velká.

Paralax, příklady metod, které jsme zvažovali, jsou jistě důležitou součástí astronomie a slouží jako nepostradatelný nástroj při měření vzdáleností od hvězd. Ve skutečnosti se však dnes používá pouze jeden rok paralaxy, protože diurnal může být nahrazen pokročilejší a rychlejší echolokací.

Jděte dál. Paralax je stále optický fenomén a bylo by zvláštní, kdyby se jeho vlastnosti používaly pouze v astronomii. Existuje další oblast použití tohoto efektu.

Fotografie

Možná nejslavnější typ fotografického paralaxy může být považován za binokulární paralaxu. Pravděpodobně jste si to všimli. Pokud přiložíte prst k vašim očím a zavřete každé oko po sobě, zjistíte, že úhel pohledu na objekt se změní. Totéž se děje při fotografování blízkých objektů. V objektivu vidíme obraz z jednoho úhlu, ale ve skutečnosti bude fotografie vystupovat s trochu jiným úhlem, protože je rozdíl ve vzdálenosti mezi objektivem a hledáčkem (díra, kterou chceme pořídit fotografii).

Než dokončíme tento článek - pár slov o tom, jak může být takový fenomén, jako je optická paralaxa, užitečný, a proč byste se o něm měli dozvědět více.

Proč je to zajímavé?

Za prvé, paralax je jedinečný fyzický jev, který nám dovoluje naučit se hodně o světě kolem nás a dokonce o tom, co je ve stovkách světelných let od něj: Koneckonců, pomocí tohoto jevu je možné vypočítat velikost hvězd.

Jak jsme již viděli, paralax není od nás tak vzdálený fenomén, obklopuje nás všude a s pomocí je vidíme tak, jak je. To je jistě zajímavé a vzrušující, a proto byste měli věnovat pozornost paralaxové metodě, třeba jen zvědavosti. Znalost není nikdy nadbytečná.

Závěr

Takže jsme analyzovali, co je podstatou paralaxy, proč určit vzdálenost k hvězdám, není nutné mít složité vybavení, ale pouze dalekohled a znalost geometrie, jak se používá v našem těle a proč můžeme být tak důležitý v každodenním životě. Doufáme, že poskytnuté informace byly užitečné pro vás!