Pravděpodobnost události Určení pravděpodobnosti události

Zpočátku, být jen sbírkou informací a empirickými pozorováními hry kostky, teorie pravděpodobnosti se stala solidní vědou. První, kdo jí dal matematický rámec, byli Farm a Pascal.

Od myšlení na věčnou teorii pravděpodobnosti

Dvě osobnosti, kterým teorie pravděpodobnosti dluží mnoho základních formulací, Blaise Pascal a Thomas Bayes, jsou známí jako hluboce nábožní lidé, kteří jsou presbyterijským knězem. Zdá se, že touha těchto dvou vědců dokázat, že klamem názoru na určitou Fortune, která štěstí svým mazlíčkům poskytla impuls k výzkumu v této oblasti. Koneckonců ve skutečnosti, jakýkoliv hazard se svými výhrumi a ztrátami je jen symfonií matematických principů.

Díky nadšení kavaléře de Meré, který byl stejně tak hráčem a člověkem, který není lhostejný k vědě, byl Pascal nucen najít způsob, jak vypočítat pravděpodobnost. De Mere se zajímal o takovouto otázku: "Kolikrát musíte házet dvěma kostkami ve dvojicích, aby získali 12 bodů více než 50%?" Druhá otázka, která se velice zajímá o gentlemana: "Jak rozdělit sázku mezi účastníky nedokončené hry?" Samozřejmě, Pascal úspěšně odpověděl na obě otázky de Mere, který se stal nevědomým iniciátorem vývoje teorie pravděpodobnosti. Je zajímavé, že persona de Mere zůstává známá v této oblasti, a ne v literatuře.

Předtím žádný matematik neuskutečnil žádné pokusy o výpočet pravděpodobnosti událostí, protože se předpokládalo, že toto bylo jen rozhodnutí, které říká štěstí. Blaise Pascal dal první definici pravděpodobnosti události a ukázal, že se jedná o specifickou postavu, kterou lze matematicky doložit. Teorie pravděpodobnosti se stala základem pro statistiky a je široce používána v moderních vědách.

Co je to nehoda

Pokud považujeme test, který lze opakovat nekonečně mnohokrát, pak můžeme definovat náhodnou událost. To je jeden z pravděpodobných výsledků experimentu.

Zkušenost je realizace konkrétních akcí v nezměněných podmínkách.

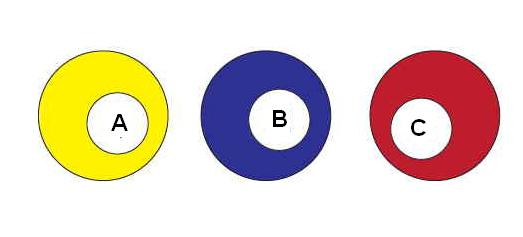
Pro práci s výsledky této zkušenosti jsou události obvykle označovány písmeny A, B, C, D, E ...

Pravděpodobnost náhodné události

Abychom mohli přistoupit k matematické části pravděpodobnosti, je nutné definovat všechny její složky.

Pravděpodobnost události je číselně vyjádřená míra možnosti výskytu určité události (A nebo B) jako výsledek zkušenosti. Označuje pravděpodobnost P (A) nebo P (B).

V teorii pravděpodobnosti rozlišujeme:

• je zaručena spolehlivá událost v důsledku experimentu P (Ω) = 1;
• nemožná událost nikdy nedosáhne P (Ø) = 0;
• náhodná událost spočívá mezi spolehlivou a nemožnou, tj. pravděpodobnost jejího výskytu je možná, ale není zaručena (pravděpodobnost náhodného je vždy v rozmezí 0≤P (A) ≤ 1).

Vztah mezi událostmi

Zvažte jak jeden tak součet událostí A + B, když se událost počítá s realizací alespoň jedné ze složek, A nebo B, nebo obou - A a B.

Ve vztahu k sobě mohou být události:

• Rovná se.
• Kompatibilní.
• Nekompatibilní.
• Opačně (vzájemně se vylučují).
• Závislý.

Pokud se mohou vyskytnout dvě události se stejnou pravděpodobností, jsou stejně tak možné .

Pokud výskyt události A nezruší pravděpodobnost výskytu události B, jsou kompatibilní.

Pokud se události A a B nikdy ve stejné zkušenosti nevyskytují současně, jsou nazývány nekompatibilní . Házení mince je dobrým příkladem: vzhled chvostů je automaticky nezobrazování orla.

Pravděpodobnost součtu takových nekompatibilních událostí se skládá ze součtu pravděpodobností každé události:

P (A + B) = P (A) + P (B)

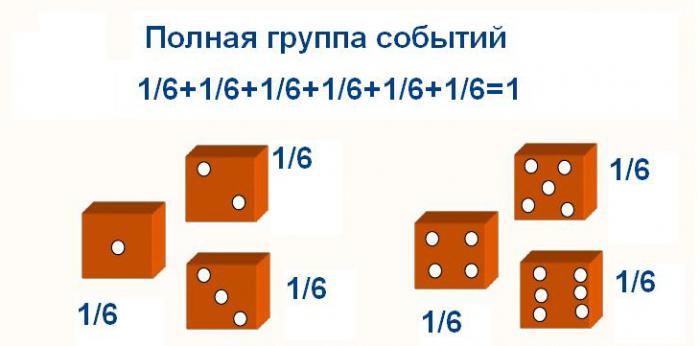
Pokud výskyt jedné události znemožní jiný výskyt, pak se nazývají naproti. Jeden z nich je označen jako A a druhý - A (čteno jako "ne A"). Výskyt události A znamená, že se nenastalo. Tyto dvě události tvoří kompletní skupinu se součtem pravděpodobností 1.

Závislé události mají vzájemný vliv, snižují nebo zvyšují vzájemnou pravděpodobnost.

Vztah mezi událostmi. Příklady

S příklady je mnohem snazší porozumět principům teorie pravděpodobnosti a kombinaci událostí.

Zkušenost, která bude provedena, je vytáhnout koule z krabice a výsledek každého zážitku je základním výsledkem.

Událost je jedním z možných výsledků zážitku - červená koule, modrá koule, míč s číslem šest a tak dále.

Testovací číslo 1. K dispozici je 6 koulí, z nichž tři jsou barevně modré, na ně jsou aplikovány lichá čísla a další tři jsou červené s sudými čísly.

Zkušební číslo 2. K dispozici je 6 modrých koulí s čísly od jednoho do šesti.

Na základě tohoto příkladu můžete volat kombinace:

• Spolehlivá událost. Ve španělštině Událost 2 "Získat modrou kouli" je spolehlivá, protože pravděpodobnost výskytu je 1, protože všechny míčky jsou modré a nemůže být chybět. Zatímco událost "dostat míč s číslem 1" - náhodný.
• Neskutečná událost. Ve španělštině №1 s modrou a červenou kouli událost "dostat fialovou kouli" je nemožná, protože pravděpodobnost jejího výskytu je 0.
• Rovné události. Ve španělštině Počet 1 událostí "dostat míč s číslem 2" a "získat míč s číslem 3" jsou stejně možné a události "dostat míč s sudým číslem" a "dostat míč s číslem 2" mají jinou pravděpodobnost.
• Kompatibilní události. Dva krát za sebou, aby získali šestku v procesu vyhození - to jsou kompatibilní události.
• Nekompatibilní události. V tom isp. Č. 1 události "dostat červenou kouli" a "získat míč s lichým číslem" nelze kombinovat ve stejném zážitku.
• Opačné události. Nejvíce živým příkladem je to, že vrhání mincí, když je tažení orla je ekvivalentní tomu, že nevytahuje ocasy, a součet jejich pravděpodobností je vždy 1 (plná skupina).
• Závislé události . Takže ve španělštině. Č. 1 lze nastavit tak, aby dvakrát za sebou vybíral červenou kouli. Jeho extrakce nebo neextrakce poprvé ovlivňuje pravděpodobnost extrakce podruhé.

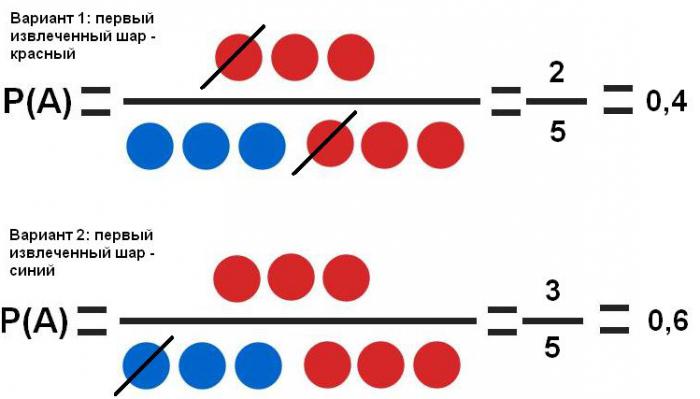
Je vidět, že první událost významně ovlivňuje pravděpodobnost druhého (40% a 60%).

Vzorec pravděpodobnostní události

Přechod od reflexí, které říkají štěstí, přesným datům, se provádí převodem tématu na matematickou rovinu. To znamená, že soudy o náhodné události, jako je "vysoká pravděpodobnost" nebo "minimální pravděpodobnost", mohou být převedeny na konkrétní číselné údaje. Takový materiál je již přípustný pro vyhodnocení, porovnání a vstup do složitějších výpočtů.

Z pohledu výpočtu je určení pravděpodobnosti události poměr počtu základních pozitivních výsledků k počtu všech možných výsledků zkušeností ve vztahu k určité události. Pravděpodobnost je označena písmenem P (A), kde P znamená slovo "pravděpodobite", které je přeloženo z francouzštiny jako "pravděpodobnost".

Takže pravděpodobnost pravděpodobnosti vzorce:

P (A) = m / n,

Kde m je počet příznivých výsledků pro událost A, n je součtem všech možných výsledků pro tuto zkušenost. V tomto případě pravděpodobnost události leží vždy mezi 0 a 1:

0 ≤ P (A) ≤ 1.

Výpočet pravděpodobnosti události. Příklad

Take sp. Č. 1 s kuličkami, jak bylo popsáno výše: 3 modré koule s čísly 1/3/5 a 3 červené s čísly 2/4/6.

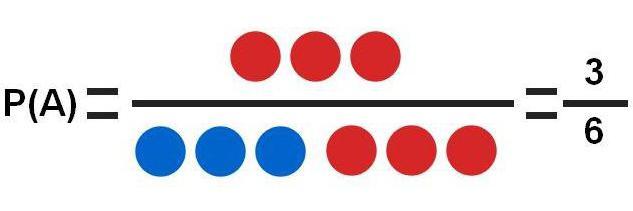
Na základě tohoto testu lze uvažovat o několika různých úkolech:

• A - ztráta červené koule. Existují 3 červené koule a celkem je 6 možností. Jedná se o nejjednodušší příklad, ve kterém pravděpodobnost události je P (A) = 3/6 = 0,5.
• B - ztráta sudého čísla. Celkový počet sudých čísel je 3 (2,4,6) a celkový počet možných číselných variant je 6. Pravděpodobnost této události je P (B) = 3/6 = 0,5.
• C - ztráta čísla větší než 2. Celkem z celkového počtu možných výsledků je celkem 4 takových možností (3,4,5,6). Pravděpodobnost události C se rovná P (C) = 4/6 = 0,67.

Jak je patrné z výpočtů, událost C má větší pravděpodobnost, protože počet pravděpodobně pozitivních výsledků je vyšší než u A a B.

Nekompatibilní události

Takové události se nemohou současně objevit ve stejné zkušenosti. Jako ve španělštině Č. 1 není možné současně dostat modrou a červenou kouli. To znamená, že můžete získat modrou nebo červenou kouli. Stejně tak v kostkách se sudé nemohou objevit současně. liché číslo.

Pravděpodobnost dvou událostí je považována za pravděpodobnost jejich součtu nebo produktu. Součet takových událostí A + B se považuje za takovou událost, která spočívá ve vzhledu události A nebo B a produktu jejich AB - ve vzhledu obou. Například vzhled dvou šestů najednou na tvářích dvou kostek v jednom kotouči.

Součet několika událostí je událostí, která zahrnuje vzhled alespoň jednoho z nich. Vytvoření několika akcí je společným vzorem všech.

V teorii pravděpodobnosti, zpravidla, použití odboru "a" označuje součet, sjednocení "nebo" - násobení. Vzorce s příklady pomohou pochopit logiku přidání a násobení v teorii pravděpodobnosti.

Pravděpodobnost součtu nekonzistentních událostí

Pokud je zvažována pravděpodobnost nekompatibilních událostí, pravděpodobnost součtu událostí se rovná přidání jejich pravděpodobností:

P (A + B) = P (A) + P (B)

Například: vypočítat pravděpodobnost, že v sp. Č. 1 s modrými a červenými koulemi bude vypadat číslo mezi 1 a 4. Nepočítáme v jedné akci, ale součtem pravděpodobností elementárních složek. Takže v této zkušenosti, pouze 6 míčů nebo 6 všech možných výsledků. Čísla, která splňují podmínky, jsou 2 a 3. Pravděpodobnost 2 vypadnutí je 1/6, pravděpodobnost 3 je také 1/6. Pravděpodobnost, že číslo mezi 1 a 4 vypadne, se rovná:

1/6 + 1/6 = 1/3

Pravděpodobnost souhrnu nekompatibilních událostí celé skupiny je 1.

Pokud tedy v experimentu s krychlí přidáme pravděpodobnost, že všechny číslice vypadnou, tak v důsledku toho získáme jednu.

Platí to i pro opakované události, například pro zkušenosti s mincí, kde jedna strana je událostí A a druhá je protějškem, jak je dobře známo

P (A) + P (A) = 1

Pravděpodobnost vzniku nekompatibilních událostí

Násobení pravděpodobností se používá při zvažování výskytu dvou nebo více neslučitelných událostí v jediném pozorování. Pravděpodobnost, že události A a B se objeví současně v ní, je rovna výsledku jejich pravděpodobnosti nebo:

P (A * B) = P (A) * P (B)

Například pravděpodobnost, že v sp. # 1 v důsledku dvou pokusů dvakrát se zobrazí modrá koule, která se rovná

½ * ½ = ¼

To znamená pravděpodobnost události, kdy v důsledku dvou pokusů s extrakcí míčů budou extrahovány pouze modré kuličky, je 25%. Je velmi jednoduché provést praktické experimenty tohoto úkolu a zjistit, zda tomu tak je.

Společné události

Události jsou považovány za společné, když se vzhled jednoho z nich může shodovat s vzhledem druhého. Navzdory tomu, že jsou společné, zvažuje se pravděpodobnost nezávislých událostí. Například házet dvě kostky může dát výsledek, když na oba narazí obr. 6. Ačkoliv se události shodovaly a objevovaly současně, jsou nezávislé na sobě - ​​pouze jedna šestka by mohla spadnout, druhá kost nemá vliv na to.

Pravděpodobnost společných událostí je považována za pravděpodobnost jejich součtu.

Pravděpodobnost součtu společných událostí. Příklad

Pravděpodobnost součtu událostí A a B, které se vzájemně propojují, se rovná součtu pravděpodobností události mínus pravděpodobnost jejich práce (tj. Jejich společná realizace):

R _spoj. (A + B) = P (A) + P (B) - P (AB)

Předpokládejme, že pravděpodobnost, že udeříte cíl jediným výstřelem, je 0,4. Pak událost A - bít cíl v prvním pokusu, B - ve druhém. Tyto události jsou společné, protože je možné, že můžete zasáhnout cíl z prvního a druhého snímku. Ale události nejsou závislé. Jaká je pravděpodobnost výskytu události porážky cíle se dvěma výstřely (nejméně jedna)? Podle vzorce:

0,4 + 0,4-0,4 * 0,4 = 0,64

Odpověď na tuto otázku je: "Pravděpodobnost, že se objeví cíl ze dvou záběrů, je 64%."

Tento vzorec pro pravděpodobnost události může být také aplikován na neslučitelné události, kde pravděpodobnost společného výskytu události P (AB) = 0. To znamená, že pravděpodobnost souhrnu nekonzistentních událostí může být považována za zvláštní případ navrhovaného vzorce.

Pravděpodobnost geometrie pro přehlednost

Je zajímavé, že pravděpodobnost součtu společných událostí může být reprezentována ve formě dvou oblastí A a B, které se navzájem protínají. Jak je zřejmé z obrázku, plocha jejich sdružení se rovná celkové ploše mínus oblast jejich křižovatky. Toto geometrické vysvětlení činí vzorec nelogický na první pohled mnohem srozumitelnější. Všimněte si, že geometrické řešení nejsou v teorii pravděpodobnosti neobvyklé.

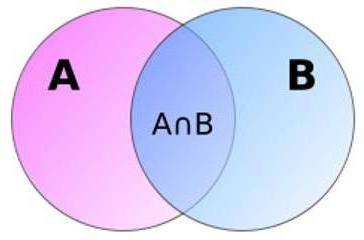
Určení pravděpodobnosti součtu sady (více než dvou) společných událostí je poněkud těžkopádné. Chcete-li jej vypočítat, musíte použít vzorce, které jsou k dispozici pro tyto případy.

Závislé události

Závislé události se nazývají, pokud výskyt jednoho (A) z nich ovlivňuje pravděpodobnost výskytu jiného (B). Kromě toho je zohledněn vliv výskytu události A a jejího nezobrazení. I když jsou události nazývány podle definice, závisí pouze jedna z nich (B). Obvyklá pravděpodobnost je označena jako P (B) nebo pravděpodobnost nezávislých událostí. V případě závislé osoby je zaveden nový koncept - podmíněná pravděpodobnost P _A (B), což je pravděpodobnost závislé události B za předpokladu, že nastala událost A (hypotéza), na níž záleží.

Ale událost A je také náhodná, proto má také pravděpodobnost, že musí a může být vzata v úvahu při provedených výpočtech. Dále bude příklad ukázat, jak pracovat se závislými událostmi a hypotézou.

Příklad výpočtu pravděpodobnosti závislých událostí

Dobrým příkladem pro výpočet závislých událostí může být standardní balíček karet.

Použitím příkladu balíčku 36 karet považujeme za závislé události. Je třeba určit pravděpodobnost, že druhá karta vytažená z balíčku bude mít diamantový oblek, pokud je první karta:

1. Diamanty
2. Další oblek.

Je zřejmé, že pravděpodobnost druhé události B závisí na první A. Proto je-li první možnost platná, že v balíčku byla 1 karta (35) a 1 diamant (8) méně, pravděpodobnost události B:

P _A (B) = 8/35 = 0,23

Pokud je druhá možnost platná, pak je v balíčku 35 karet a celý počet tamburínů (9) je stále zachován, pak pravděpodobnost další události B:

P _A (B) = 9/35 = 0,26.

Je vidět, že pokud je událost A podmíněna skutečností, že první kartou je tamburína, pak pravděpodobnost události B klesá a naopak.

Násobení závislých událostí

Na základě předchozí kapitoly akceptujeme první událost (A) jako fakt, ale pokud chceme v podstatě mluvit, je to náhodné. Pravděpodobnost této události, totiž extrakce diamantů z balíčku karet, se rovná:

P (A) = 9/36 = 1/4

Vzhledem k tomu, že teorie sama o sobě neexistuje, ale má sloužit praktickým účelům, je správné poznamenat, že nejčastěji je zapotřebí, aby vznikly závislost.

Podle věty o produktu pravděpodobností závislých událostí pravděpodobnost výskytu společně závislých událostí A a B se rovná pravděpodobnosti jedné události A vynásobené podmíněnou pravděpodobností události B (v závislosti na A):

P (AB) = P (A) * P _A (B)

Pak v příkladu s balíčkem pravděpodobnost extrakce dvou karet s diamanty je:

9/36 * 8/35 = 0,0571 nebo 5,7%

A pravděpodobnost extrakce na počátku není tamburíny a pak tamburíny, se rovná:

27/36 * 9/35 = 0,19 nebo 19%

Je zřejmé, že pravděpodobnost výskytu události B je větší, pokud je karta obleku odlišná od diamantů nejdříve vytažena. Tento výsledek je zcela logický a srozumitelný.

Celková pravděpodobnost události

Když se problém s podmíněnými pravděpodobnostmi stává vícestranným, nelze jej vypočítat pomocí konvenčních metod. Pokud existují více než dvě hypotézy, jmenovitě A1, A2, ..., A _n , tvoří kompletní skupinu událostí za předpokladu, že:

• P (A _i )> 0, i = 1,2, ...
• A _i ∩ A _j = ∅, i ≠ j.
• Σ _k A = Ω.

Takže vzorec celkové pravděpodobnosti události B s celou skupinou náhodných událostí A1, A2, ..., A _n se rovná _:

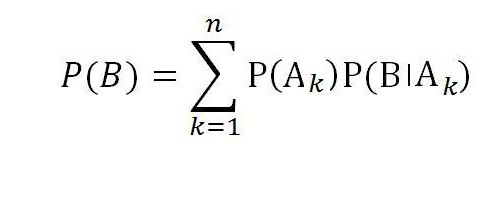
Pohled do budoucnosti

Pravděpodobnost náhodných událostí je nezbytná v mnoha oblastech vědy: ekonometrie, statistika, fyzika atd. Jelikož některé procesy nelze určit deterministicky, jelikož jsou samy o sobě pravděpodobnostní, je zapotřebí speciálních metod práce. Teorie pravděpodobnosti události může být použita v jakémkoli technologickém poli jako způsob, jak určit možnou chybu nebo poruchu.

Můžeme říci, že uznáváme pravděpodobnost, že nějakým způsobem přijímáme teoretický krok do budoucnosti a zkoumáme to přes hranice vzorců.