Rychlé řazení je jedním z nejlepších třídících metod.

Pokud programujete a váš kód překračuje rámec psaní kalkulačky, často se setkáte nebo budete konfrontováni s potřebou třídit určitou řadu dat. Existuje mnoho způsobů řazení. V tomto článku budeme analyzovat hlavní z nich a zaměříme se na rychlé třídění.

Rychlý koncept řazení

Rychlé řazení - Rychlé řazení nebo qsort. Jménem je jasné, co to je a proč. Ale pokud to není jasné, pak to je algoritmus Rychlou řadou pole má algoritmus v průměru O (n log n) účinnost. Co to znamená? To znamená, že průměrná doba provozu algoritmu se zvyšuje po stejné trajektorii jako graf této funkce. Některé populární jazyky obsahují vestavěné knihovny s tímto algoritmem a to již naznačuje, že je velmi efektivní. Jedná se o jazyky jako Java, C ++, C #.

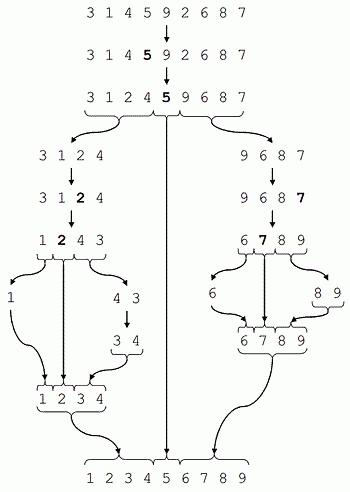
Algoritmus

Metoda rychlého řazení používá rekurze a strategii "Divide and Conquer".

1. V poli, hledáme určitý podpůrný prvek, pro jednoduchost je lepší vzít centrální, ale pokud chcete pracovat na optimalizaci, budete muset vyzkoušet různé možnosti.

2. Vlevo od podpěry se hledá větší prvek než referenční, vpravo, menší prvek než referenční, pak je vyměníme. Proveďte to, dokud není maximální vpravo nižší než minimum vlevo. Všechny drobné elementy jsou proto hozeny na začátek, velké - až do konce.

3. Rekurzivně aplikujte tento algoritmus na levou a pravou část našeho algoritmu samostatně, pak znovu a znovu, až dosáhne jednoho prvku nebo určitého počtu prvků. Jaký je tento počet prvků? Existuje další způsob optimalizace tohoto algoritmu. Když se tříděná část přibližně rovná 8 nebo 16, může být zpracována obvyklým tříděním, například třídou bublin. Takže zvýšíme efektivitu našeho algoritmu od té doby nezpracovává malé pole tak rychle, jak bychom chtěli.

Celé pole bude tedy zpracováno a tříděno. A teď budeme vizuálně studovat tento algoritmus.

Rychlá účinnost řazení

Rychle třídíte nejrychlejší třídící algoritmus? Určitě ne. Nyní je stále více a více třídění, v současné době nejrychlejší třídění je Timsort, funguje to extrémně rychle pro pole, která byla původně tříděna jinak. Ale nezapomeňte, že metoda rychlého řazení je jednou z nejjednodušších, která je napsána, je to velmi důležité, protože jednoduchý projekt zpravidla vyžaduje jednoduchý pravopis a ne obrovský algoritmus, který sám nemůžete psát. Timsort není také nejsložitějším algoritmem, ale ten nejjednodušší není pro něj přesně lesk.

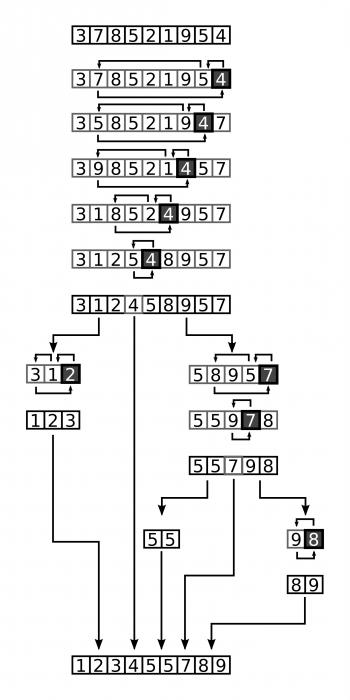
Implementace algoritmu

No, dostali jsme se do "lahodného". Nyní se podívejme na to, jak je tento algoritmus implementován. Jak již bylo zmíněno dříve, není to příliš komplikované, spíše snadné. Ale stále provádíme úplnou analýzu všech kroků našeho kódu, abyste pochopili, jak rychlé třídění funguje.

Naše metoda se nazývá quickSort. Spouští hlavní algoritmus, ve kterém přenášíme pole, jeho první a poslední prvky. Zapisujeme do proměnných i a k ​​prvního a posledního prvku tříděného segmentu, abychom nezměnili tyto proměnné, protože je potřebujeme. Poté zkontrolujeme vzdálenost mezi prvním a posledním zkontrolovaným: je větší nebo rovna jedné? Pokud ne, pak jsme se dostali do centra a musíme se dostat z třídění tohoto segmentu, a pokud ano, pokračujeme v třídění.

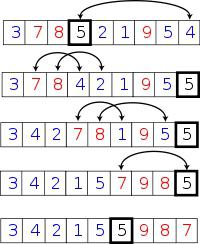
Potom vezmeme první prvek v segmentu, který je tříděn pro nosný prvek. Uděláme další cyklus, dokud se nedostaneme do centra. V tom činíme dva další cykly: první je pro levé a druhé pro pravé. Provádíme je tak dlouho, dokud existují prvky, které odpovídají danému stavu, nebo dokud nedosáhneme prvek podpory. Potom, pokud je minimální prvek stále vpravo a maximum je vlevo, vyměňte je. Po ukončení cyklu změňte první prvek a odkaz, pokud je odkaz menší. Potom rekurzivně vytvoříme náš algoritmus pro pravou a levou část pole, a tak pokračujeme, dokud nedosáhneme segment o délce 1 prvku. Potom se vrátí všechny rekurzivní algoritmy a úplně opustíme třídu. Také v dolní části je metoda swapu - zcela standardní metoda při řazení řady náhrad. Aby nebylo několikrát zapisováno nahrazení prvků, zapíšeme jednou a změníme prvky v tomto poli.

Závěrem lze říci, že pokud jde o poměr kvality a složitosti, rychlé řazení je na předních pozicích mezi všemi algoritmy, takže byste si měli určitě uvědomit tuto metodu a v případě potřeby ji použít ve svých projektech.