Jednoduchý úkol: jak najít obvod?

Znalosti o tom, jak najít obvod, studenti získají více na základní škole. Poté se tyto informace neustále používají v průběhu matematiky a geometrie.

Obecná teorie pro všechny postavy

Strany jsou obvykle označovány latinkou. Kromě toho mohou být označeny jako segmenty. Pak jsou pro obě strany vyžadována dvě písmena a velká písmena. Nebo zadejte označení jednoho písmena, které je určitě malé.
Písmena jsou vždy vybrána abecedně. Pro trojúhelník budou první tři. Šestiúhelník bude mít 6 z nich - od a do f. To je vhodné pro zavedení vzorců.

Nyní, jak najít obvod. Je to součet délky všech stran této postavy. Počet položek závisí na typu. Obvod je označen latinkou R. Jednotky měření se shodují s hodnotami uvedenými pro strany.

Formule obvodů různých tvarů

Pro trojúhelník: P = a + b + c. Je-li to isosceles, pak je vzorec převeden: P = 2a + c. Jak najít obvod trojúhelníku, pokud je rovnostranný? Pomůže to: P = 3a.

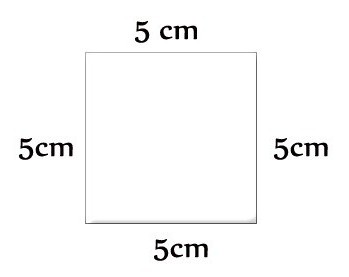
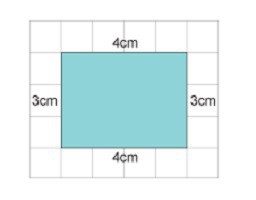
Pro libovolný čtyřúhelník: P = a + b + c + d. Jeho zvláštním případem je čtverec, obvodový vzorec: P = 4a. Existuje obdélník, pak je nutná následující rovnost: P = 2 (a + b).

Co když délka jedné nebo více stran trojúhelníku není známa?

Využijte kosinová věta pokud existují dvě strany dat a úhel mezi nimi, který je označen písmenem A. Potom, než objevíte obvod, budete muset vypočítat třetí stranu. Pro tento účel je užitečný následující vzorec: s2 = a2 + v2 - 2 v cos (A).

Zvláštní případ této věty je formulován Pythagorasem pravý trojúhelník. V něm se hodnota kosinusu pravého úhlu stává nulou, což znamená, že poslední termín jednoduše zmizí.

Tam jsou situace, kdy se naučit, jak najít obvod trojúhelníku může být na jedné straně. Současně jsou však také známé rohy postavy. Zde se sínusová věta dostane k záchraně, když poměr délky stran k sinům odpovídajících protilehlých úhlů je stejný.

V situaci, kdy obvod čísla musí být rozpoznán oblastí, další vzorce budou užitečné. Pokud je například známa poloměr zapsaného kruhu, pak je otázka, jak najít obvod trojúhelníku, následující užitečný vzorec: S = p * r, zde p je poloprůchod. Musí být odvozeno z tohoto vzorce a vynásobeno dvěma.

Příklady úkolů

Stav prvního. Zjistěte obvod trojúhelníku, jehož strany jsou 3, 4 a 5 cm.
Rozhodnutí. Je nutné použít rovnici, která je uvedena výše, a nahradila data do problému s hodnotou. Výpočty jsou snadné, vedou k počtu 12 cm.
Odpověď zní. Obvod trojúhelníku je 12 cm.

Druhá podmínka. Jedna strana trojúhelníku je 10 cm. Je známo, že druhý je o 2 cm větší než první a třetí je 1,5 krát větší než první. Je nutné vypočítat jeho obvod.
Rozhodnutí . Abyste se naučili, musíte počítat dvě strany. Druhý je určen jako součet 10 a 2, třetí se rovná produktu 10 a 1,5. Pak zůstane pouze počítat součet tří hodnot: 10, 12 a 15. Výsledek bude 37 cm.
Odpověď zní. Obvod je 37 cm.

Stav třetího. K dispozici jsou obdélník a čtverec. Jedna strana obdélníku je 4 cm a druhá 3 cm delší. Je třeba vypočítat hodnotu strany čtverce, pokud je jeho obvod o 6 cm menší než obdélník.
Rozhodnutí. Druhá strana obdélníku je 7. Je-li to známo, je snadné vypočítat jeho obvod. Výpočet dává 22 cm.
Chcete-li najít stranu čtverce, musíte nejprve odečíst 6 od obvodu obdélníku a potom rozdělit výsledné číslo o 4. V důsledku toho máme číslo 4.
Odpověď zní. Boční čtverec 4 cm.