Koncepce úhlové hybnosti, její zákon o ochraně přírody a příklad řešení problému

Rotující pohyb není o nic méně obvyklý než lineární pohyb objektů. Aby to bylo ověřeno, stačí připomenout rotaci kol vozů a jízdních kol, lopatky vrtulníků a ventilátorů, planety kolem své osy a kolem hvězd. Pro popis procesu kruhového pohybu objektů se používá fyzikální veličina, která se nazývá "moment hybnosti". Zvažte v článku, co to je.

Momentový moment částic a osa otáčení

Níže je výkres, který schematicky ukazuje, že částice nebo materiálová hmota m se pohybují po kruhové trajektorii o poloměru ¯ s tangenciální rychlostí. Osa rotace je kolmá na rovinu obrázku v bodě O.

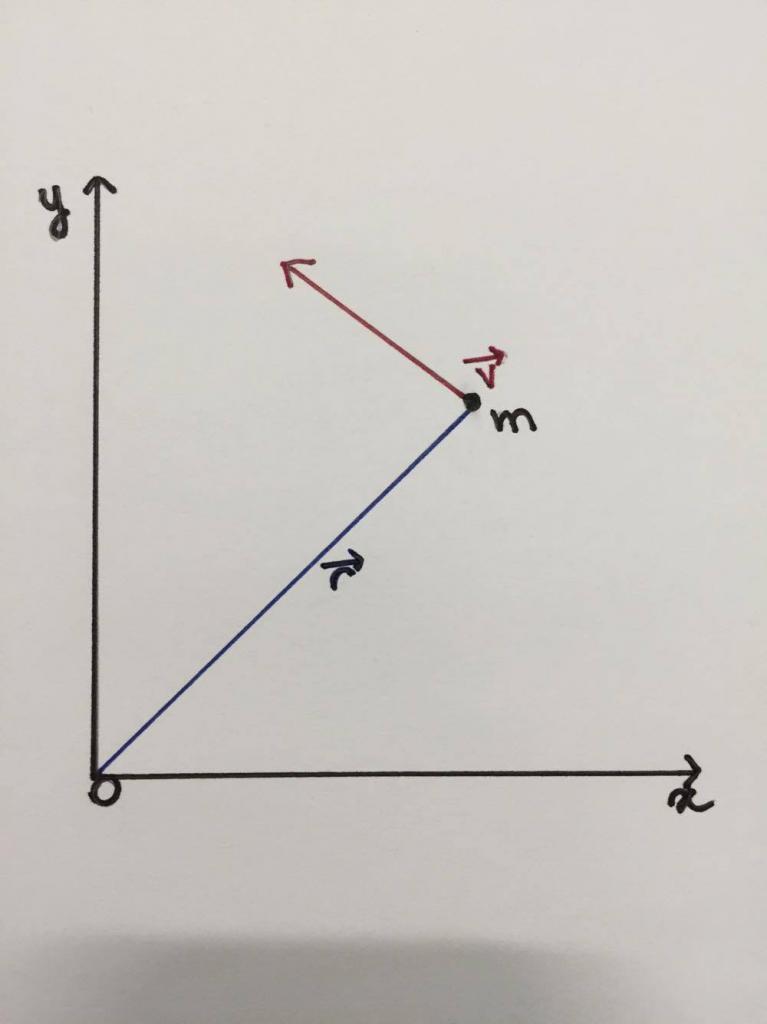
Představujeme následující fyzikální množství:

L¯ = r¯ * m * v¯ = r¯ * p¯.

Říká se to momentu hybnosti nebo momentu hybnosti. Jak vidíte, je to vektorová veličina. Jeho směr může být určen pravidlem pravé ruky: je třeba směrovat 4 prsty tak, že se pohybují podél vektoru r¯, přicházejí na konec vektoru p¯ (nebo v¯), pak palec zobrazí směr L¯. V tomto případě je L¯ směrován do čtečky kolmo k rovině výkresu.

Vzhledem k tomu, že rychlost částic (hybnost) na obrázku je nasměrována v pravém úhlu k vektoru ¯, redukovaná rovnice může být přepsána v skalární podobě:

L = r * m * v = r * p.

Úhlová rychlost a moment setrvačnosti

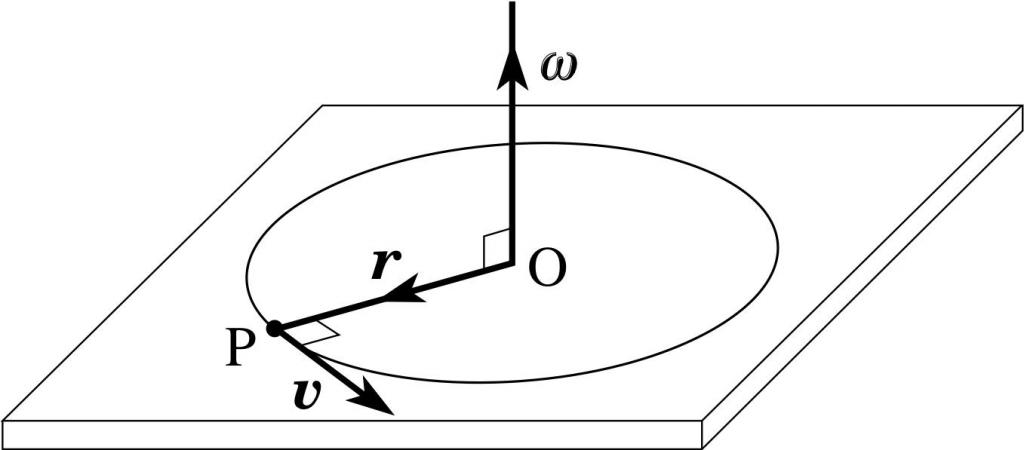
Momentum částice z předchozího příkladu lze zapsat úhlovou rychlostí ω. K tomu použijeme jeho spojení s lineární rychlostí:

ω = v / r => v = ω * r.

Nahrazením poslední rovnice do skalární rovnice pro L získáme:

L = r ² * m * ω = I * ω, kde I = r ² * m.

Zde je moment setrvačnosti částice. Výsledný výraz se často používá k řešení praktických problémů, z nichž jedna bude popsána níže.

Zákon o zachování rotačního pohybu

Pohyb v kruhu a lineární pohyb objektů ve vesmíru jsou charakterizovány ochrannými zákony. Jedním z nich je zachování momentu hybnosti. Tento zákon dostáváme.

Rovnice zvažovaného druhu pohybu má následující podobu:

dL / dt = M.

Kde dL / dt charakterizuje změnu momentu hybnosti tělesa v čase, když je ovlivněn určitým momentem M vytvořeným vnějšími (nikoli vnitřními) silami. Pokud je tento moment síly nulový, pak levá strana výrazu zmizí, což znamená L = const. Pro tento případ můžeme napsat následující rovnost:

L = konstanta = I ₁ * ω ₁ = I ₂ * ω ₂ .

Co znamená tento záznam? Říká se, že jestliže se nějaké tělo otáčí rychlostí ω ₁ a má setrvačný moment I ₁ , pak díky některým vnitřním (nikoliv vnějším) silám změní moment setrvačnosti a stane se rovno I ₂ , pak bude nová rychlost otáčení ω ₂ proporcionální s touto změnou.

Zaznamenaný vztah se nazývá zákon zachování momentu hybnosti bodu (těla) analogicky s odpovídajícím zákonem pro lineární veličiny (zachování hybnosti), protože moment setrvačnosti hraje roli hmoty a úhlová hodnota ω hraje roli hmoty.

Použití zákona L = const

Vztah uvedený v předchozím odstavci lze vidět v akci, když bruslaři nebo balerínají. Vykonávají komplexní akrobacii, otáčejí tělem, rozptylují si paže a nohy a pak přitisknou končetiny na tělo. Poslední akce vede k poklesu hodnoty I a tím k nárůstu rychlosti otáčení, což vytváří spíše velkolepý efekt.

Dalším příkladem použití neměnnosti momentu hybnosti systému je realizace rotace umělé družice ve vesmíru. Chcete-li to provést, spusťte na něj speciální setrvačník. Vzhledem k tomu, že celková momentová hybnost by se neměla měnit v důsledku působení vnitřních sil, samotný satelit se začne otáčet v opačném směru. Jakmile se otočí na požadovaný úhel kolem své osy, setrvačník se zastaví pomocí elektrického motoru a tělo družice také zastaví jeho otáčení.

Vypočítejte moment setrvačnosti

Jelikož hodnota I je přítomna v zákoně o ochraně kruhového pohybu, měli bychom o něm říci pár slov. To charakterizuje setrvačnost systému, to je, jak to "těžké" nebo "snadné" rozpoutat. Například zotrvačník automobilu má velkou hmotnost a relativně velký poloměr, takže jeho moment setrvačnosti je významný. Na rozdíl od toho je kolo kola vyrobeno z hliníkového světelného ráfku, takže pro něj budu poměrně malý.

Pro výpočet této fyzikální charakteristiky použijte vzorec:

I = ∫ _m (r ² * dm).

Odkud je vidět, že moment setrvačnosti je charakteristickým znakem systému, do něhož vstoupí tělo revoluce, a ne samotné tělo. Tento fakt rozlišuje I od lineární setrvačnosti, která závisí pouze na vlastnostech těla (jeho hmotnost).

Úloha s otočnou tyčí

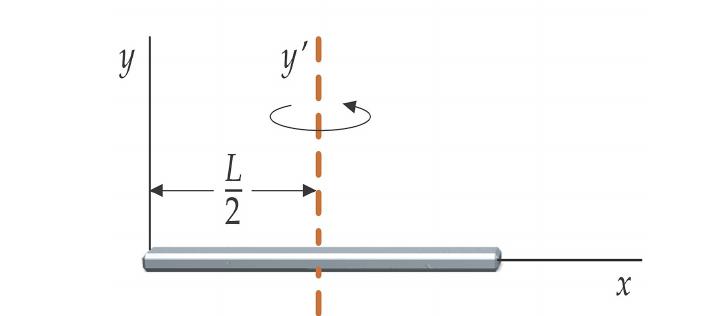
Vyřešíme zajímavý problém: existuje tuhá tyč, která se otáčí kolem osy umístěné na jejím konci. Pokud je tato osa plynule posunuta do středu hmotnosti tyče, jak se změní její rychlost otáčení?

Jedná se o klasický úkol uplatňovat zákon o zachování momentu hybnosti. Obtíž spočívá v výpočtu změny momentu setrvačnosti. K tomu můžete použít výše uvedený vzorec s integrálem, ale bude snadnější se podívat na potřebné hodnoty I v referenční literatuře.

Na začátku procházela osa otáčení přes konec tyče. Pro tento systém se moment setrvačnosti rovná:

I ₁ = m * L 2/3, kde L je délka tyče, m je její hmotnost.

Když byla osa posunuta do středu hmoty objektu, jeho moment setrvačnosti se změnil, stalo se rovno:

I ₂ = m * L 2/12.

Použijte zákon o ochraně pro L, získáme:

m * L 2/3 * ω ₁ = m * L 2/12 * ω ₂ => ω ₂ / ω ₁ = m * L 2/3 / (m * L 2/12) = 4.

Dostali jsme odpověď na problém: tyč se bude otáčet čtyřikrát rychleji než na začátku.