Koncepce matice a základní definice

Takový koncept jako matice se používá a objevuje se v sekcích vyšší matematiky. Nejčastěji se nachází v systému lineárních rovnic. Tak jaký je základní pojem matice? Abychom to pochopili, není nutné být matematickým géniem.

Matrix je systém čísel mn, který je v matematice napsán ve formě tabulek, ve kterých m jsou řádky a n jsou sloupce. Na jeho křižovatce jsou prvky. Velikost matice závisí na počtu řádků a sloupcích.

Zpočátku byla zvažována trojúhelníková matice, ale není vhodná pro řešení složitých rovnic, proto se v matematice používá obdélníkový analog. Takový systém je považován za vhodný k řešení problému.

Odkud pochází matice

Když hovoříme o první zmínce, pojetí matice pochází z Číny, nebo spíše bylo spojeno s "magickými čtverci". Tyto stoly byly považovány za amulety kvůli číslům na nich napsaných. V té době neexistovala ani samotná koncepce matice, ani způsoby, jak to vyřešit. V některých kmenů určila stupeň příbuznosti, aby lidé zjistili, zda se mohou oženit nebo ne.

Ale samotný koncept byl představen na počátku 19. století Jamesem Sylvesterem, který byl matematikem angličtiny. Různí vědci pracovali na teorii matric, vytvářeli komplex řešení pro složité algebraické problémy.

Matrix a její hlavní typy

Takže dříve byla zvažována koncepce matice. Typy matic jsou uvedeny níže:

• Malé Jedná se o jeden řádek, tj. Tento typ matice má počet řádků přesně m = 1, ale počet jeho sloupců je libovolný.
• Sloupec. Tato odrůda se skládá pouze z jednoho sloupce, ale může obsahovat i několik řádků. Pro tento druh matice má svůj vlastní univerzální vstup. Označuje, že položky, které jsou v závorkách, by měly být zapsány jako sloupec. Navíc ušetří nejen prostor, ale i čas.
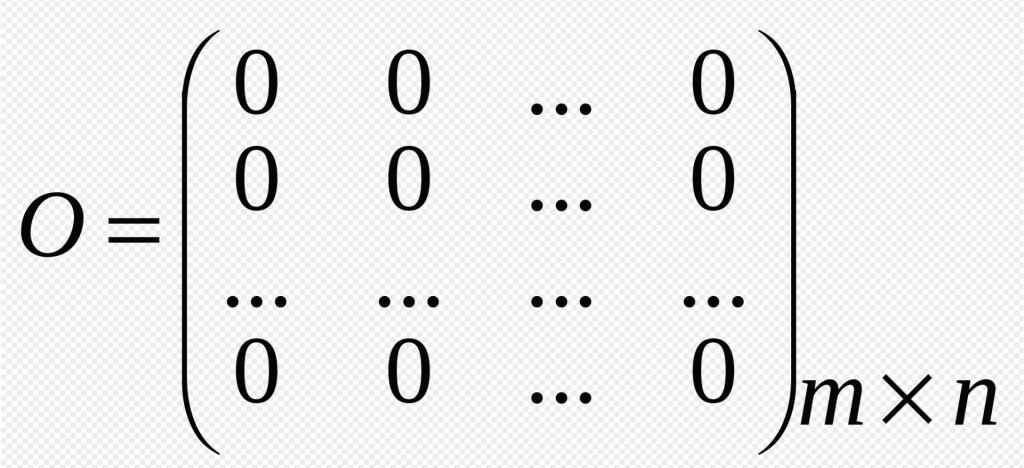
• Nulová matice Tento formulář existuje, když jsou všechny jeho prvky rovny 0. Označují tento typ matice "O" Tento prvek také dostal své jméno vzhledem k tomu, že v počtu má podobné funkce s nulou v teorii čísel.
• Náměstí. Tento typ matice je nejčastější, jeho rozdíl spočívá v tom, že má stejný počet sloupců a řádků. Když jsou na různých koncích sloupce připojeny dva prvky, dostaneme hlavní diagonádu. V tomto ohledu je diagonální stůl rozdělen na několik systémů:

a) Diagonální. Tento typ čtvercové matice, který neobsahuje prvky patřící k hlavní diagonále.

b) Jeden. Tento typ úhlopříčky se skládá pouze z jedné jednotky. Každá taková matice je skalární.

c) Skalární. Toto je typ, kde se hlavní diagonála skládá ze stejného čísla.

d) Šipka. Jedná se o druh čtvercové matice, ve které téměř všechny prvky jsou nulové, ale složky, které tvoří první sloupec, stejně jako ty, které se vztahují k úhlopříčce a první řadě, se jí nerovná.

• Binární Tento typ tabulky obsahuje nuly a ty.
• Pascalova matice - v tomto typu matice se všechny prvky skládají z čísel patřících k trojúhelníku stejného jména.
• Tridiagonální V tomto typu matice jsou nenulové prvky umístěny na třech diagonálech, mezi něž patří hlavní a ty nad a pod.

Pořadí matice

Poté, co jsme se dozvěděli, že má různé typy, je třeba říci o následujícím pojmu: hodnost matice. Tím se míní počet nezávislých lineárních sloupců nebo počet nezávislých lineárních řádků. Také hodnost každé matice je pořadí nezletilých, což je nejvyšší, její determinant je nenulový.

Pořadí je označeno číslem A, ale je nalezena pozice A. Obě koncepty jsou považovány za správné, takže s různými pravopisy to nebude považováno za chybu. Nejdůležitější je nezapomenout, že řada řádků je vždy stejná jako hodnost sloupců.

Akce na matici

Matrix je univerzální systém pro řešení algebraických problémů, na něm jsou prováděny různé akce. Ty zahrnují násobení dvou matic, doplnění, násobení číslem a dalšími maticemi.

Provádění četných akcí v algebru, systém různých matric pomáhá najít snadnější způsob řešení problémů. Vyžaduje méně času a pomáhá neztratit v mnoha činnostech.

Operace související s maticí se používají nejen v matematice, ale i ve fyzice a chemii.