Fenomén lomu. Úhly lomu a pádu. Zjevná hloubka nádrže
Fenomén lomu je vizuální efekt, který nastává, když světelný paprsek překročí rozhraní mezi dvěma průhlednými médii. Důležitými vlastnostmi tohoto efektu jsou indexy lomu a úhly dopadu a lomu. V tomto článku bližší popisujeme tohoto optického jevu.
Snellův zákon pro fenomén lomu
Jak víte, každá vlna, včetně elektromagnetické, se šíří rovnoměrně a konstantní rychlostí v homogenním materiálu. Jakmile dojde k porušení homogenity tohoto materiálu, změní vlna svou přímočarou trajektorii. Živým příkladem takové změny je refrakce světla.
Refrakce paprsku se objevuje v lokalizovaném bodě v prostoru, který je umístěn na rozhraní dvou průhledných médií s různými fyzikálními vlastnostmi. Prostředí může být například sklo, vzduch, voda, průhledný plast a další. Když narazí na druhé médium, světlo se odchyluje od určitého úhlu od původní trajektorie.
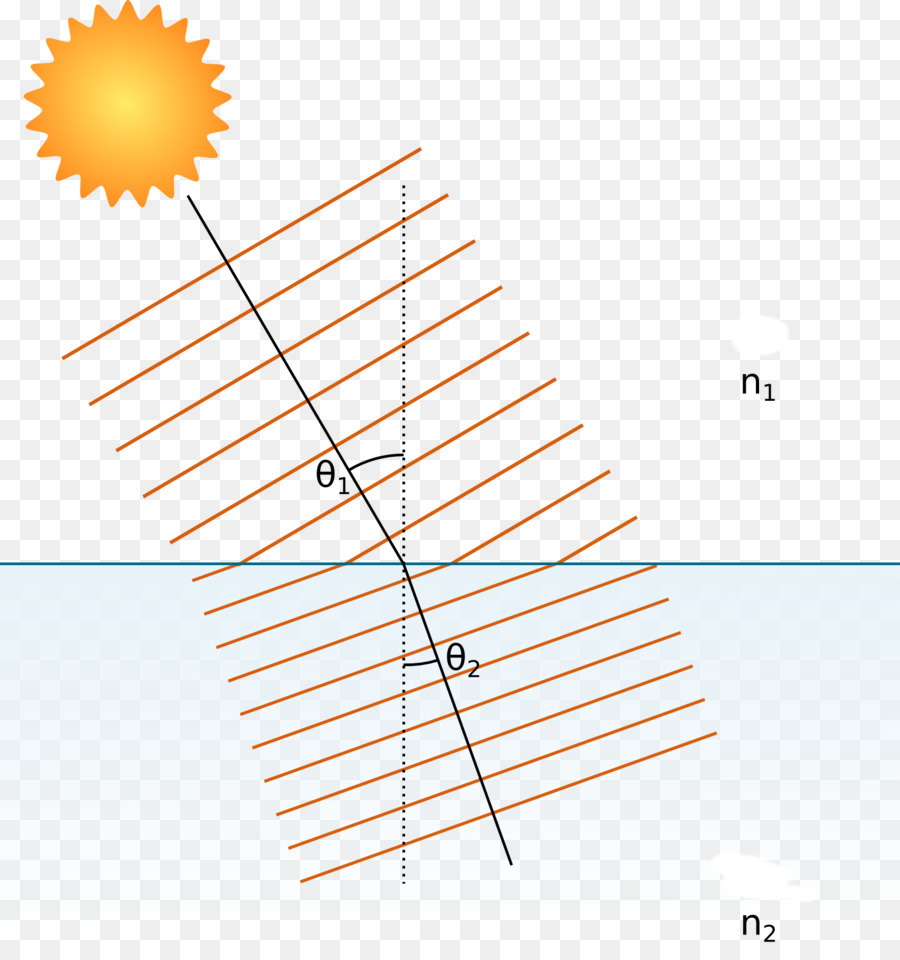
Pokud psychicky nakreslíte kolmici přes bod, kde paprsek protíná rovinu dělícího média a určíte úhel mezi kolmicí a paprskem jako θ 1 a úhel mezi stejnou kolmicí a paprskem, který prošel do druhého média jako θ 2 , platí následující vztah:
sin (θ 1 ) * n 1 = sin (θ 2 ) * n 2
Úhly theta jedna (θ 1 ) a theta two (θ 2 ) se nazývají úhly dopadu a refrakce. Hodnoty n1, n2 jsou důležité optické vlastnosti prvního a druhého média, nazývají se refrakčními indexy.
Výše uvedený vzorec se nazývá Snellův zákon (Snellius), protože holandský vědec Willebrord Snellus na počátku XVII. Století jej poprvé formuloval ve své moderní podobě a analyzoval velké množství experimentálního materiálu.

Index lomu
Podle matematické definice této fyzické veličiny se rovná poměru dvou rychlostí světla: ve vakuu a v materiálu, to znamená:
n = c / v
Protože c> v, pak n bude vždy větší než jedna.
Index lomu má různé hodnoty pro různé látky. Například pro vzduch se téměř rovná 1 a pro vodu je 1,33. Hodnota n závisí také na chemickém složení stejného materiálu. Například index lomu skla závisí na druhu skla a pohybuje se od 1,5 do 1,66.
Kromě vlastností materiálu se n výrazně liší, pokud změníte frekvenci světla v paprsku. Úhel refrakce modrého světla je vždy větší než červená. Údaje uvedené v předchozím odstavci se týkají žluté části spektra viditelné člověkem (λ ≈ 590 nm).
Optická hustota média
Tato fyzická charakteristika určuje, jak silně médium zpomaluje rychlost světla. Optická hustota je jednoznačně určena indexem lomu. Například voda je opticky hustší než vzduch a jakýkoliv druh skla je hustší než voda.
Pokud se podíváte na recepturu Snell, můžete vidět, že čím větší je optická hustota média, tím nižší je úhel k normálu. Tento závěr platí bez ohledu na to, ze kterého média a do jakého světla paprsek padne. Takže při zohlednění hranice vody a vzduchu bude úhel refrakce menší, než je úhel dopadu, pokud se paprsek dostane do vody. Změníte-li směr paprsku, bude úhel dopadu menší.
Výzva uplatnění Snellova zákona
Je známo, že paprsek světla dopadá na vodní hladinu pod úhlem 32 ° . Je nutné určit úhel refrakce světla, stejně jako velikost jeho změny, pokud zvýšíte úhel dopadu o 10 ° .
Množství refrakce světla může být stanoveno Snellovým zákonem. Máme:
θ 2 = arcsin (sin (θ 1 ) * n 1 / n 2 )
Protože světlo klesne ze vzduchu do vody, pak n 1 = 1 a n 2 = 1,33. Vědomí, že θ 1 = 32 o , získáváme:
θ 2 = arcsin (sin (32 o ) * 1 / 1,33) = 23,48 o
Jak vidíte, úhel se výrazně snížil. Nyní vypočítáme úhel refrakce nosníku, jestliže θ 1 = 42 o . Pomocí stejného vzorce získáváme:
θ 2 = arcsin (sin (42 o ) * 1 / 1,33) = 30,21 o
Rozdíl mezi získanými úhly získáme:
30,21 o - 23,48 o = 6,73 o
Získaný výsledek znamená, že změny mezi úhly dopadu a lomu nejsou lineární. Zvýšení úhlu dopadu o 10 ° vedlo ke změně úhlu refrakce pouze o 6,7 ° .
Úloha určení zjevné hloubky

Mnozí si všimli, že pokud se podíváte na dno nádrže, kameny ležící na ní a rostoucí řasy se zdájí blízko povrchu. Vypočítejte pomocí zákona lomu, jak se skutečné a zřejmé hloubky navzájem liší. Za tímto účelem budeme zvažovat malé úhly dopadu, to znamená, že pozorovatel vypadá svisle dolů na dno nádrže. Níže je odpovídající obrázek.
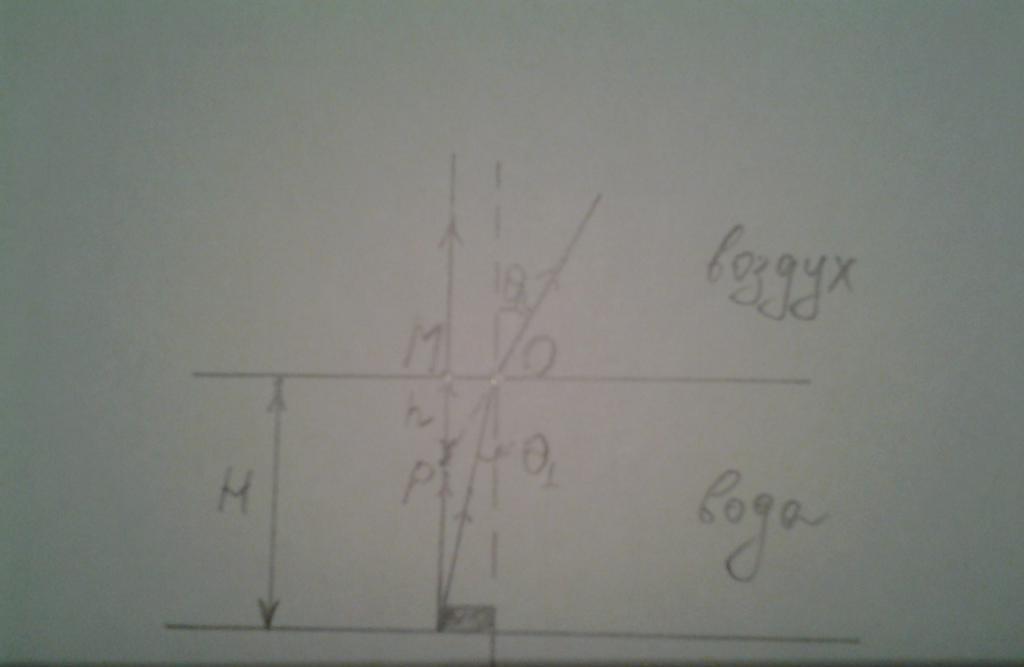
Na obrázku je zobrazen objekt ležící na dně. Vzhledem k tomu, že dva paprsky, které vycházejí ze stejného bodu objektu, protínají v bodě P pozorovatele, bude hloubka h = MP zřejmá.
Chcete-li najít h, zvažte správný trojúhelník POM. Interval MO je H * tg (θ 1 ), úhel POM je 90 - θ2. Nyní můžete napsat:
tg (90-θ2) = h / (H * tg (θl))
Vzhledem k tomu, že tečna je rovna poměru sinus k kosinusu a pomocí vzorce pro trigonometrické funkce, můžeme tuto rovnost přepisovat následujícím způsobem:
cos (θ 2 ) / sin (θ 2 ) = cos (θ 1 ) * h / (H * sin (θ 1 ))
Vzhledem k tomu, že zvažujeme malé úhly (blízké vertikálnímu bodu), budou kosiny téměř stejné jako jednotky, takže poslední vzorec bude zjednodušen do podoby:
h = h * sin (θ 1 ) / sin (θ 2 )
Ale poměr sinů je roven inverznímu poměru indexů lomu médií podle zákona Snell, proto zapisujeme:
h = H * n 2 / n 1
Jak se paprsek posouvá z vody, n2 je indikátorem pro vzduch, který se rovná jednomu. Poslední vzorec pro zdánlivou hloubku nádrže při vertikálním pohledu je:
h = h / n, kde n = 1,33
Takže zdánlivá hloubka je přibližně o 25% menší než skutečná.