Trojrozměrný prostor: vektory, souřadnice

Dokonce i ze školního kurzu algebry a geometrie víme o konceptu trojrozměrného prostoru. Pokud chápeme, termín "trojrozměrný prostor" je definován jako souřadnicový systém se třemi dimenzemi (každý to ví). Ve skutečnosti je možné popsat libovolný objemový objekt pomocí délky, šířky a výšky v klasickém smyslu. Nicméně, jak říkají, pojďme trochu hlouběji.

Co je trojrozměrný prostor

Jak již bylo zřejmé, pochopení trojrozměrného prostoru a objektů schopných existovat uvnitř je určeno třemi hlavními koncepty. Je pravda, že v případě bodu jsou přesně tři hodnoty a v případě přímých, zakřivených, zlomených čar nebo objemových objektů mohou být odpovídající souřadnice větší.

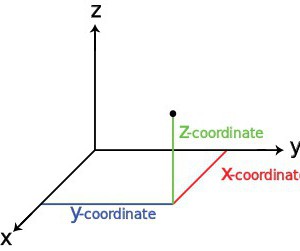
V tomto případě vše závisí na typu objektu a použitém souřadnicovém systému. Dnes je považován za nejběžnější (klasický) kartézský systém, někdy také nazývaný obdélník. Ona a některé další druhy budou diskutovány později.

Mimo jiné zde je třeba rozlišovat mezi abstraktními pojmy (pokud je to možné říct beztvaré) jako body, přímky nebo roviny a postavy, které mají konečné rozměry nebo dokonce objem. Pro každou z těchto definic existují také vlastní rovnice popisující jejich možné umístění v trojrozměrném prostoru. Ale teď o tom není.

Koncepce bodu v trojrozměrném prostoru

Nejprve definujeme, co je bod v trojrozměrném prostoru. Obecně lze jej nazvat určitou základní jednotkou, která definuje jakoukoli plochou nebo trojrozměrnou postavu, čáru, segment, vektor, rovinu apod.

Samotný bod je charakterizován třemi hlavními souřadnicemi. Pro ně jsou v pravoúhlém systému používány speciální vodítka nazývané osy X, Y a Z, první dvě osy slouží k vyjádření horizontální polohy objektu a třetí se týká vertikální specifikace souřadnic. Přirozeně, pro usnadnění vyjádření polohy objektu vzhledem k nulovým souřadnicím v systému se předpokládají kladné a záporné hodnoty. Dnes však najdete další systémy.

Odrůdy souřadnicových systémů

Jak již bylo uvedeno, obdélníkový souřadný systém, který vytvořil Descartes, je dnes hlavní. Nicméně v některých technikách pro definování umístění objektu v trojrozměrném prostoru se používají jiné odrůdy.

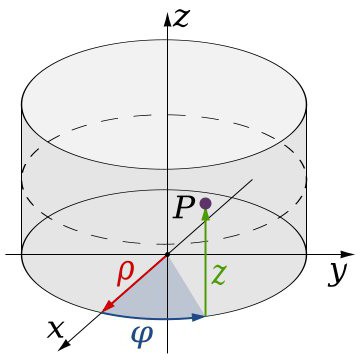
Nejznámější jsou válcovité a sférické systémy. Rozdíl od klasické je, že při zadání stejných tří hodnot, které určují umístění bodu v trojrozměrném prostoru, je jedna z hodnot úhlová. Jinými slovy, v takových systémech se používá kružnice odpovídající úhlu 360 stupňů. Odtud a specifický úkol souřadnic, včetně prvků jako poloměr, úhel a generátor. Souřadnice v trojrozměrném prostoru (systému) tohoto typu se řídí poněkud odlišnými zákony. Jejich úloha v tomto případě je řízena pravidlem pravé ruky: pokud kombinujete palec a ukazováček s osami X a Y, zbývající prsty v ohnuté poloze naznačují směr osy Z.

Koncept linie v trojrozměrném prostoru

Nyní pár slov o tom, co představuje přímku v trojrozměrném prostoru. Na základě základní koncepce přímky se jedná o nekonečnou řadu vykreslenou bodem nebo dvěma, bez počítání množiny bodů umístěných v posloupnosti, které nemění přímý průchod čarou mezi nimi.

Pokud se podíváte na čáru vykreslenou přes dva body v trojrozměrném prostoru, budete muset vzít v úvahu tři souřadnice obou bodů. Totéž platí pro segmenty a vektory. Ty druhé určují základ trojrozměrného prostoru a jeho rozměru.

Definice vektorů a základ trojrozměrného prostoru

Jak se běžně domníváme, v trojrozměrném souřadnicovém systému mohou být tři hlavní vektory, které definují základ. Navíc základny s odpovídajícími nezávislými třemi vektory mohou být bezpočet.

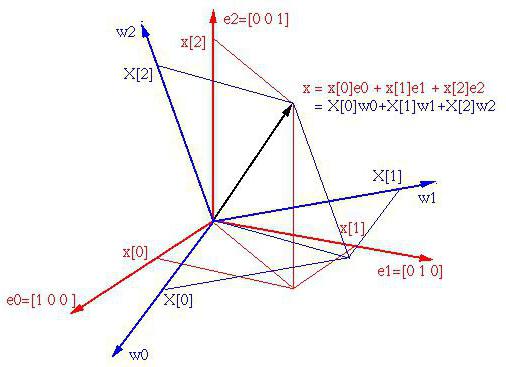
Všimněte si, že mohou existovat pouze tři vektory, ale zde můžete definovat až trojnásobek vektorů. Rozměr prostoru je určen počtem lineárně nezávislých vektorů (v našem případě tři). A prostor, ve kterém je konečný počet takových vektorů, se nazývá konečný rozměr.

Závislé a nezávislé vektory

Pokud jde o definici závislých a nezávislých vektorů, vektory, které jsou projekcemi (například vektory osy X promítané na ose Y), jsou považovány za lineárně nezávislé.

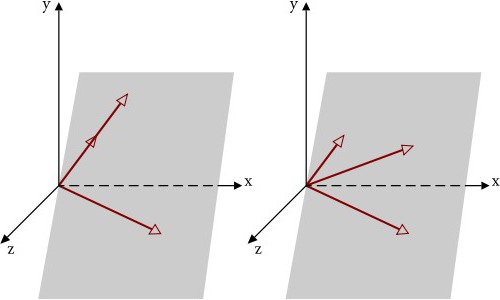
Jak je již zřejmé, je každý čtvrtý vektor závislý (teorie lineárních prostorů). Ale tři nezávislé vektory v trojrozměrném prostoru by neměly nutně ležet ve stejné rovině. Kromě toho, pokud definujeme nezávislé vektory v trojrozměrném prostoru, nemohou být, tak řečeno, jedno pokračování druhého. Jak je již zřejmé, v případě, že uvažujeme s třemi dimenzemi, podle obecné teorie lze sestavit pouze tři trojnásobek lineárně nezávislých vektorů v určitém souřadném systému (bez ohledu na typ).

Rovina v trojrozměrném prostoru

Pokud zvážíme koncept letadla, aniž bychom se dostali do matematických definic, pro jednodušší porozumění tohoto pojmu může být takový objekt považován pouze za dvourozměrný. Jinými slovy je to nekonečná sbírka bodů, kde jedna z souřadnic je konstantní (konstantní).

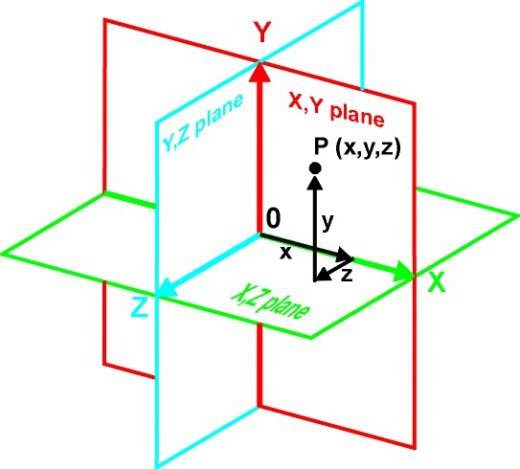
Například rovina může být nazvána libovolným počtem bodů s různými souřadnicemi podél os X a Y, ale se stejnými souřadnicemi podél osy Z. V každém případě zůstane jedna z trojrozměrných souřadnic nezměněna. Nicméně to je, tak říkají, obecný případ. V některých situacích se trojrozměrný prostor může protínají rovinou po všech osách.

Existují více než tři rozměry

Otázka, kolik měření může existovat, je docela zajímavé. Předpokládáme, že v klasickém pohledu na prostor, ale ve čtyřrozměrném, nežijeme v trojrozměrném. Vedle dobře známých délek, šířky a výšky zahrnuje tento prostor také životnost objektu a čas a prostor jsou velmi propojeny. Toto dokázal Einstein v jeho teorii relativity, i když se to týká víc fyzik, než algebry a geometrie.

Další zajímavostí je, že dnes vědci již prokázali existenci nejméně dvanácti dimenzí. Samozřejmě, daleko od všech bude schopen porozumět tomu, co jsou, protože se odkazuje spíše na určitou abstraktní oblast, která je mimo lidské vnímání světa. Nicméně fakt zůstává. A to není nic, co mnoho antropologů a historiků tvrdí, že naši předkové mohou mít nějaké specificky vyvinuté smyslové orgány, jako je třetí oko, které pomohly vnímat vícerozměrnou realitu a nikoliv pouze trojrozměrný prostor.

Mimochodem, dnes je spousta názorů na skutečnost, že extrasenzorické vnímání je také jedním z projevů vnímání vícerozměrného světa a lze najít spoustu důkazů.

Všimněte si, že moderní základní rovnice a věty popisují multidimenzionální prostory, které se liší od našeho čtyřrozměrného světa, není také možné vždy. A věda v této oblasti se více vztahuje k oblasti teorií a předpokladů, než k tomu, co může být jasně cítit, nebo tak řečeno, dotčeno nebo viděno z první ruky. Nicméně, nepřímý důkaz o existenci vícerozměrných světů, ve kterých mohou existovat čtyři nebo více dimenzí, je dnes bezpochyby.

Závěr

Obecně jsme velmi stručně přehodnotili základní pojmy týkající se trojrozměrného prostoru a základních definic. Samozřejmě existuje mnoho zvláštních případů spojených s různými souřadnicovými systémy. Navíc jsme se snažili dostat se do divočiny matematiky, abychom vysvětlili základní pojmy, pouze proto, aby byla otázka, která je s nimi spojena, srozumitelná jakémukoli školnímu dítěti (tak je to vysvětlení "na prstech").

Nicméně se zdá, že i z takových jednoduchých interpretací lze vyvodit závěr, že matematický aspekt všech složek zahrnutých do základního školního kurzu algebry a geometrie.