Jaký je moment setrvačnosti: vzorce pro tyč a kolo

Jakýkoli pohyb těles ve vesmíru, jehož trajektorií je kruh, znamená znát nejen úhlovou rychlost, ale i moment setrvačnosti pro popis tohoto pohybu. Jaký je okamžik setrvačnosti, stejně jako to, co je stejné pro prut a kolo, tento článek bude odpovídat.

Rotace a moment setrvačnosti

Fyzikální veličina, která se nazývá moment setrvačnosti, je zpravidla označována písmenem I a objevuje se ve fyzice při zvažování momentu hybnosti materiálu, který se otáčí kolem osy. Uhlový moment L ve skalární podobě je napsán následujícím výrazem:

L = r * m * v

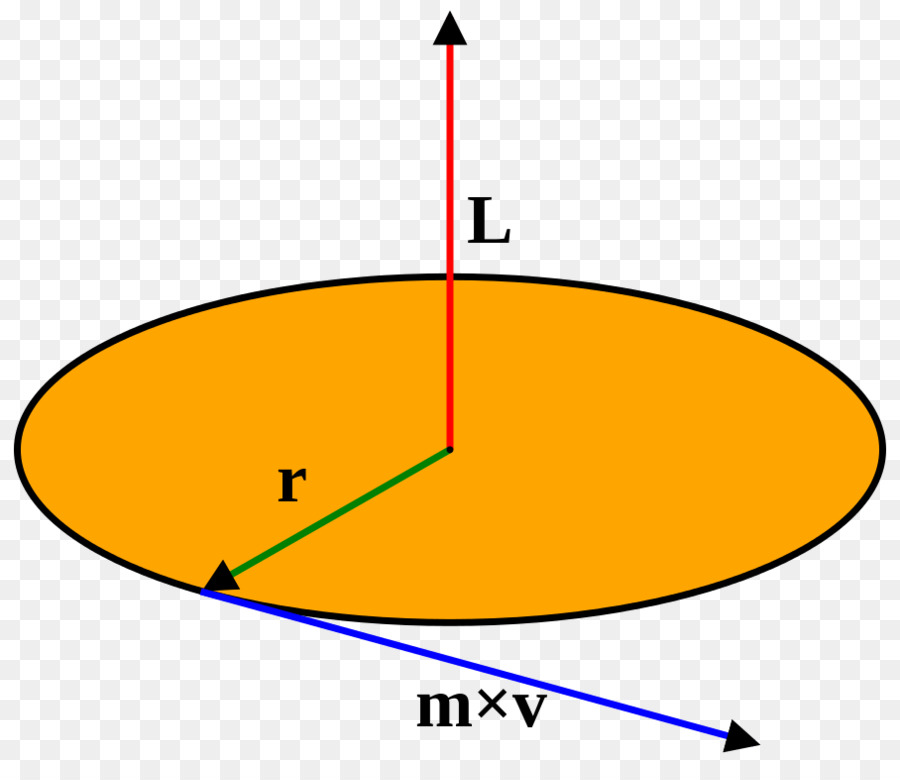
Zde r je vzdálenost k ose bodu materiálu, m je jeho hmotnost, v je lineární rychlost. Použitím vztahu posledně uvedeného s úhlovou rychlostí ω, získáme výraz:

L = r2 * m * ω, kde ω = v / r

Při odpovědi na otázku, co je moment setrvačnosti, je třeba říci, že toto je hodnota I = r ² * m. To znamená, že záleží na hmotnosti rotujícího objektu, roste s rostoucí vzdáleností k ose a měří se v kg * m ² .

Obecný výraz pro okamžik setrvačnosti

Vzorec zavedený v předchozím odstavci pro hodnotu I je platný, pokud jsou rozměry objektu zanedbatelné ve srovnání s vzdáleností k ose r (Země se otáčí kolem naší hvězdy). Pokud se lineární rozměry objektu stanou srovnatelné se vzdáleností r, pak je nutné vypočítat I pro použití obecnějšího vzorce, které je uvedeno níže:

I = ∫ _m (r ² * dm)

Ukazuje, že integrantem je okamžik setrvačnosti hmotného bodu. Součet všech okamžiků z bodů s hmotností dm je celkový moment setrvačnosti I pro celé tělo.

Tento vzorec je silným nástrojem pro určení těla I absolutně jakéhokoli tvaru. Podle vzorce je hodnota I aditive, to znamená, že umožňuje rozdělit tělo na jednotlivé části, vypočítat momenty setrvačnosti a poté přidat výsledky k získání hodnoty těla I.

Fyzický význam I

Vědět, jaký moment setrvačnosti je, je třeba říci pár slov o tom, jak jeho hodnota ovlivňuje chování a vlastnosti rotace skutečných objektů.

Velká hodnota I vede k tomu, že tělo je velmi obtížné otáčet kolem osy. K tomu musíte vykonat významnou práci a vynaložit značné úsilí. Příkladem těla s velkým I je zotrvačník automobilu - těžký kovový kotouč pevně namontovaný na klikovém hřídeli motoru. Naopak, pokud je hodnota systému I malá, pak může být rychle odpojena a stejně rychle a snadno zastavena. Příkladem toho je hliníkový okraj kola kola.

Výše uvedená diskuse naznačuje, že moment setrvačnosti je charakterizován setrvačností procesu rotace, to znamená, že plní stejnou roli jako hmotnost těla při působení síly, aby se dosáhlo zrychlení.

Rozdíl mezi hmotností a okamžikem setrvačnosti spočívá nejen v měřicích jednotkách, ale také ve skutečnosti, že druhá je funkcí rotačního systému a nejen geometrie těla a jeho hmoty.

Moment setrvačnosti kolem osy otáčení protínající střed hmoty tyče

Zvažte příklad použití integrálního vzorce pro řešení skutečných problémů. Nejdříve řešíme jednoduchý problém: existuje tenká tyč o délce l a hmotnosti m. Osa se otáčí kolmo k této tyči středem hmoty objektu. Je nutné určit hodnotu I pro tento systém.

Napíšeme obecný vzorec pro setrvačnost momentu tyče o ose, máme:

I = ∫ _m (r ² * dm)

Vzhledem k tomu, že osa je kolmá na dotyčné těleso a samotná tyč má nekonečně malou tloušťku, je možné ji mentálně vystřihnout do tenkých vrstev rovinami rovnoběžnými s osou. V tomto případě zjistíme, že prvek hmotné dm může být reprezentován následující rovnicí:

dm = ρ * s * dr

Zde ρ je hustota materiálu, S je průřez, který je konstantní a má tendenci k nule (tyč je nekonečně tenká). Nahraďte tento výraz obecným vzorem:

I = ρ * S * ∫ ^{+ l / 2-} _{l / 2} (r ² * dr)

Všimněte si, že substituované integrační limity pro r odpovídají stavu problému (osa rozděluje tyč na dvě stejné části). Při provádění integrace získáváme:

I = ρ * S * (r 3/3) ^{+ l / 2-} _{l / 2} = m * l 2/12, kde m = ρ * S * 1

Tedy moment setrvačnosti tenké tyče, když os prochází středem hmoty, je 12krát menší než moment hmotného bodu stejné hmotnosti umístěný ve vzdálenosti l od osy.

Hodnota I pro tyč s osou otáčení na konci objektu

Zvažte, co je moment setrvačnosti, v poněkud odlišné situaci. Máme tentýž předmět (tenká tyč), ale nyní os prochází koncem. Jak se v tomto případě změní okamžik setrvačnosti? Při použití stejného způsobu rozdělení tyče a následné integrace, jako v předchozím odstavci, získáváme:

I = ρ * S * ∫ ^l ₀ (r ² * dr)

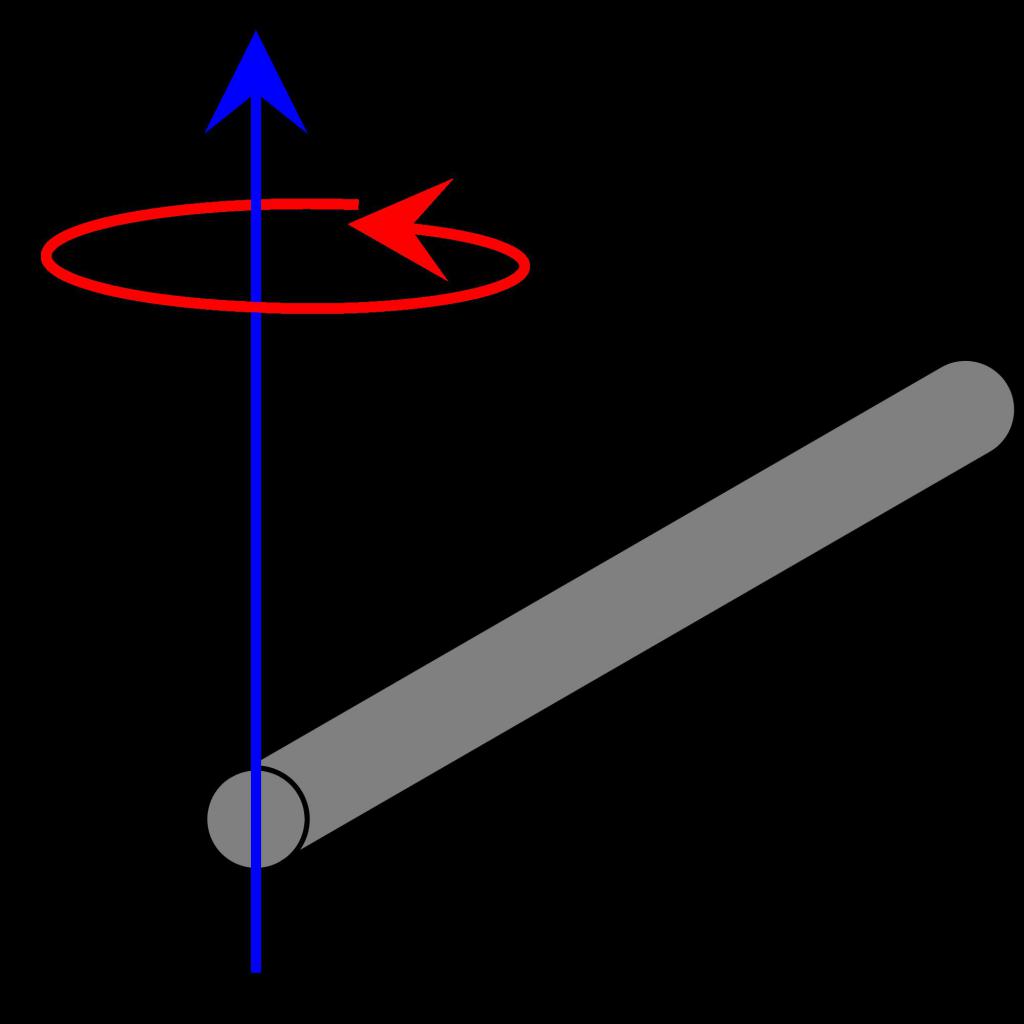
Všimněte si, že se změnily pouze limity integrace. Řešením je následující rovnost:

I = m * l 2/3

Výraz ukazuje, že stejná tyč bude mít čtyřnásobek velkého momentu setrvačnosti (obtížnějšího otáčení), pokud se osa otáčení posouvá od středu k okraji.

Vzhledem k řešení těchto dvou problémů je nutno učinit důležitý závěr: při výpočtu hodnoty I je nemožné snížit celkovou hmotnost předmětu do jeho středu a provést výpočet jako materiálový bod. Výpočet by měl být prováděn pouze za použití integrálního výrazu.

Myslím si, že jsem spokojen

Moment setrvačnosti kola lze stanovit pomocí vlastnosti aditivity uvažovaného množství. Chcete-li to provést, duševně rozložte kolo na samostatné části, které představují paprsky a okraj. Jelikož je jehla tenká a její osa otáčení prochází koncem, platí pro ni vzorec získaný v předchozím odstavci.

Pokud jde o ráfek kola, jeho moment setrvačnosti je podobný momentu setrvačnosti, který se pohybuje v bodě materiálu umístěném ve vzdálenosti poloměru kola a má hmotnost ráfku.

Přidáním momentů setrvačnosti všech elementů získáme:

I = n * m _c * r 2/3 + m _o * r ²

Zde _mc a m _o jsou spisy a okrajové masky, n je počet paprsků. Pokud všechny paprsky váží mnohem méně než ráfek, potom setrvačnost kol bude rovna:

I = m _o * r ² pokud n * m _c < o

Znalost hodnoty I pro kolo je důležitá při výpočtu úhlové rychlosti a momentu otáčení koleček jakéhokoliv vozidla (auto, jízdní kolo).