Úhel úhlu v geometrii

V tomto článku budeme zvažovat jeden z hlavních geometrických tvarů - úhel. Po obecném úvodu k této koncepci se zaměříme na konkrétní typ takového čísla. Rozvinutý úhel je důležitou koncepcí geometrie, která bude hlavním tématem tohoto článku.

Úvod do konceptu geometrického úhlu

V geometrii existuje řada objektů, které tvoří základ všech věd. Úhel, jenž je zachází a je určen pomocí konceptu paprsku, a tak začneme s ním.

Také předtím, než začnete určit vlastní úhel, musíte vzpomenout na několik stejně důležitých objektů v geometrii - to je bod, přímo v rovině a rovině samotné. Rovná čára se nazývá nejjednodušší geometrická postava, která nemá žádný začátek ani konec. Rovina je povrch, který má dva rozměry. No, paprsek (nebo semi-přímý) v geometrii je čára přímky, která má počátek, ale žádný konec.

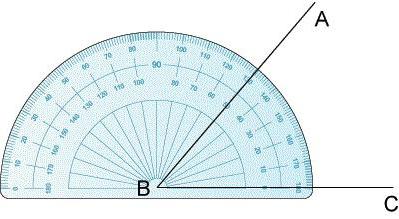
Pomocí těchto konceptů můžeme konstatovat, že úhel je geometrický obraz, který leží zcela v určité rovině a sestává ze dvou nesouvislých paprsků se společným počátkem. Takové paprsky se nazývají strany úhlu a společný původ stran je jeho vrchol.

Typy úhlů a geometrie

Víme, že úhly mohou být zcela jiné. A protože trochu nižší bude dána malá klasifikace, která pomůže lépe pochopit typy úhlů a jejich hlavní rysy. Existuje tedy několik typů úhlů v geometrii:

1. Pravý úhel Je charakterizována velikostí 90 stupňů, což znamená, že jeho strany jsou vždy vzájemně kolmé.
2. Ostrý úhel. Tyto rohy zahrnují všechny jejich zástupce, jejichž velikost je menší než 90 stupňů.
3. Špinavý roh. Zde můžete mít všechny úhly od 90 do 180 stupňů.
4. Úhel Má velikost přesně 180 stupňů a směrem ven je jedna rovná.

Koncept rozvinutého úhlu

Nyní se podívejme podrobněji na rozšířený úhel. To je případ, kdy obě strany leží na jedné přímce, což je zřetelně vidět na obrázku o něco nižší. To znamená, že můžeme s jistotou říci, že jedna ze stran jeho rozvinutého úhlu je v podstatě pokračováním druhého.

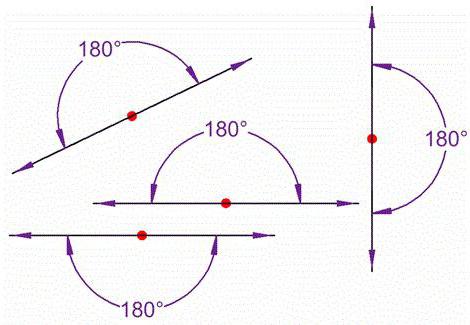
Stojí za zmínku skutečnost, že takový úhel lze vždy rozdělit pomocí nosníku, který vychází z jeho vrcholu. Jako výsledek získáváme dva úhly, které se v geometrii nazývají přilehlé.

Také rozvinutý roh má několik funkcí. Abyste mluvili o prvním z nich, musíte si vzpomenout na koncept "bisector of the corner". Připomeňme, že se jedná o paprsek, který dělí jakýkoli úhel přísně na polovinu. Co se týče rozloženého úhlu, dělí se jeho poloha tak, že se vytvoří dva pravé úhly o 90 stupňů. Je velmi snadné vypočítat matematicky: 180˚ (stupeň rozloženého úhlu): 2 = 90˚.

Rozdělíme-li rozložený úhel absolutně libovolným paprskem, pak v důsledku toho vždy získáme dva úhly, z nichž jeden bude ostrý a druhý - tupý.

Vlastnosti rozšířených rohů

Bude vhodné zvažovat tento úhel, který spojuje všechny jeho hlavní vlastnosti, které jsme udělali v tomto seznamu:

1. Boky rozloženého úhlu jsou protiparalelní a jsou rovné.
2. Velikost rozloženého úhlu je vždy 180 °.
3. Dva sousední rohy dohromady vždy tvoří rozložený úhel.
4. Celý úhel, který je 360 ​​°, se skládá ze dvou nasazení a je roven jejich součtu.
5. Poloviční rozložený úhel je pravý úhel.

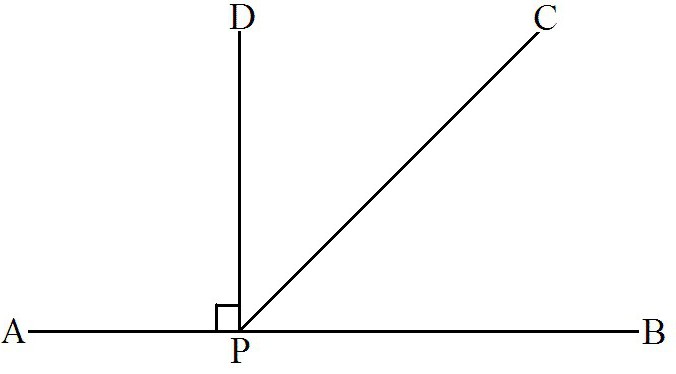
Takže, když známe všechny tyto charakteristiky tohoto typu úhlů, můžeme je použít k vyřešení řady geometrických problémů.

Úkoly s rozšířenými rohy

Abyste pochopili, zda jste porozuměli konceptu vyvinutého úhlu, pokuste se odpovědět na několik následujících otázek.

1. Jaký je rozložený úhel, pokud jeho strany vytvářejí svislou čáru?
2. Budou dva rohy sousední, pokud velikost první rohy je 72˚ a druhá je 118˚?
3. Je-li plný úhel tvořen dvěma rozvinutými, kolik je v něm pravý úhel?
4. Rozšířený úhel byl dělen paprskem do dvou takových úhlů, že jejich míra se vztahuje na 1: 4. Vypočtěte získané úhly.

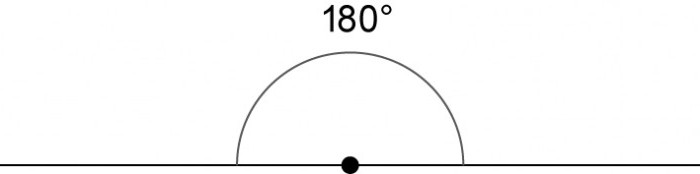
Řešení a odpovědi:

1. Bez ohledu na to, jak je rozložený úhel umístěn, je vždy podle definice 180.
2. Sousední úhly mají jednu společnou stranu. Proto pro výpočet velikosti úhlu, který tvoří dohromady, stačí přidat hodnotu jejich míry. Takže, 72 +118 = 190. Ale podle definice je rozložený úhel 180 °, což znamená, že tyto dva úhly nemohou být sousední.
3. Rozvinutý úhel má dva pravé úhly. A jelikož jsou dva zcela nasazené, znamená to, že v něm budou čtyři přímky.
4. Pokud nazýváme požadované úhly a a b, pak nechť x je koeficient proporcionality pro ně, což znamená, že a = x, a tedy b = 4x. Rozšířený úhel ve stupních je 180 °. A podle jeho vlastností je míra úhlu vždy stejná jako součet stupňových měřítek úhlů, do kterých je dělen nějakým libovolným paprskem, který prochází mezi jeho stranami, a můžeme usoudit, že x + 4x = 180˚ a tedy 5x = 180˚ . Odtud nalezneme: x = a = 36˚ a b = 4х = 144˚. Odpověď je 36˚ a 144˚.

Pokud se vám podařilo odpovědět na všechny tyto otázky bez výzvy a nehleděte-li se na odpovědi, jste připraveni pokračovat v další geometrické výuce.