Blokový diagram: příklady, prvky, konstrukce. Vývojové diagramy

Tento článek se bude zabývat příklady vývojových diagramů, se kterými se můžete setkat v učebnicích o počítačové vědě a jiné literatuře. Vývojový diagram je algoritmus, který řeší jakýkoli úkol, který je určen vývojáři. Nejprve musíte odpovědět na otázku, co je algoritmus, jak je graficky znázorněn a co je nejdůležitější, jak ho vyřešit, znát určité parametry. Mělo by být ihned poznamenáno, že existuje několik druhů algoritmů.

Co je to algoritmus?

Toto slovo uvedlo do provozu matematik Mohammed al-Khorezmi, který žil v období 763-850 let. Právě on je ten, kdo vytvořil pravidla pro provádění aritmetických operací (tam jsou jen čtyři). Ale GOST z roku 1974, který uvádí, že:

Algoritmus je přesný předpis, který definuje výpočetní proces. Kromě toho existuje několik proměnných s uvedenými hodnotami, které vedou k výpočtu požadovaného výsledku.

Algoritmus umožňuje jasně určit výkonného subjektu tak, aby byl přísný sled akcí vyřešit problém a získat výsledek. Vývoj algoritmu je rozdělení jednoho velkého úkolu do určité posloupnosti kroků. Kromě toho musí vývojář algoritmu znát všechny funkce a pravidla pro jeho vytvoření.

Funkce algoritmu

Celkem je osm funkcí algoritmu (bez ohledu na jeho typ):

1. K zadání počátečních dat je funkce.
2. Po dokončení algoritmu je závěr určitého výsledku. Je třeba si uvědomit, že algoritmus je potřebný k dosažení určitého cíle, totiž k získání výsledku, který přímo souvisí se zdrojovými daty.
3. Tento algoritmus musí mít strukturu s diskrétním typem. Měl by být prezentován v postupných krocích. Navíc každý další krok může začít až po dokončení předchozího kroku.
4. Tento algoritmus musí být jednoznačný. Každý krok je jasně definován a neumožňuje libovolnou interpretaci.
5. Algoritmus musí být konečný - je nutné, aby byl proveden v přesně definovaném počtu kroků.
6. Algoritmus musí být správný - požádat o správné řešení problému.
7. Komunita (nebo hromadný znak) - měla by pracovat s různými zdrojovými daty.
8. Doba daná řešením algoritmu by měla být minimální. To určuje účinnost úkolu.

A nyní, když víte, jaké algoritmové vývojové diagramy existují, můžete začít zvážit, jak je napsat. A nejsou příliš mnoho.

Slovní záznam

Tento formulář se obvykle používá při popisu postupu pro osobu: "Jdi tam, nevím kde. Přineste něco, nevím co. "

Samozřejmě je to komická forma, ale podstata je jasná. Příkladem je například obvyklý záznam na oknech autobusů: "V případě nehody vytáhněte kabel, vytlačte sklo".

Zde je jasně stanovena podmínka, podle které musí být dvě akce provedena v přísném pořadí. Ale to jsou nejjednodušší algoritmy, jsou složitější. Někdy se používají vzorce, speciální označení, ale s povinnou podmínkou - umělec musí pochopit všechno.

Je povoleno změnit pořadí akcí, jestliže je třeba vrátit se například k předchozí operaci nebo obejít nějaký příkaz za určitých podmínek. Současně je žádoucí počítat týmy a uvést povel, ke kterému se přechod uskutečňuje: "Po dokončení všech manipulací opakujte body 3 až 5".

Nahrajte v grafické podobě

Tento záznam obsahuje prvky vývojových diagramů. Všechny prvky jsou standardizovány, každý tým má určitý grafický záznam. Zvláštní příkaz musí být zaznamenán v každém z bloků v běžném jazyce nebo matematickém vzorci. Všechny bloky musí být připojeny čarami - ukazují přesně to, jaký pořadí mají vykonané příkazy. Tento typ algoritmu je vhodnější spíše pro použití v programovém kódu než verbálním.

Psaní v programovacích jazycích

V takovém případě, pokud je algoritmus potřebný k tomu, aby úkol mohl být vyřešen programem nainstalovaným v počítači, musíte jej zapsat speciálním kódem. K tomu je mnoho programovacích jazyků. A algoritmus v tomto případě se nazývá program.

Vývojové diagramy

Blokový diagram je reprezentací algoritmu v grafické podobě. Všechny týmy a akce jsou reprezentovány geometrickými tvary (bloky). Uvnitř každého obrázku odpovídají všechny informace o akcích, které je třeba provést. Připojení jsou zobrazena jako normální čáry se šipkami (v případě potřeby).

Pro návrh diagramů algoritmů existuje GOST 19.701-90. Popisuje postup a pravidla pro jejich vytváření v grafické podobě, stejně jako základní metody řešení. Tento článek představuje hlavní prvky vývojových diagramů, které se používají při řešení problémů, například v oblasti výpočetní techniky. A teď se podíváme na pravidla výstavby.

Základní pravidla pro vytváření vývojového diagramu

Existují takové funkce, které by měl mít vývojový diagram:

1. Musí být přítomny dva bloky - "Start" a "End". A v jediné kopii.
2. Od počátečního bloku k konečnému odkazu by mělo být vykresleno.
3. Ze všech bloků, s výjimkou posledního, by měly proudové vedení vycházet.
4. Musí existovat číslování všech bloků: shora dolů, zleva doprava. Pořadové číslo by mělo být umístěno v levém horním rohu, což by znamenalo zlomení značky.
5. Všechny bloky musí být vzájemně propojeny řadami. Musejí určit sekvenci, s jakou se provádějí akce. Pokud se průtok pohybuje nahoru nebo zprava doleva (jinými slovy, v opačném pořadí), pak se nakreslí šipky.
6. Linky jsou rozděleny na odchozí a příchozí. Je třeba poznamenat, že jeden řádek je pro jeden blok odchozí a pro druhý příchozí.
7. Z počátečního bloku v schématu tok linky opouští, protože to je první.
8. Ale poslední blok má pouze vstup. To je jasně ukázáno v příkladech vývojových diagramů, které jsou k dispozici v článku.
9. Pro snadnější čtení vývojových diagramů jsou příchozí linky vytaženy shora a odchozí linky zespodu.
10. Přítomnost mezer v tocích. Jsou nutně označeny speciálními konektory.
11. Pro usnadnění vývojového diagramu je dovoleno psát všechny informace v komentářích.

Grafické prvky vývojových diagramů pro řešení algoritmů jsou uvedeny v tabulce:

Algoritmy lineárního typu

Jedná se o nejjednodušší formulář, který se skládá ze specifické sekvence akcí, nezávisí na tom, jaké údaje jsou zadány zpočátku. Existuje několik příkazů, které jsou spuštěny jednou a až po dokončení předchozího příkazu. Lineární blokový diagram vypadá takto:

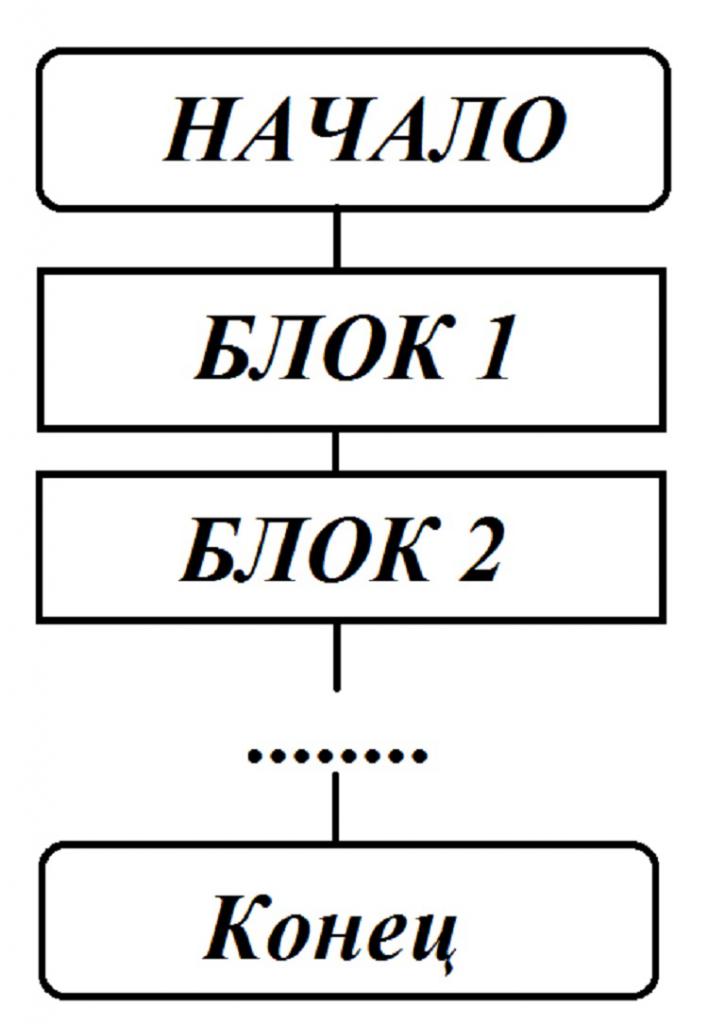
Odkazy navíc směřují shora dolů a zleva doprava. Takový vývojový diagram se používá k zápisu výpočtových algoritmů pomocí jednoduchých vzorců, které nemají žádné omezení hodnot hodnot proměnných obsažených ve vzorcích pro výpočet. Lineární algoritmus je nedílnou součástí komplexních výpočetních procesů.

Rozvětvovací algoritmy

Vývojové diagramy založené na takových algoritmech jsou složitější než lineární. Podstata se však nemění. Rozvětvovací algoritmus je proces, při němž další opatření závisí na tom, jak je podmínka splněna a jaké řešení je dosaženo. Každá linie akce je větev.

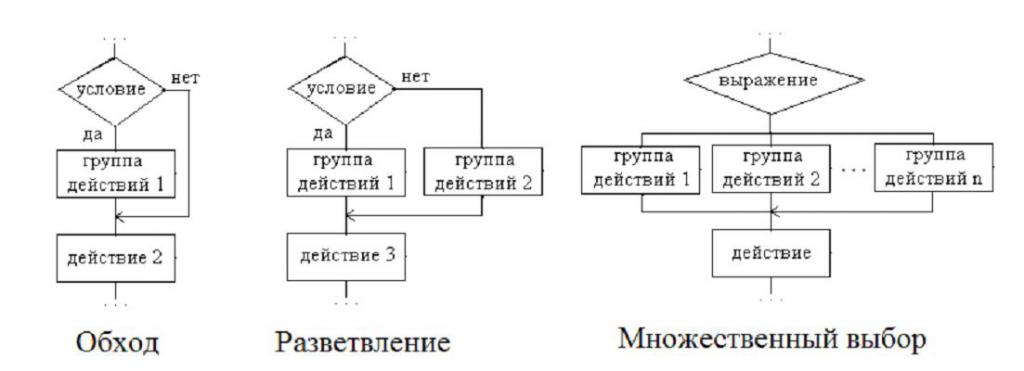
Grafy zobrazují bloky, které se nazývají "Řešení". Má dva východy a uvnitř je zapsán logický stav. Právě na tom, jak bude provedeno, závisí další pohyb v schématu algoritmu. Rozdělovací algoritmy můžete rozdělit do tří skupin:

1. "Bypass" - zatímco jedna z poboček nemá operátory. Jinými slovy, některé akce jiné pobočky jsou obcházeny.
2. "Branching" - každá pobočka má specifickou sadu provedených akcí.
3. "Vícenásobná volba" je vidlice, ve které je několik větví a každá obsahuje konkrétní soubor činností, které mají být provedeny. A je zde jedna funkce - volba směru přímo závisí na tom, jaké hodnoty jsou uvedeny pro výrazy obsažené v algoritmu.

Jedná se o jednoduché algoritmy, které jsou řešeny velmi jednoduše. Nyní se posunout k složitějším.

Cyklický algoritmus

Všechno zde je velmi jasné - cyklické blokové schéma představuje algoritmus, ve kterém se homogenní výpočty opakují mnohokrát. Podle definice je cyklus specifickou sekvencí všech akcí, které se provádějí vícenásobně (více než jednou). A existuje několik typů cyklů:

1. Kdo zná počet opakování akcí (nazývá se také cykly s počítadlem).
2. V nichž není počet opakování neznámý - s post-podmínkou a předpokladem.

Bez ohledu na to, jaký typ cyklu se používá k vyřešení algoritmu, musí mít proměnnou, s níž se výstup vyskytuje. Určuje počet opakování cyklu. Pracovní část (tělo) cyklu je specifická sekvence činností, která se provádí v každém kroku. A teď se budeme bližší podívat na všechny typy cyklů, které se mohou vyskytnout při přípravě algoritmů a řešení problémů s počítačem.

Počítačové cykly

Na obrázku je znázorněn jednoduchý blokový diagram, ve kterém je cyklus s počítadlem. Tento typ algoritmu ukazuje, že počet opakování daného cyklu je znám předem. A toto číslo je opraveno. V tomto případě se proměnná počítá počet kroků (opakování) nazývá počítadlo. Někdy se v učebnicích objevují další definice - parametr cyklu, řídicí proměnná.

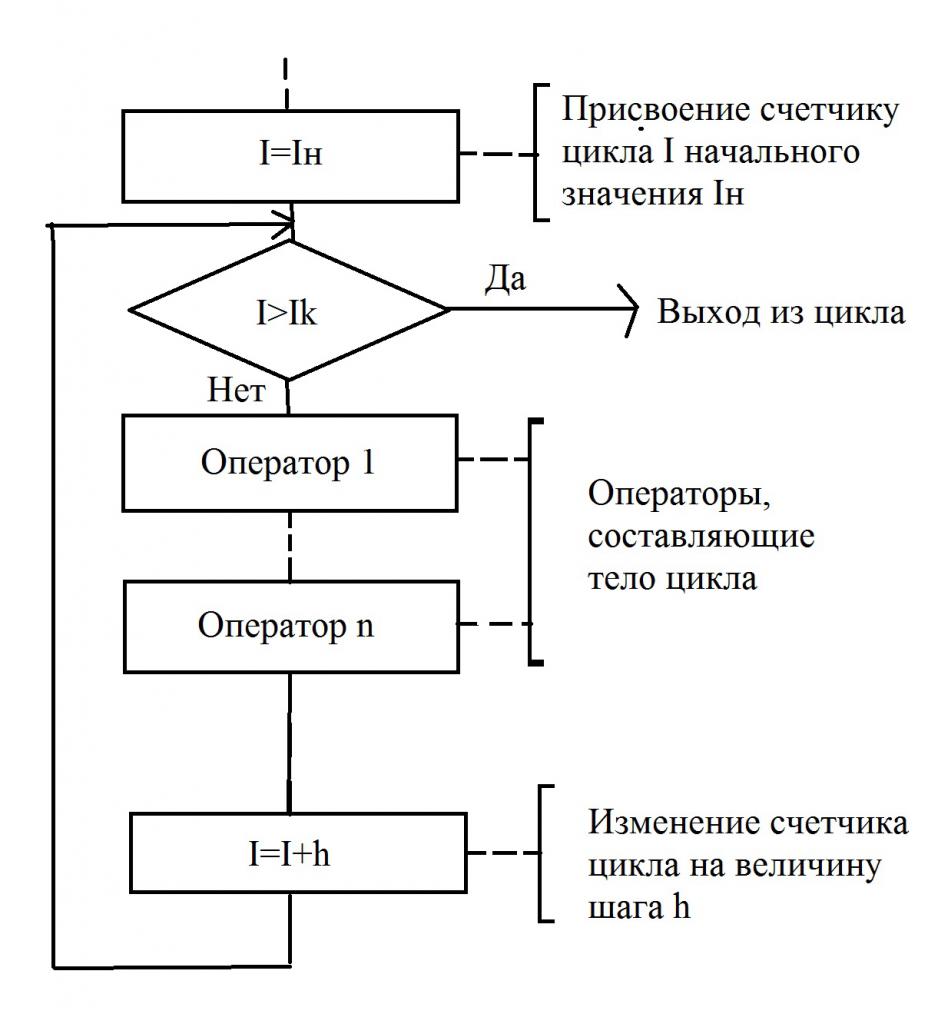
Bloková schéma velmi jasně ilustruje, jak smyčka funguje s počítadlem. Před provedením prvního kroku musíte přiřadit počáteční hodnotu počítadlu - může to být libovolné číslo, záleží na konkrétním algoritmu. V případě, že konečná hodnota je menší než hodnota počitadla, provede se určitá skupina příkazů, které tvoří tělo smyčky.

Po provedení těla se počítadlo změní o hodnotu přírůstku počitadla, označenou písmenem h. V případě, že získaná hodnota je menší než poslední, cyklus bude pokračovat. A bude končit pouze tehdy, když je konečná hodnota menší než počítadlo smyček. Pouze v tomto případě bude provedena akce, která následuje po cyklu.

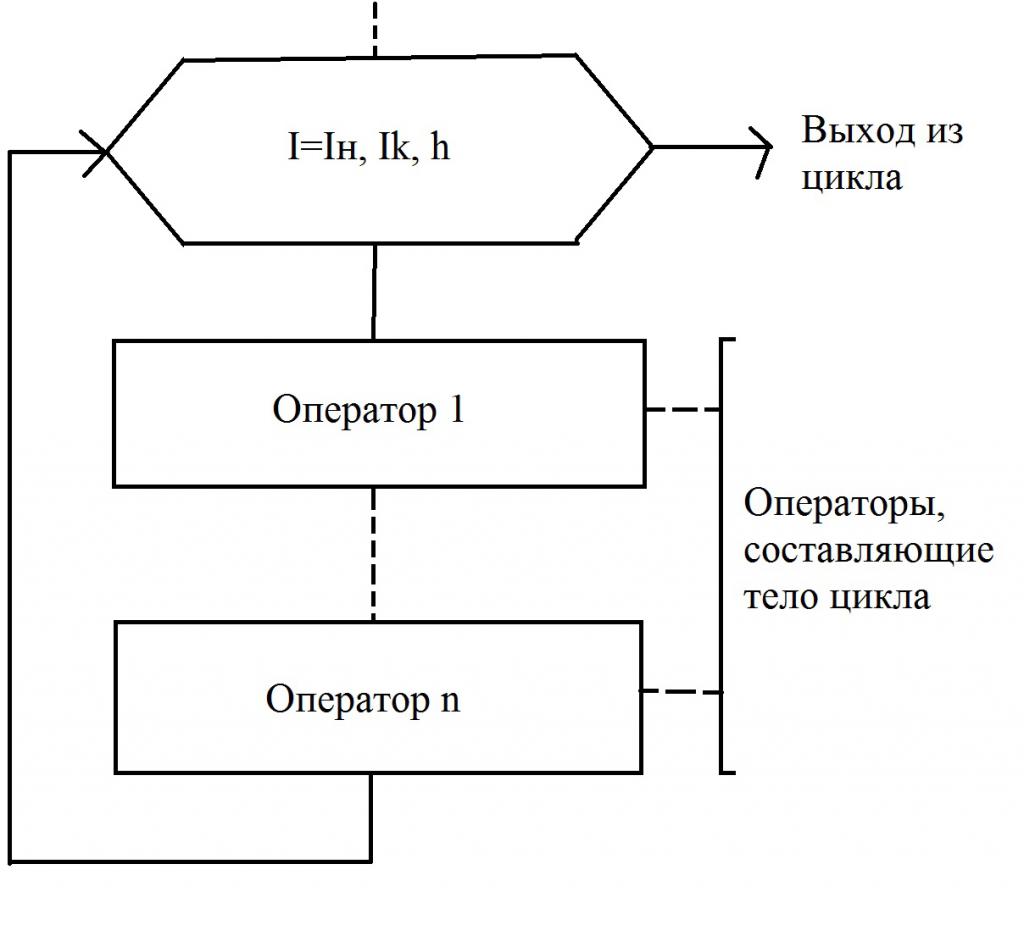
Typicky se v blokovém schématu používá blok nazvaný "Příprava". Je zapsána v počitadle a pak uveďte následující údaje: počáteční a konečné hodnoty, změna kroku. V blokovém schématu jsou to parametry I n, Ik a h. V případě, kdy h = 1, není velikost kroku zaznamenána. V ostatních případech je to nutné. Je nutné řídit se jednoduchým pravidlem - průtoková čára by měla vstupovat shora. A streamline, která jde dolů (nebo vpravo, v závislosti na konkrétním algoritmu), by měla ukazovat přechod k dalšímu operátorovi.

Nyní jste plně studovali popis vývojového diagramu, který je znázorněn na obrázku. Můžete pokračovat v dalším studiu. Při použití cyklu s počítadlem musí být splněny určité podmínky:

1. Tělo nesmí měnit (násilně) hodnotu počítadla.
2. Je zakázáno přenést ovládání zvenku na obsluhu těla. Jinými slovy, jeden může vstoupit do cyklu až od jeho začátku.

Předběžné cykly

Tento typ cyklů se používá v případech, kdy počet opakování není předem znám. Cyklus s předpokladem je druh algoritmu, ve kterém, bezprostředně předtím, než se tělo začne provádět, kontroluje stav, pod kterým je povolen přechod na další akci. Všimněte si, jak jsou zobrazeny prvky blokového diagramu.

V případě, že je podmínka splněna (výpis je pravdivý), nastane přechod na začátek těla cyklu. Přímo mění hodnotu alespoň jedné proměnné, která ovlivňuje hodnotu nastavené podmínky. Pokud se k tomuto pravidlu nedržíte, dostaneme "smyčku". V případě, že po dalším ověření stavu provedení těla smyčky se ukáže, že je nepravdivé, pak nastane výjezd.

Ve vývojových diagramech algoritmů je dovoleno kontrolovat ne pravdu, ale falešnost počátečního stavu. V tomto případě se cyklus ukončí, pouze pokud je hodnota podmínky splněna. Obě možnosti jsou správné, jejich použití závisí na tom, co konkrétně je vhodnější použít k vyřešení určitého problému. Tento typ cyklu má jednu funkci - tělo nemusí být spuštěno, pokud je podmínka falešná nebo pravdivá (v závislosti na variantě, která se používá k vyřešení algoritmu).

Níže je vývojový diagram, který popisuje všechny tyto akce:

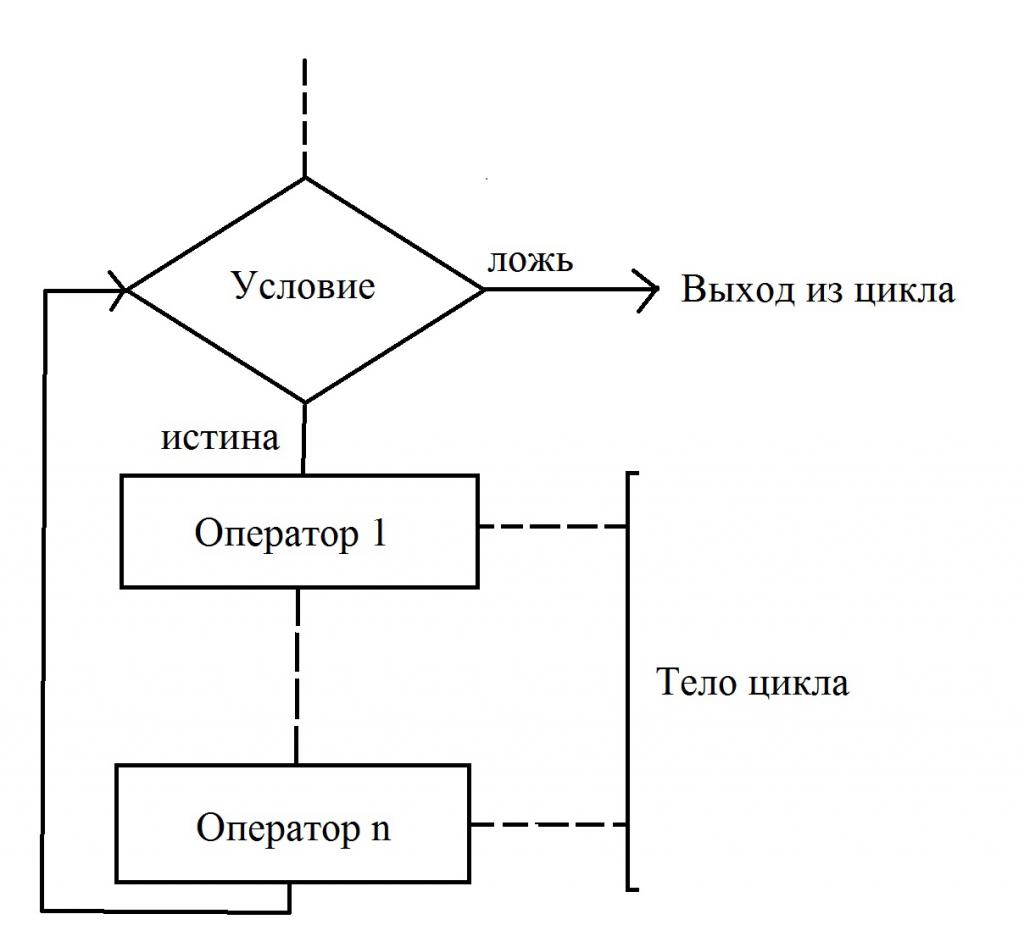
Co je cyklus s postcondition?

Pokud se podíváte pozorně, pak jsou tyto cykly poněkud podobné předchozímu cyklu. Budeme se snažit sestavit vývojový diagram popisující tento cyklus na vlastní pěst. Zvláštností je, že počet opakování není předem znám. A stav je stanoven po stažení z těla. To ukazuje, že tělo, bez ohledu na rozhodnutí, bude provedeno alespoň jednou. Pro přehlednost se podívejte na vývojový diagram, který popisuje podmínky a prohlášení:

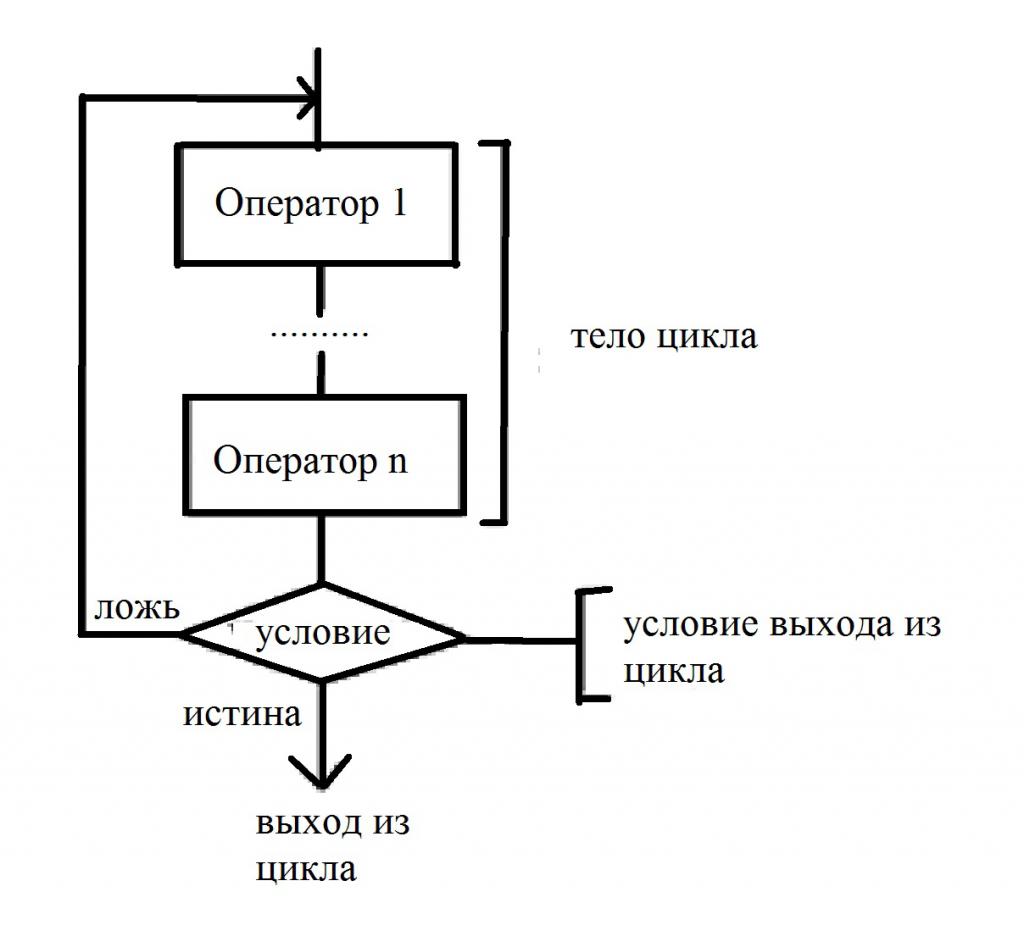
V konstrukci algoritmů s cykly není nic obtížného, ​​stačí je pochopit jen jednou. A nyní se obracíme ke složitějším strukturám.

Komplexní cykly

Komplexem jsou takové konstrukce, ve kterých je jeden nebo více jednoduchých cyklů. Někdy jsou nazývány vnořenými. Současně se ty struktury, které pokrývají jiné cykly, nazývají "vnější". A ty, které jsou součástí návrhu vnější - vnitřní. Když se provádí každý krok vnější smyčky, vnitřní smyčka se úplně posouvá, jak je znázorněno na obrázku:

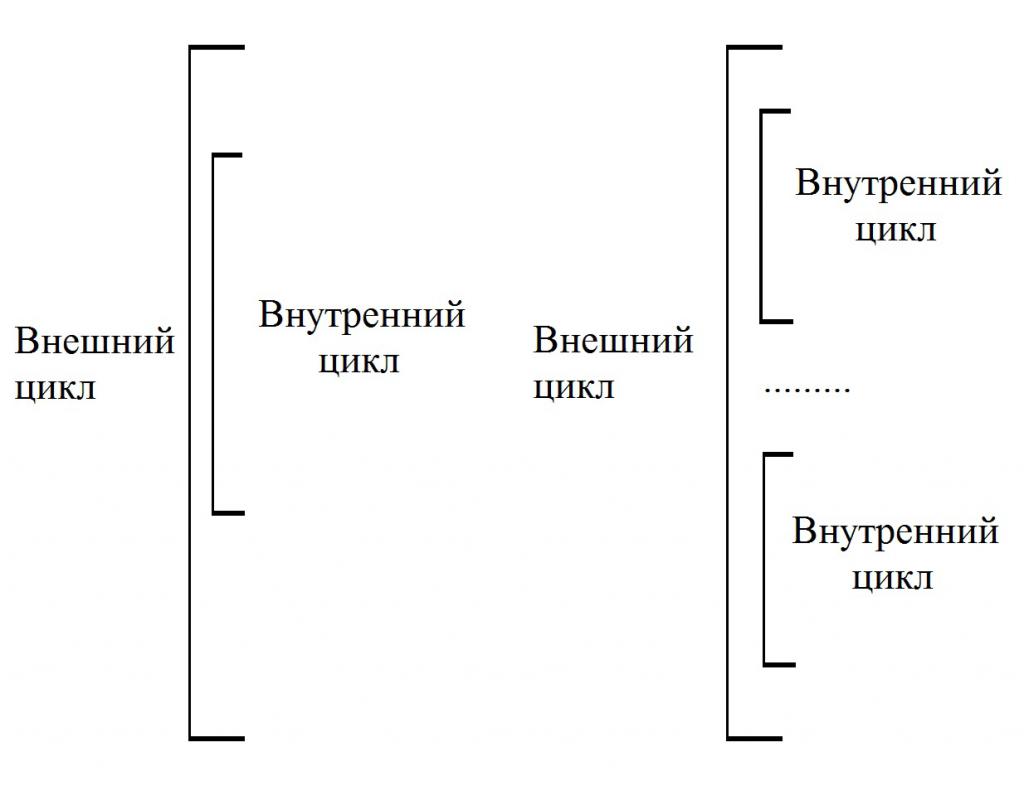
To je všechno, že jste přezkoumali hlavní rysy konstrukce vývojových diagramů pro řešení algoritmů, znáte zásady a pravidla. Nyní můžete uvažovat o konkrétních příkladech vývojových diagramů ze života. Například v psychologii se takové konstrukce používají, aby osoba mohla rozhodnout o otázce:

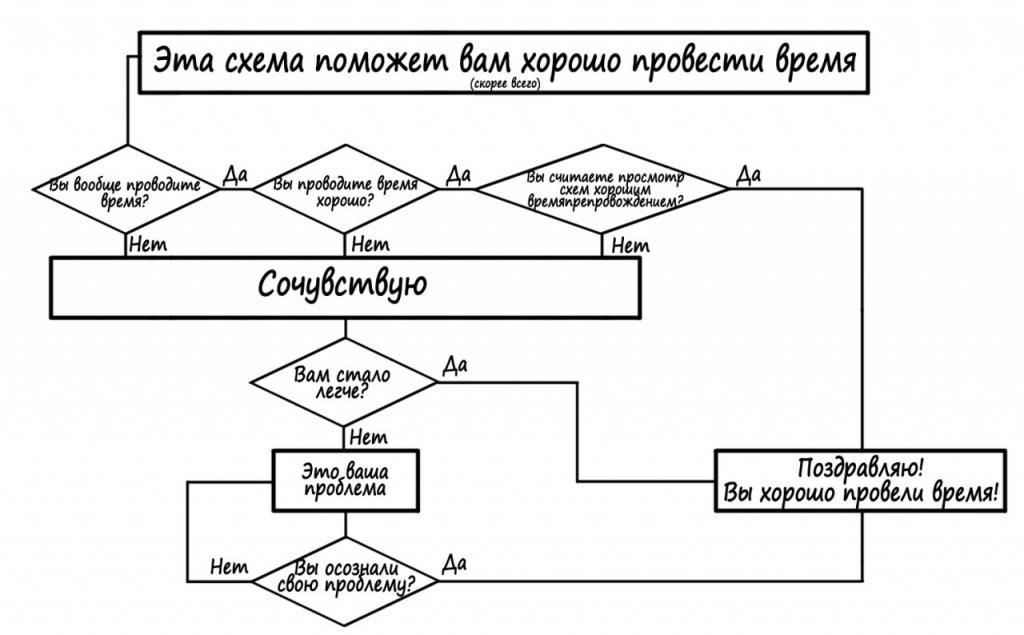
Nebo příklad z biologie k vyřešení problému:

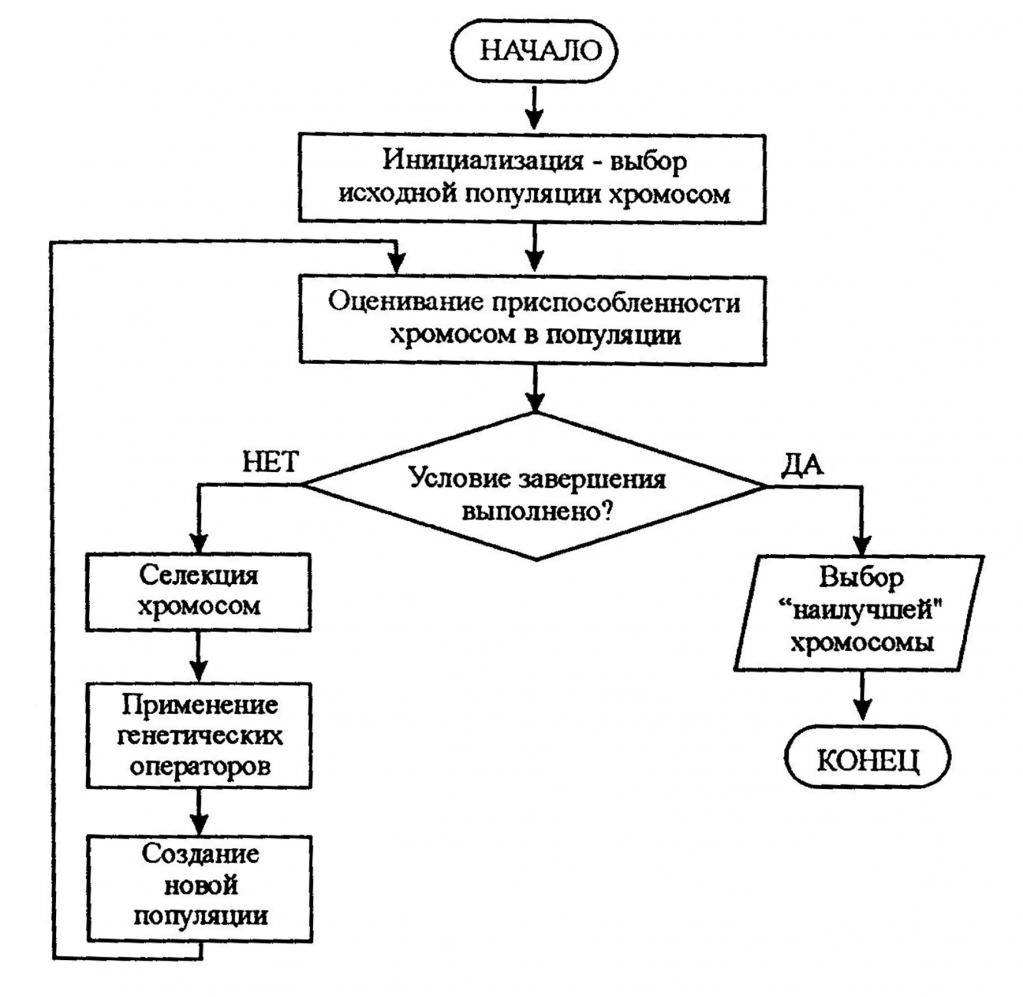
Řešení problémů s vývojovými diagramy

A teď se podíváme na příklady problémů s vývojovými diagramy, které lze nalézt v učebnicích počítačové vědy. Například je uveden blokový diagram, podle něhož je řešen nějaký algoritmus:

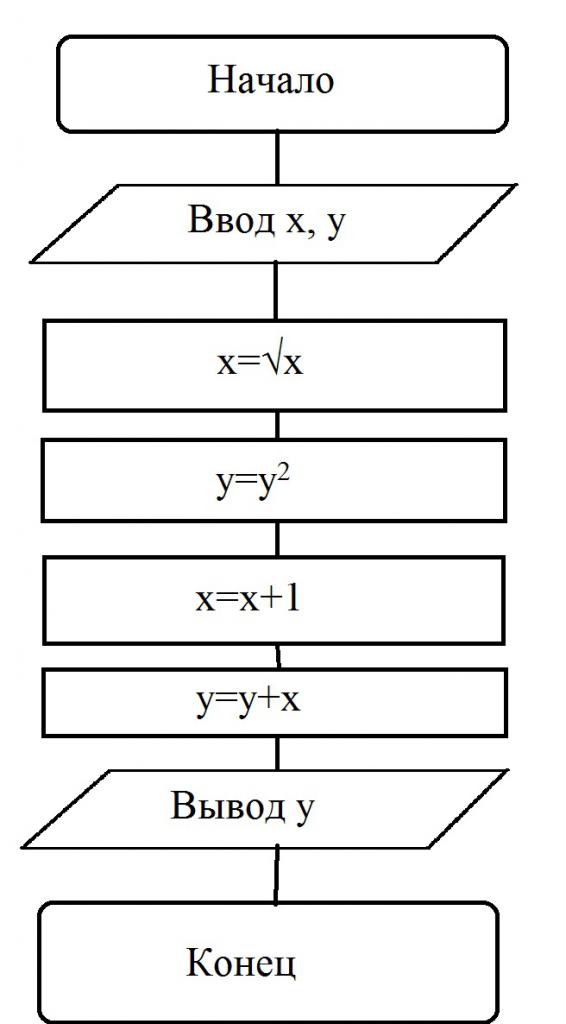
V tomto případě uživatel nezávisle zadává hodnoty proměnných. Předpokládejme, že x = 16 a y = 2. Proces tohoto postupu:

1. Zadávají se hodnoty x a y.
2. Provádí se konverze: x = √16 = 4.
3. Podmínka je splněna: y = y ² = 4.
4. Výpočet je proveden: x = (x + 1) = (4 + 1) = 5.
5. Další proměnná je vypočtena dále: y = (y + x) = (5 + 4) = 9.
6. Zobrazí se řešení: y = 9.

V tomto příkladu vývojové diagramy pro výpočetní techniky jasně ukazují, jak je algoritmus řešen. Musíte dbát na skutečnost, že hodnoty x a y jsou nastaveny v počáteční fázi a mohou být cokoliv.