Booleovský výraz: Vytvořte a zjednodušte

Hlavním úkolem logiky je zjistit, zda je výrok nepravdivý, nebo zda lze považovat za pravdivý. K tomu bylo vynalezeno několik metod. Vyvinuté způsoby, jak určit pravda je nebo nepravdivé, založené na jiných projevech a jejich atributech. Booleovský výraz - základna koncepce vědy a jeho parametry určují, které operace mohou být provedeny.

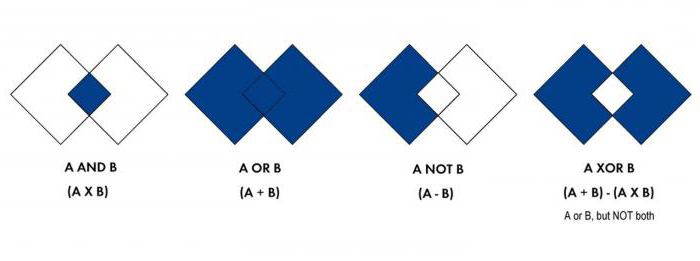
Všeobecné podmínky

Dnes je logika studována ve formě matematické logiky. Je založen výhradně na formálních metodách poznání. Jednou z klíčových částí směru je algebra logiky. Specializuje se pouze na složité objekty a metody, které vám umožňují nastavit jejich parametry. Používá se přísně algebraické způsoby učení.

Věda se nazývá booleovská algebra, protože je její autor George Boole, formuloval své hlavní myšlenky v roce 1854, když vydal základní knihu. Boule si stanovil úkol studovat operace, na jejichž základě funguje lidská mysl, porozumět mechanismu uvažování a popisovat to pomocí symbolů. Po dosažení tohoto úspěchu se mu podařilo vytvořit novou vědu.

Logické výrazy v programování

Podmíněný logický výraz jsou některé proměnné a konstanty, které jsou klasifikovány jako jednoduché. Všechny objekty jsou porovnávány navzájem. . V důsledku výpočtu je možné získat určitý konečný podmíněný výraz: pravdivý nebo nepravdivý .

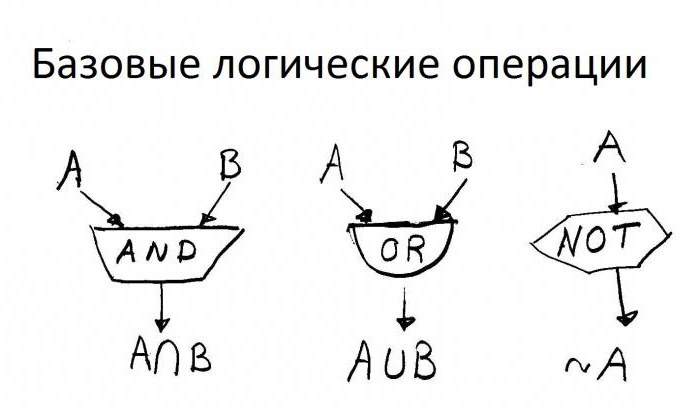
Nejvíce použitelná logika v programování. Pomocí příkladu Pascalu můžeme rozlišit nejdůležitější operace použité v praxi:

• definice většího ze dvou;
• definice menšího ze dvou;
• výpočet menší nebo roven;
• výpočet větší nebo roven;
• definice rovnosti dvou výrazů;
• závěr, že výrazy nejsou stejné.

Pokud je během programování nutné vytvořit logický výraz, ale vzájemně se porovnávají reálná čísla, je třeba vzít v úvahu následující skutečnost: reprezentace čísel je nepřesná, protože zaokrouhlování je nezbytné. To znamená, že operace výpočtu přísné rovnosti nemůže být přesná. Zkušení programátoři doporučují, aby se zabránilo přístupu k této operaci, pokud je to možné, protože je pravděpodobné, že rovnost bude nakonec považována za falešnou, aniž by byla taková.

Příklad: x = (2,23 * x / 2,23)

Souhlasíte, pravdivost vzorce je vizuálně viditelná. Ale při psaní do kódu počítače a nevyhnutelnosti zaokrouhlení chyby ve výpočtech, to bude nepravdivé.

Další jemný bod: podmíněný logický výraz je nutně zapsán do závorek, pokud je operand. Pravidlo vychází z rozvinuté hierarchie operací. Například srovnání v jeho prioritě je nižší než ostatní a logické operace jsou vysoké. . Chcete-li změnit způsob výpočtu konkrétního příkladu vzhledem k takové objednávce, je nutné umístit závorky .

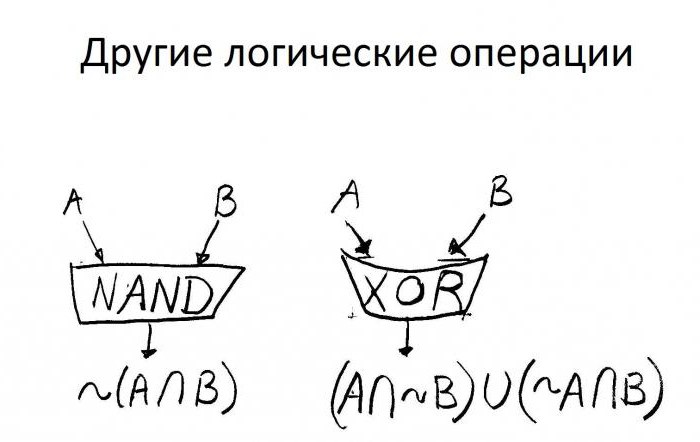
Základy vědy

Objekt v logice je obecně chápán jako vyprávění, které je přesně hlášeno, že je to lež, pravda. Hodnota logického výrazu, je-li pravdivá, je zapsána jako jedna, druhá volba je označena nulou.

Při logických operacích se běžně chápou takové akce (zpravidla myšlený proces), které nakonec dávají zvýšení znalostí a také vedou k vytvoření zcela nových objektů.

Logický výraz je ústní, můžete jej zapsat. Je součástí objektů spolu s konstantami. Výraz přímo závisí na proměnných objektů, čímž se stává jeden nebo nula.

Pokud byste museli řešit složité tvrzení, musíte si uvědomit, že obsahuje složité jednoduché výrazy, pro které byly použity logické operace.

Logika identifikuje klíčové operace nazvané:

• spojení;
• rovnocennost;
• disjunkce;
• implikace;
• inverze

. Vyřešit téměř všechny příklady z nich stačí .

Spojení

Tento termín je běžně chápán jako taková složitá operace, která může být pravdivá pouze tehdy, jsou-li oba jednoduché komponenty pravdivé. Jiné možnosti jsou považovány za nepravdivé.

Je napsán jako: F = A & B.

Tabulka:

Rozdělení

V této situaci je pravdivost logických výrazů určována na základě analýzy hodnoty (jedné a nuly) složek jednoduchých výrazů. Pokud jsou obě hodnoty false, funkce má také hodnotu nula. Jinak je jeho hodnota jedna.

Je napsán jako: F = A + B.

Tabulka:

Inverze

Termín odkazuje na operaci, když se změní na falešný výraz, který byl dříve pravdivý, a naopak. Je-li zdrojový objekt správný, výsledek je falešný a pokud byla zpočátku lož, změní se na pravdu.

Tabulka:

Ekvivalence

Tento logický výraz bude znamenat pouze jeden, pokud oba výrazy v příkladu znamenají stejnou věc.

Tabulka:

Důsledky

Termín je aplikován na takový složitý výraz logiky, který je falešný, pokud z pravdy vyplývá nepravda. Další situace: hodnota se rovná jedné. Operace je aplikována na dva jednoduché objekty, z nichž jeden se nazývá stav a druhý je důsledkem.

Tabulka:

Operace: logické nuance

Pokud znáte, jaký logický výraz se používá jako objekt, můžete výsledek správně vypočítat. Současně je třeba si uvědomit, že operace v logice jsou, stejně jako v aritmetice, operace, které jsou nezbytné pro interakci s čísly. . Logické operace pomáhají budovat logické výrazy - to je také paralelní s algebrou .

Jako součást logických výrazů jsou konstanty a proměnné. První mají určitou hodnotu - nula nebo jedna. Pokud výraz obsahuje některé proměnné, nastaví tak logickou funkci, jejíž hodnota je vypočítána na základě argumentů. Hodnoty argumentů pro jednotlivé úlohy jsou specifikovány v podmínkách. Stačí je nahradit výrazem a pak provedete další výpočet.

Jakýkoli logický výraz může mít vlastní pravdivostní tabulku, tj. Objekt, který detailně popisuje ve všech variantách, které hodnoty a kdy funkce akceptuje, pokud se používá určitá sada proměnných. Jeden řádek takového stolu představuje jeden soubor výchozích podmínek pro výpočet. . Jsou-li do funkce zahrnuty N proměnné, existuje dvakrát více řádků .

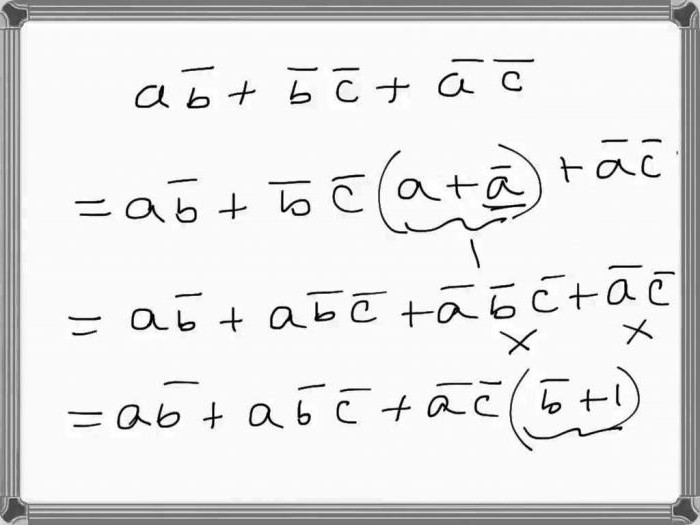
Pravdivé tabulky

Ve všech tabulkách jsou charakteristické následující obecné vlastnosti:

• počet již zmíněných řádků, dvojnásobek počtu proměnných;
• Počet sloupců v tabulce je o více než počet proměnných.

Bez ohledu na to, co je množina proměnných hodnot daných ve stavu, lze vždy formulovat výraz, který se bude rovnat jednomu z určité množiny proměnných.

Nahrává se jako "rozdělení spojení". V praxi to znamená, že můžete vytvořit určitý výraz, který má připravený pravdivý stůl před vámi. Samozřejmě, objem této tabulky může výrazně komplikovat úkol matematiky.

Zjednodušte

Často existují situace, kdy matematický výraz vyžaduje zjednodušení pro přiměřenost řešení. Existují určité konverze, které jsou použitelné v booleovské logice.

Zejména jeden výraz může být nahrazen jiným výrazem, který je ekvivalentní. Zkontrolujte rovnocennost analýzou pravdivých tabulek. Pokud se shodují, můžete je nahradit. . Zde platí falešné pravidlo, když se v objektu A změní na nějakou subexpresi P, která byla přítomna před Q, a byl získán výraz B. Ve všech výpočtech je to ekvivalent A.

Zjednodušení logických výrazů se obvykle nazývá minimalizace. Hlavním úkolem minimalizace je reprezentovat funkci v takové podobě, když jsou písmena, operace, nejmenší možný počet. Můžete dosáhnout požadované jedné ze dvou možností:

• algebraické;
• grafické.

Algebraická metoda

Logický výraz lze zjednodušit algebraickou metodou zjednodušením vzorce. To je provedeno ekvivalentními transformacemi, které již byly popsány výše. V tomto případě je třeba vzít v úvahu identity a pravidla, které existují v booleovské algebře.

Zjednodušený výraz od toho, který byl původně vyřešen, se liší především počtem písmen. Existují však často problémy, když musíte prokázat rovnocennost původního výrazu a výsledné zjednodušení. To se provádí porovnáním pravdivých tabulek.

Pokud příklad předkládá základní výkazy, můžete dosáhnout jejich změny, a to nejen obecných pravidel, ale také těch, které se vztahují k operacím na souborech.

Při analýze výkazů souvisejících se soubory je často nejlepší možností snížit výrazy na důsledek, když členové již neobsahují důsledky.