Proudový proud v elektrických obvodech

Jeden z parametrů charakterizujících chování elektronů v elektrickém obvodu, kromě napětí a proudu, je výkon. Jedná se o míru práce, kterou lze provést za jednotku času. Práce se obvykle porovnává s zvednutím hmotnosti. Čím větší je hmotnost a výška jejího vzestupu, tím více práce se děje. Napájení určuje rychlost pracovní jednotky.

Jednotky míry

Výkon vozidla se vypočítá v koňské síle - měrnou jednotku vynalezenou výrobci parní stroje aby bylo možné měřit výkonnost jejich jednotek v obvyklém energetickém zdroji daného času. Síla auta neříká, jak vysoká může dosáhnout kopce nebo jakou váhu může nést, ale pouze ukazuje, jak rychle to učiní.

Výkon motoru závisí na rychlosti a kroutícím momentu výstupního hřídele. Rychlost se měří v otáčkách za minutu. Krouticí moment je okamžik výkonu motoru, který byl naměřen zpočátku v lb-ft a nyní v nových metrech nebo joulech.

100 l traktorového motoru c. otáčí se pomalu, ale s velkým kroutícím momentem. Motocykl stejného motoru se rychle otáčí, ale s mírným kroutícím momentem. Rovnice výpočtu výkonu má podobu:

P = 2π ST / 33000, kde S je rychlost otáčení, ot / min a T je točivý moment.

Proměnné jsou moment a rychlost. Jinými slovy, výkon je přímo úměrný ST: P ~ ST.

DC napájení

V elektrických obvodech je výkon funkčně závislý na napětí a proudu. Není divu, že je podobná výše uvedené rovnici P = IU.

Ale zde P není úměrný proudu násobenému napětím, ale rovná se. Vypočítává se ve wattech, zkráceně jako W.

Je důležité vědět, že proud a napětí samostatně neurčují výkon, ale pouze jejich kombinaci. Napětí pracuje na jednotku elektrický náboj a aktuální je rychlost poplatků. Napětí (ekvivalent práce) je podobné práci při zvedání hmotnosti v protikladu k síle gravitace. Proud (ekvivalentní rychlosti) je podobný rychlosti zvedání. Jejich práce je síla.

Stejně jako traktory a motocykly, vysokonapěťový obvod s malým proudem může mít stejnou sílu jako obvod s nízkým napětím a vysoký proud. Napětí a proud mimo vztah nemohou charakterizovat sílu obvodu.

Otevřený obvod s napětím a nulovým proudem nefunguje, bez ohledu na výšku napětí. Koneckonců podle vzorce, cokoli vynásobený 0 dává 0: P = 0 U = 0. V uzavřeném obvodu supravodivého drátu s nulovým odporem může být dosaženo proudu při napětí rovném nule, které také nevede ke ztrátě energie: P = I 0 = 0.

Koně a watty označují jedno a to jedno: množství práce, kterou lze provést za jednotku času. Tyto jednotky jsou vzájemně propojeny poměrem

1 l. c. = 745,7 W

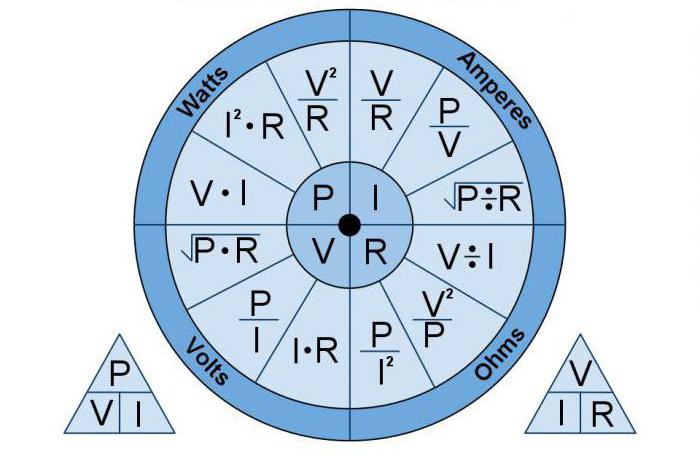
Příklad výpočtu

Výkon elektrického obvodu ve wattech se tedy rovná součinu napětí a proudu.

K určení například zátěžového výkonu 3 ohmů v obvodu s baterií 12 V je nutné pomocí Ohmova zákona najít aktuální

I = U / R = 12/3 = 4 A

Vynásobte proudovou sílu napětí a dáte požadovaný výsledek:

P = IU = 4 A 12 V = 48 W

Lampa tedy spotřebuje 48 wattů.

Co se stane, když se napětí zvýší?

S napětím 24 V a proudem 3 ohmů

I = U / R = 24/3 = 8 A

Při zdvojnásobení napětí se amperage zdvojnásobila.

P = IU = 8 A 24 V = 192 W

Výkon se také zvýšil, ale více. Proč Vzhledem k tomu, že je funkce produktu napětí na proudu, napětí a proudu zvýšena 2x, proto se výkon zvýšil 4krát. To lze ověřit rozdělením 192 wattů na 48, jehož podíl je 4.

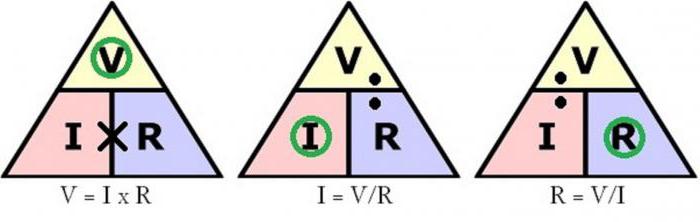
Varianty vzorce

Použitím algebry k transformaci vzorce můžete vzít původní rovnici a transformovat ji v případech, kdy jeden z parametrů není znám.

Jsou-li uvedeny napětí a odpor:

P = (U / R) U nebo P = U ² / R

S známou silou a odolností:

P = I (IR) nebo P = I2R

Historický fakt: vztah mezi rozptýleným výkonem a proudem prostřednictvím odporu objevil James Prescott Joule, ne Georg Simon Simon Om. To bylo vydáno v 1841 jako rovnice P = I ² R a je nazýván Joule-Lenz zákon.

Power rovnice:

• P = uživatelské rozhraní
• P = I2R
• P = U ² / R

Střídavý proud

Zákony Ohm a Joule - Lenz byly zřízeny stejnosměrný proud ale platí i pro okamžité hodnoty měnícího se proudu a napětí.

Okamžitá hodnota P se rovná součinu okamžitých hodnot proudu a napětí s ohledem na jejich fázový posun o úhel φ:

P (t) = U (t) I (t) = U _m cos ω I _m cos (ωt-φ) = (1/2) U _m I _m φ φ + φ).

Z rovnice vyplývá, že okamžitý výkon má konstantní složku a provádí oscilační pohyby kolem průměrné hodnoty s frekvencí, která je dvakrát vyšší než frekvence proudu.

Průměrná hodnota P (t), která je praktického zájmu, je:

P = (U _m Já mám / 2) cosφ

Vzhledem k tomu, že cos φ = R / Z, kde Z = (R ² + (ω L - 1 / ω C) ² ) ^1/2 a U _m / Z =

P = (RI _m ² ) / 2

Zde I = I _m 2 ^-1/2 = 0.707 I _m - efektivní hodnota proudové síly, A.

Podobně U = U _m 2 ^-1/2 = 0,707 U _m - efektivní napětí, V.

Průměrný výkon přes efektivní napětí a proud je určen pomocí

P = UI cos φ, kde cos φ je výkonový faktor.

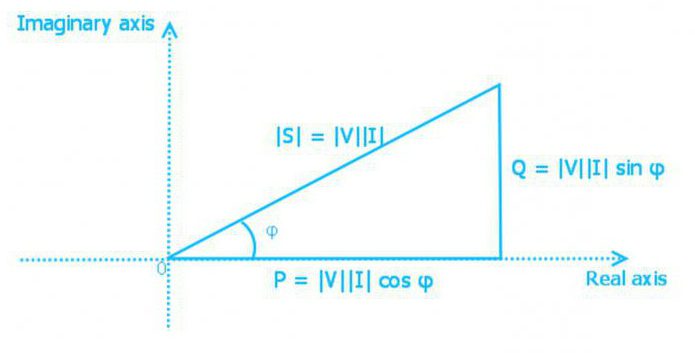
P v elektrickém obvodu jde do tepla nebo jiné formy energie. Nejvyšší dosažitelný výkon lze dosáhnout při cosφ = 1, tj. Při absenci fázového posunu. Říká se tomu plná síla.

S = UI = ZI2 = U2 / Z

Jeho rozměr se shoduje s rozměrem P, ale pro účely rozdílu S se měří pomocí voltampérů, VA.

Stupeň výměny energie v elektrickém obvodu je charakterizován reaktivním výkonem.

Q = UI sinφ = UI _p = U _p I = XI ² = U ² / X

Má rozměr aktivního a úplného, ​​ale pro rozlišení je vyjádřen reaktivními voltovými ampere, VAR.

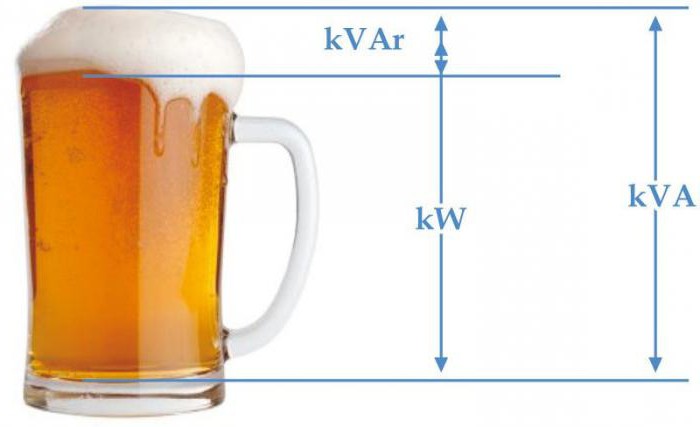
Výkonný trojúhelník

Napájení je aktivní, reaktivní a plně propojené

S = (P2 + Q2) ^1/2

Výkon představuje stranu pravý trojúhelník. Pomocí zákonů trigonometrie lze nalézt délku jedné strany (množství síly libovolného typu) podél dvou známých stran nebo po délce jedné a úhlu. V takovém trojúhelníku je aktivní síla sousední noha, reaktivní síla je opačná a celkový výkon je hypotenze. Úhel mezi koncem aktivní energie a hypotenzou se rovná fázovému úhlu impedance Z elektrického obvodu.

Komplexní forma tohoto vztahu je následující:

S = P + jQ = UI cosφ + j UI sinφ = UI e ^jφ = UI *, kde

S je složitá síla;

I * je komplexní hodnota konjugovaného proudu.

Skutečná složka komplexu je aktivní a imaginární je reaktivní.

Okamžitý celkový výkon zůstává vždy konstantní.

Třífázový výkon

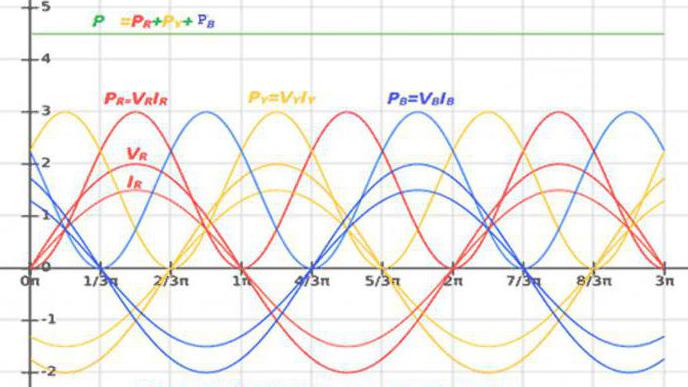
Zatížení každé fáze třífázového obvodu přeměňuje energii nebo ji vyměňuje za zdroj energie. Výsledkem je, že obvody P a Q se rovnají celkovému výkonu všech fází:

P = P _r + P _y + P _b ; Q = Q _r + Q _y + Q _b - hvězda připojení;

P = P _ry + P _yb + P _br ; Q = Q _ry + Q _yb + Q _br - připojení "trojúhelník".

Aktivní a reaktivní síly každé fáze jsou definovány jako v jednomfázovém okruhu.

Celý výkon třífázového okruhu:

S = (P2 + Q2) ^1/2 ,

co vypadá v složité podobě

S = P + jQ = (P _r + P _y + P _b ) + j (Q _r + Q _y + Q _b ) = S _r + S _y + S _b = U _r I _r + U _y I _y + I _b

Symetrické zatížení fází vede k rovnosti jejich pravomocí. Proto je síla proudu třikrát účinná a reaktivní síla fáze:

P = 3P _f = 3 I _f U _f cosφ _f = 3 R _f I _f ²

Q = 3 Q _f = 3 I _f U _f sin _{f f} = 3 X _f I _f ²

S = 3 S _f = 3 I _f U _f

I _f a U zde mohou být nahrazeny jejich lineárními hodnotami, vzhledem k tomu, že pro hvězdu U _f = U _l ; I _f = I _l a pro trojúhelník U _f = U _l ; I _f = I _l 3 ^-1/2 :

P = 3 ^1/2 I _l U _l cosφ _f ;

Q = 3 ^{1/2 I _l U _l} sinφ _f ;

S = 3 ^{1/2 I _l U _l} .

Nesinusový proud

Definice P v nesynosečním proudovém obvodu je podobná jeho definici v obvodu sinusového proudu, protože v průběhu doby T je průměrný okamžitý výkon

P = 1 / Tcui dt

Aktivní výkon proudu je určen součtem harmonických složek P, včetně konstanty, která je harmonickou nulovou frekvencí.

Reaktivní výkon proudu tímto způsobem je výsledkem přidání Q každé harmonické.

Q = ΣU _k I _k sinφ _k = Q _k

Celkový výkon je určen produktem účinného proudu a napětí:

S = I U.