Desítkové zlomky a akce s nimi. Desetinné dělení a násobení

Desítková zlomka se používá, když potřebujete provádět akce s nečíselnými čísly. To se může zdát nesmyslné. Ale tento druh čísel velmi usnadňuje matematické operace, které je třeba s nimi provádět. Toto porozumění přichází s časem, když se jejich záznam seznámí a čtení nevyvolává potíže a pravidla desítkových zlomků se zvládnou. Navíc jsou již známy všechny opakované akce, na které se dozvídáme přirozených čísel. Stačí si pamatovat některé funkce.

Definice desítkové frakce

Desetinná zlomka je zvláštní reprezentace necelového čísla s jmenovatelem, který je dělitelný deseti a odpověď je získána jako jednotka a případně s nulami. Jinými slovy, pokud je jmenovatel 10, 100, 1000 a tak dále, je vhodnější přepisovat číslo pomocí čárky. Pak bude před ním umístěna celá část a pak část. Nahrávání druhé poloviny čísla bude navíc záviset na jmenovateli. Počet číslic, které jsou ve zlomkové části, by se měl rovnat řadě jmenovatele.

Vysvětlete výše s těmito čísly:

9/10 = 0,9; 178/10000 = 0,0178; 3,05; 56 003,7006.

Důvody pro použití desetinných zlomků

Matematici vzali desetinné zlomky z několika důvodů:

1. Zjednodušte nahrávání. Taková zlomka je umístěna podél jedné linky bez pomlčky mezi jmenovatelem a čitatelem, zatímco viditelnost netrpí.

2. Jednoduchost v porovnání. Stačí, když porovnáte čísla ve stejných pozicích, zatímco s obyčejnými zlomky byste je museli přenést na společného jmenovatele.

3. Zjednodušte výpočty.

4. Kalkulačky nejsou určeny pro zavedení obyčejných zlomků, pro všechny operace používají desetinnou notaci.

Jak číst tato čísla?

Odpověď je jednoduchá: stejně jako obyčejné smíšené číslo s jmenovatelem násobkem 10. Jedinou výjimkou jsou zlomky bez celočíselných hodnot, pak při čtení je třeba vyslovovat "nulové celočíselné hodnoty".

Například 45/1000 by mělo být vyslovováno jako čtyřicet pět tisícin , zatímco 0.045 bude znít jako nulový bod čtyřicet pět tisícin .

Smíšené číslo s celočíselnou částí rovnou 7 a zlomek 17/100, které je napsáno jako 7.17, v obou případech bude čteno jako sedmnáct sedmnáct setin .

Úloha vypouštění ve frakcích

Je pravda, že označuje propuštění - to je to, co vyžaduje matematika. Desítkové zlomky a jejich hodnota se mohou významně změnit, pokud zapíšeme číslo na nesprávné místo. To však bylo pravdou.

Chcete-li číst číslice celé desetinné čárky, stačí použít pravidla známá pro přirozená čísla. A na pravé straně jsou zrcadlí a číst jinak. Pokud se v celé části ozve "desítky", pak za čárkou bude již "desetiny".

Je zřejmé, že to lze vidět v této tabulce.

Jak psát smíšené číslo v desítkové?

Je-li jmenovatel číslem rovným 10 nebo 100 a jiným, pak otázka, jak převést zlomek na desetinnou hodnotu, je jednoduchá. Chcete-li to provést, stačí přepsat všechny jeho součásti jiným způsobem. To pomůže těmto bodům:

• trochu stranou zapisovat čitatel zlomku, v tomto okamžiku je desetinná čárka vpravo, za poslední číslicí;

• přesuňte čárku doleva, nejdůležitější je správné počítání čísel - musíte je přesunout na tolik poloh, kolik je v jmenovateli nuly;

• pokud chybí, prázdné pozice by měly být nuly;

• nuly, které byly na konci čitatele, již nejsou potřebné a mohou být zkřížené;

• Před čárkou, která přidělí celočíselnou část, pokud by nebyla, pak bude také nula.

Pozor. Nemůžete překročit nuly, které byly obklopeny jinými čísly.

Jak se dostat do situace, kdy číslo v jmenovateli není pouze od jedné a nula, jak převést zlomek na desetinnou, můžete si přečíst trochu níže. To jsou důležité informace, které byste si měli určitě přečíst.

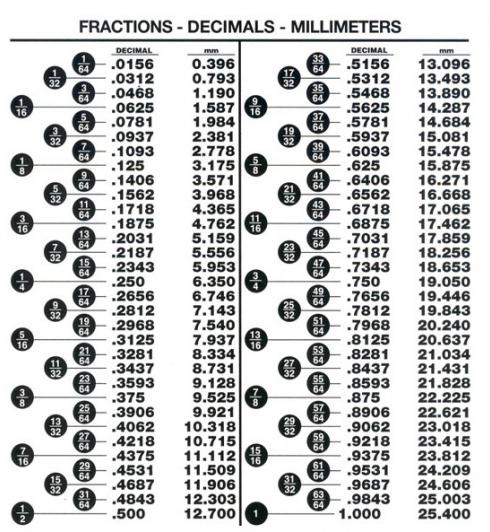
Jak převést zlomek na desetinnou hodnotu, je-li jmenovatel libovolným číslem?

Jsou zde dvě možnosti:

1. Když jmenovatel může být zastoupen jako číslo, které je deset libovolného stupně.

2. Není-li taková operace možná.

Jak to kontrolovat? Je nutné rozšířit jmenovatele na faktory. Pokud je ve výrobku pouze 2 a 5, pak je vše v pořádku a zlomek lze snadno převést na konečné desetinné místo. V opačném případě se zobrazí 3, 7 a další primární čísla pak bude výsledek nekonečný. Taková desetinná část pro snadné použití v matematických operacích je obvykle zaoblená. To bude popsáno níže.

Studie o tom, jak jsou tyto desítkové frakce získány, stupeň 5. Příklady zde budou velmi užitečné.

Nechť jmenovatelé jsou čísla: 40, 24 a 75. Rozklad na primární faktory pro ně budou:

• 40 = 2, 2, 2, 5;
• 24 = 2, 2, 2, 3;
• 75 = 5,5,3.

V těchto příkladech může být pouze první zlomek zastoupena jako konečná.

Algoritmus pro konverzi běžné frakce na konečné desetinné čárky

• Zkontrolujte rozšíření jmenovatele na primární faktory a ujistěte se, že bude sestávat z 2 a 5.

• Přidejte k těmto číslům až 2 a 5, aby se staly stejným číslem. Poskytnou hodnotu dodatečného faktoru.

• Vynásobit jmenovatelem a čitatelem tímto číslem. Výsledkem je obyčejná zlomka, jejíž čára je do určité míry 10.

• Pokračujte tak, jak je popsáno v odstavci, umístěné o něco výš.

Pokud v úkolu jsou tyto akce prováděny se smíšeným číslem, musí být nejprve zastoupeny jako zlý zlomek. A teprve potom jednat podle popsaného scénáře.

Zastupování společného zlomku ve formě zaokrouhlených desetinných míst

Tento způsob, jak převést zlomek na desetinnou, bude pro někoho jednodušší. Protože nemá velký počet akcí. Je nutné pouze rozdělit hodnotu čitatele jmenovatelem.

K libovolnému číslu s desetinnou čárkou napravo od čárky můžete přiřadit nekonečný počet nul. Tato vlastnost a potřebují používat.

Nejprve napište celou část a za ni vložte čárku. Je-li zlomek správný, pak zadejte nulu.

Poté je nutné čitateli rozdělit podle jmenovatele. Takže jejich počet je stejný. To znamená přidat požadovaný počet nul vpravo od čitatele.

Proveďte dělící se bar až do požadovaného počtu číslic. Například, pokud potřebujete zaokrouhlit až na stotiny, pak by měla odpovídat 3 odpovědi. Obecně by mělo být ještě jedno číslo, než je třeba nakonec získat.

Zaznamenejte mezitím odpověď za čárkou a zaokrouhlete ji podle pravidel. Je-li poslední číslice od 0 do 4, stačí ji spustit. A když se rovná hodnotě 5-9, musí být jedna před tím zvýšena o jednu a vyřazena.

Návrat z desetinné frakce na obyčejnou

V matematice existují problémy, kdy desetinné zlomky jsou pohodlněji prezentovány jako běžné, v nichž je čitatel s jmenovatelem. Můžete vydechnout úlevu: tato operace je vždy možná.

Pro tento postup proveďte následující:

• napište celočíselnou část, pokud je nula, pak nemusíte psát nic;

• nakreslit řádek;

• nad ním zapíše čísla z pravé strany, jestliže první jsou nuly, pak je třeba je zkřížit;

• pod řádkem zapište jednotku s nulami nulou jako počet číslic za desetinnou čárkou v počáteční frakci.

Toto je vše, co musíte udělat, abyste přepočítali desítkovou frakci na obyčejnou.

Co lze provést s desítkami zlomků?

V matematice se jedná o určité akce s desítkami zlomků, které byly dříve provedeny pro jiná čísla.

Jsou to:

• porovnání;

• sčítání a odčítání;

• násobení a rozdělení.

První akce, srovnání, je podobná tomu, jak bylo provedeno pro přirozená čísla. Chcete-li zjistit, který z nich je větší, je třeba porovnat výboje celé části. Pokud se ukáží, že jsou rovnocenné, pak jdou na zlomkové a také je porovnají v pořadí číslic. Toto číslo, kde bude velká postava v seniorské kategorii, bude také odpovědí.

Přidání a odečítání desetinných zlomků

To jsou snad nejjednodušší akce. Protože se řídí pravidly pro přirozená čísla.

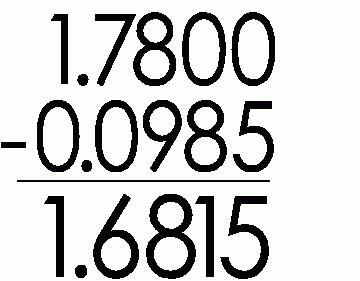
Chcete-li přidat desetinné zlomky, je třeba je zapsat jeden za druhým a zařadit čárky do sloupce. S takovým vstupem vlevo od čárk jsou všechny části a vpravo - zlomkové. A nyní je třeba přidávat čísla jeden po druhém, jak to děláme s přirozenými čísly, klepnutím na čárku. Je třeba začít sčítat z nejmenší kategorie zlomkovou část čísla. Pokud pravá polovina nemá dost čísel, přidejte nuly.

Při odečtení se jedná stejným způsobem. A zde je pravidlo, které popisuje schopnost převzít jednotku z vyšší úrovně. Pokud je desítková zlomka má méně číslic než odpočitatelná, pak jsou nuly jednoduše přiřazeny.

Trochu komplikovanější je případ s úkoly, kde musíte provádět násobení a rozdělení desítkových zlomků.

Jak rozdělit desetinnou frakci v různých příkladech?

Pravidlo, podle kterého se množí desetinné zlomky podle přirozeného čísla, je:

• napište je do sloupce, nevěnujte pozornost čárce;

• množit se, jako by byly přirozené;

• oddělené čárky s tolika číslicemi, které byly v částečné části původního čísla.

Zvláštním případem je příklad, ve kterém je přirozené číslo 10 libovolného stupně. Poté, abyste získali odpověď, stačí přesunout čárku vpravo na tolik polohách, kolik je v jiném multiplikátoru nula. Jinými slovy, když se vynásobí číslem 10, čárka se posune o jednu číslici, o 100 - tam budou dvě, a tak dále. Pokud v částečné části není dostatek číslic, musíte na prázdných polohách psát nuly.

Pravidlo, které se používá v úkolu, je třeba vynásobit desetinné zlomky jiným stejným číslem:

• napište je pod sebe, nevěnujte pozornost čárkám;

• množit se, jako by byly přirozené;

• oddělené čárky s tolika číslicemi, které byly ve frakčních částech obou původních frakcí dohromady.

Zvláštním případem jsou příklady, kdy jeden z faktorů se rovná 0,1 nebo 0,01 a více. Musí přesunout čárku vlevo o počet číslic v prezentovaných násobcích. To znamená, že pokud je vynásobeno číslem 0,1, čárka se posune o jednu pozici.

Jak rozdělit desetinnou čárku v různých úlohách?

Rozdělení desetinných zlomků na přirozené číslo se provádí podle následujícího pravidla:

• napište je na rozdělení do baru, jako by byly přirozené;

• rozdělit podle obvyklého pravidla, dokud celá část neskončí;

• vložte čárku do odpovědi;

• pokračujte v dělení frakční složky, dokud se ve zbývající části nedosáhne nuly;

• v případě potřeby můžete přiřadit požadovaný počet nul.

Je-li celočíselná část nula, pak nebude ani v odpovědi.

Odděleně je rozdělení na čísla deset, stovek a tak dále. V takových úkolech musíte přesunout čárku vlevo o počet nul v děliči. Stává se, že v celočíselné části není dostatek číslic, místo toho se použijí nuly. Vidíte, že tato operace je podobná vynásobení číslem 0,1 a podobným číslům.

Chcete-li provést desítkové zlomky, musíte použít toto pravidlo:

• přeměňte dělitele na přirozené číslo a pro tento pohyb posuňte čárku vpravo na konec;

• přesuňte čárku a v dividendě stejným počtem číslic;

• postupujte podle předchozího scénáře.

Vystupte rozdělení o 0,1; 0,01 a další podobná čísla. V takových příkladech je čárka posunuta napravo o počet číslic ve zlomkové části. Pokud skončí, musíte přidat chybějící počet nul. Stojí za zmínku, že tato akce opakuje rozdělení o 10 a podobné čísla.

Závěr: je to všechno o praxi

Nic v škole není snadné a bez námahy. Pro spolehlivý vývoj nového materiálu je zapotřebí času a školení. Matematika není výjimkou.

Aby téma desetinných zlomků nevyvolalo potíže, je třeba s nimi co nejvíce řešit příklady. Koneckonců, tam byl čas, kdy přidání přirozených čísel zmateno. A teď je všechno v pořádku.

Proto, abychom parafrázovali známou frázi: rozhodněte se, rozhodněte se a vyřešte znovu. Pak úkoly s takovými čísly budou prováděny snadno a přirozeně, jako další puzzle.

Mimochodem, hádanky jsou zpočátku obtížné vyřešit, a pak je potřeba znát pohyby. Je to stejné v matematických příkladech: po několika krocích několikrát, pak už nebudete přemýšlet o tom, kam se obrátit.