Desetinné zaokrouhlování: učení matematika

Takže teď s vámi uvidíme, jak se desetinná zaokrouhlení odehrává. Ve skutečnosti není tento proces tak složitý, jak se na první pohled může zdát. Je pravda, že někteří školáci mají problémy s tímto tématem. Pomozme jim pochopit naši dnešní otázku.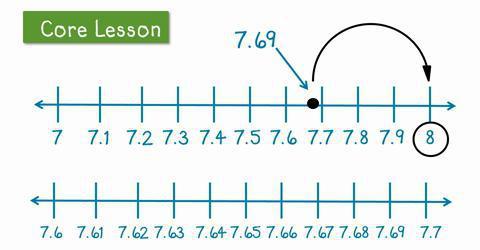

Pojem desítkové zlomky

Před zaokrouhlováním desetinná místa, musíme jasně pochopit, s čím musíme vypořádat. Čím lépe tuto otázku s vámi rozumíme, tím snadněji bude v budoucnu.

Obecně platí, že pojem "desetinné zlomky" se objevuje v 5. ročníku školy. Jedná se o určitý počet, který se skládá z celé a částečné části, jejíž jmenovatel je 10.

Abychom jasně porozuměli, co je v sázce, podívejme se na příklad a pak se podívejme, jak zaokrouhluje desetinná místa. Tento typ záznamu bude vypadat takto: 5,26852. Pokud výsledné číslo překládáte na zlomek, můžete vidět následující: 526852/100000. Desítkové zlomky mohou být pozitivní i negativní. To je všechno. Teď pojďme s vámi na náš problém.

V částech

Bodem je, že zaokrouhlení desetinných zlomků (stupeň 6) se zpravidla vyskytuje v částech. Za prvé, zabírají zbytek ("ocas"), tj. Čísla, která jsou za čárkou. Teprve pak je možné počítat s celou částí.

První věc, která se od nás požaduje, je určit přesnost, s jakou zaokrouhlujeme desetinné zlomky. Až desetiny, stotiny, tisíce a tak dále. Pak musíte dodržovat některá pravidla, stejně jako naučit se jeden důležitý bod, který vám určitě pomůže vyrovnat se s úkolem. Pracujeme s vámi s jasným příkladem. Vezměte si libovolné číslo: 78,9563245. Na tom budeme testovat pravidlo zaokrouhlení desetinných míst. Teď ho poznáme.

Hlavní pravidlo

Základní princip, který se musíme naučit, je, jak nahradit čísla při zaokrouhlování. Věc je, že je to celkem snadné. Uvidíme přesně jak.

Pokud máte 0, 1, 2, 3 nebo 4 jako číslici, je automaticky nahrazeno číslem 0 a vyřazeno. Dále přejděte blíže k celočíselné části a podívejte se na další číslo.

Jakmile je číslice v číslici 5, 6, 7, 8 nebo 9, musíte tuto část zlikvidovat a přidat jednu do další (nejblíže k celé části). Tento proces musí být opakován až po zvolenou přesnost zaokrouhlení. Podívejme se nyní na příklad s vámi. Na tom bude vše vypadat jasněji.

Příklad

Takže začneme s vámi zaokrouhlovat desetinná místa. Pracujeme s číslem 78,9563245. Zaokrouhlujeme to na desátou, stotinu a tisíciny. Zkusme to.

Začneme tím, že zlikvidujeme celou část. Máme 0.9563245. Budeme i nadále spolupracovat s vámi s tímto konkrétním číslem. Začneme zaokrouhlovat s tisícinami, postupně zvyšujeme přesnost.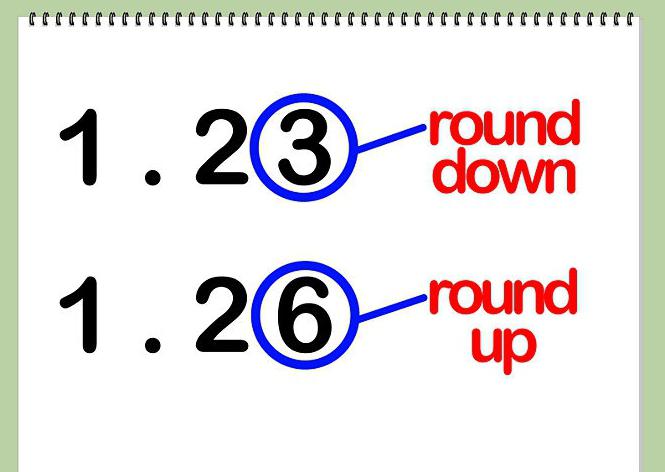

Číslo je 0.9563245. Přesun na nulu. První číslo z konce je 5. To znamená, že jej "konvertujeme" na 0 a přidáme 4 až 4. Druhá číslice - 4 + 1 = 5. Proto přiřadíme k dalšímu znaku jednotku a tato je převedena na 0.

Zatím jsme s vámi pracovali: 0.95632 ⁽⁺¹⁾ . Zaokrouhlování na tisícinu je 3 číslice. Pokračujte ve spolupráci s vámi. 2 + 1 = 3. Tento údaj je menší než 5s. Takže nahraďte ji 0 a odstraňte. Dalším krokem je 3-ka. Nic není přidáno. Stačí nahradit 0, protože je menší než 5. Udělali jsme to s vámi: 0.956. Nyní můžete přidat celou částku: 78 956.

Ale naše zaokrouhlení desetinných zlomků zde nekončí. Nyní byste ji měli držet na stotinu. Abychom to mohli udělat, stejně jako předtím se podíváme na poslední číslici za čárkou - 6. Podle pravidla jej nahrajeme 0 a pak jednoduše přidáme 1 k číslici nalevo od ní. Získáme 78,96. Zaokrouhlování až desetin tu není příliš vhodné. Získáme s sebou celé číslo. Koneckonců bude 6-ka nahrazen číslem 0, jednotka bude přidána na 9 a nakonec dostaneme: 78,9 ⁽⁺¹⁾ . Ukáže to 79. To je všechno. Nyní víte, jak oblékat zlomky.