Diskriminační: příklady řešení. Jak řešit kvadratické rovnice prostřednictvím diskriminačního

Čtvercové rovnice se často objevují při řešení různých problémů fyziky a matematiky. V tomto článku se budeme zabývat tím, jak tyto rovnosti řešit univerzálním způsobem "prostřednictvím diskriminačního". Příklady využití získaných poznatků jsou také uvedeny v článku.

O kterých rovnicích mluvíme?

Níže uvedený obrázek ukazuje vzorec, ve kterém x je neznámá proměnná a latinské znaky a, b, c jsou některá známá čísla.

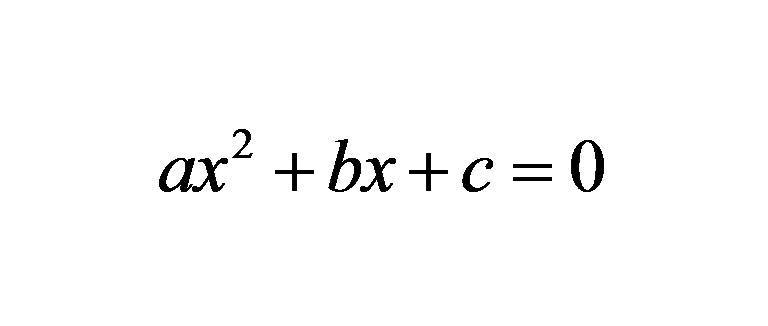
Každý z těchto symbolů se nazývá koeficient. Jak vidíte, číslo "a" stojí před proměnnou x na druhou. Toto je maximální zastoupení výrazu, takže se nazývá kvadratická rovnice. Jeho jiné jméno se často používá: rovnice druhého řádu. Hodnota samotného je čtvercový koeficient (stálý s proměnnou čtvercovou), b je lineární koeficient (je vedle proměnné zvýšené na první sílu) a konečně číslo c je volné termín.

Všimněte si, že typ rovnice, který je znázorněn na obrázku výše, je běžný klasický čtvercový výraz. Kromě toho existují další rovnice druhého řádu, ve kterých mohou být koeficienty b, c nulové.

Když úkolem je vyřešit uvažovanou rovnost, znamená to, že je třeba nalézt takové hodnoty proměnné x, které by ji uspokojily. Zde je třeba nejprve zapamatovat následující věc: jelikož maximální stupeň X je 2, tento typ výrazu nemůže mít více než 2 řešení. To znamená, že pokud při řešení rovnice nalezli dvě hodnoty x, které ji uspokojují, pak si můžete být jisti, že neexistuje třetí číslo, nahrazující místo toho x rovnost by byla pravda. Rovnice řešení v matematice nazývají kořeny.

Způsoby řešení rovnic druhého řádu

Řešení rovnic tohoto typu vyžaduje znalost některé teorie o nich. Ve školním kurzu algebry jsou zvažovány 4 různé metody řešení. Seznamujeme je:

• pomocí factorizace;
• pomocí vzorce pro celé čtverec;
• použití grafu příslušné kvadratické funkce;
• pomocí diskriminační rovnice.

Plus první metodou je jeho jednoduchost, ale nemůže být použita na všechny rovnice. Druhá metoda je univerzální, ale poněkud těžkopádná. Třetí metoda je pozoruhodná z důvodu srozumitelnosti, ale není vždy vhodná a použitelná. A konečně, použití diskriminační rovnice je univerzální a poměrně jednoduchý způsob, jak najít kořeny absolutně jakékoliv rovnice druhého řádu. Proto se v článku zabýváme pouze to.

Vzorec pro získání kořenů rovnice

Podívejme se na obecnou podobu kvadratické rovnice. Napsali jsme to: a * x² + b * x + c = 0. Před použitím metody jeho řešení "přes diskriminační" je nutné snížit rovnost vždy na zaznamenanou formu. To znamená, že musí sestávat ze tří pojmů (nebo méně, pokud b nebo c je 0).

Například pokud existuje výraz: x²-9 * x + 8 = -5 * x + 7 * x², měli byste nejprve přenést všechny jeho členy na stejnou stranu rovnice a přidat rovnoměrné výrazy obsahující proměnnou x.

V tomto případě bude tato operace mít za následek následující výraz: -6 * x²-4 * x + 8 = 0, což je ekvivalentní rovnici 6 * x² + 4 * x-8 = 0 (zde vynásobíme levou a pravou stranu rovnosti -1) .

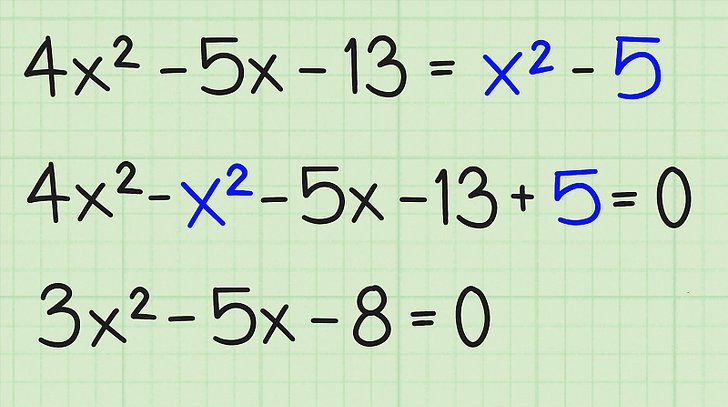
Jakmile se výše uvedený krok učí, měli byste se naučit rozlišovat koeficienty. Všechno je jednoduché zde: když x2 je vždy a, když x ¹ je b, volný c je číslo, které nesouvisí s x.

V příkladu výše, a = 6, b = 4, c = -8. Vezměte na vědomí, že všichni členové posuzované rovnosti jsou vždy sčítáni mezi sebou, takže pokud se objeví znak "-", znamená to, že odpovídající koeficient je záporný, jako v tomto případě.

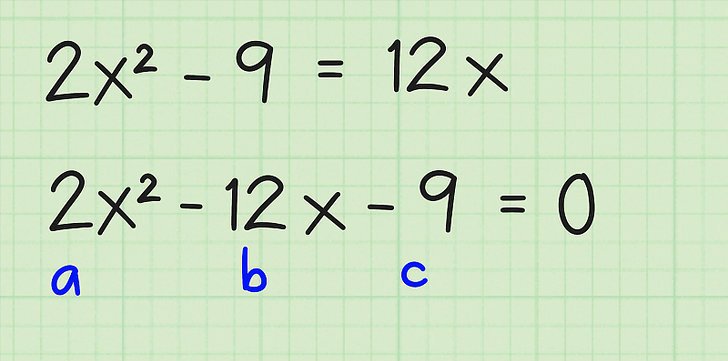
Po analýze tohoto okamžiku se nyní obracíme na samotný vzorec, který umožňuje získat kořeny kvadratické rovnice. Vypadá to, že je zobrazen na fotografii níže.

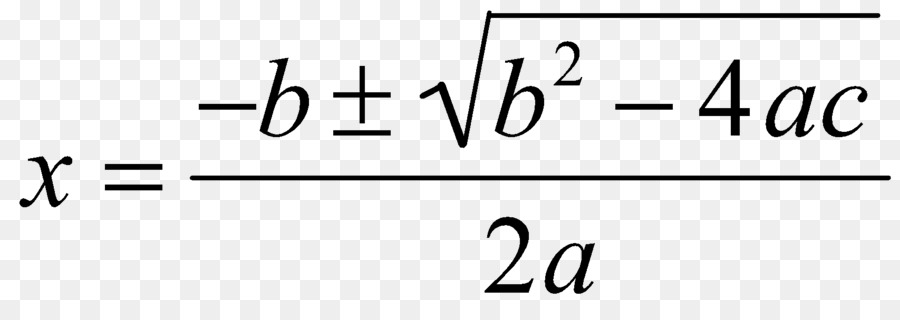
Jak je vidět z tohoto výrazu, umožňuje vám získat dva kořeny (měli byste věnovat pozornost znaménku "±"). Za tímto účelem stačí nahradit koeficienty b, c a a.

Pojem diskriminační

V předchozím odstavci byl uveden vzorec, který umožňuje rychle vyřešit libovolnou rovnici druhého řádu. V něm je kořenový výraz nazýván diskriminační, tj. D = b²-4 * a * c.

Proč je tato část vzorku izolovaná a dokonce má své vlastní jméno? Faktem je, že diskriminující spojuje všechny tři koeficienty rovnice do jediného výrazu. Poslední skutečností znamená, že plně nese informace o kořenech, které lze vyjádřit v následujícím seznamu:

1. D> 0: rovnost má 2 různé řešení, z nichž obě jsou reálná čísla.
2. D <0: získávají se také dva kořeny, ale oba jsou složité. Tento typ výrazu se naučil řešit pouze v renesanci, kdy byl pojem "imaginární jednotky" představen matematiky nové doby.
3. D = 0: rovnice má pouze jeden kořen a je to skutečné číslo.

Článek dále uvádí příklady diskriminačních kvadratických rovnic a jejich řešení.

Úloha stanovení diskriminace

Uvádíme jednoduchý příklad toho, jak najít diskriminaci. Nechte následující rovnost: 2 * x² - 4 + 5 * x-9 * x² = 3 * x-5 * x² + 7.

Přidáme to do standardního formuláře, dostaneme: (2 * x²-9 * x² + 5 * x²) + (5 * x-3 * x) + (- 4-7) + 2 * x-11 = 0. Zde a = -2, b = 2, c = -11.

Nyní můžete použít vzorec pro diskriminaci: D = 2² - 4 * (- 2) * (- 11) = -84. Výsledné číslo je odpovědí na úkol. Protože v příkladu je diskriminátor menší než nula, můžeme říci, že tato kvadratická rovnice nemá žádné skutečné kořeny. Jeho rozhodnutí bude pouze čísla komplexního typu.

Příkladem nerovnosti skrze diskriminaci

Řešíme problémy mírně odlišného typu: daná rovnost je -3 * x²-6 * x + c = 0. Je třeba nalézt hodnoty c, pro které D> 0.

V tomto případě jsou známy pouze 2 ze 3 koeficientů, proto nelze přesně vypočítat přesnou hodnotu diskriminátoru, ale je známo, že je pozitivní. Tato skutečnost se používá při konstrukci nerovnosti: D = (-6) ²-4 * (- 3) * c> 0 => 36 + 12 * c> 0. Řešení výsledné nerovnosti vede k výsledku: c> -3.

Zkontrolujte výsledné číslo. Pro tento účel vypočítáme D pro 2 případy: c = -2 a c = -4. Číslo -2 vyhovuje získanému výsledku (-2> -3), odpovídající diskriminační hodnota bude mít hodnotu: D = 12> 0. Naopak číslo -4 nesplňuje nerovnost (-4 <-3), vypočítáme diskriminační: D = -12 <0, což je v rozporu se stavem problému.

Takže všechna čísla c větší než -3 splňují podmínku.

Příklad řešení rovnice

Představujeme problém, který spočívá nejen v hledání diskriminace, ale iv řešení rovnice. Je nutné najít kořeny pro rovnost -2 * x² + 7-9 * x = 0.

V tomto příkladu se diskriminační hodnota rovná následující hodnotě: D = 81-4 * (- 2) * 7 = 137. Potom jsou kořeny rovnice definovány jako: x = (9 ± √137) / (- 4). Jedná se o přesné hodnoty kořenů, pokud vypočítáme kořen přibližně, pak získáme čísla: x = -5.176 a x = 0.676.

Geometrický problém

Vyřešíme problém, který bude vyžadovat nejen schopnost vypočítat diskriminující, ale i uplatnění dovedností abstraktního myšlení a znalostí, jak vytvořit kvadratické rovnice.

Bob měl přikrývku, která pokrývala 5 x 4 metry. Chlapci se mu chtěli šít kolem obvodu pevné pásky krásné látky. Jak silný bude tento pás, pokud je známo, že Bob má 10 m² tkaniny.

Nechť pás má tloušťku x m, pak bude plocha tkaniny podél dlouhé strany pokrývky (5 + 2 * x) * x a vzhledem k tomu, že dlouhé strany jsou 2, máme: 2 * x * (5 + 2 * x). Na krátké straně bude plocha šitého materiálu 4 x, protože tyto strany jsou 2, dostaneme hodnotu 8 x. Všimněte si, že hodnota 2 * x byla přidána k dlouhé straně, protože délka přikrývky se zvýšila o toto číslo. Celková plocha textilie ušitá na přikrývku je 10 m². Proto získáme rovnost: 2 * x * (5 + 2 * x) + 8 * x = 10 => 4 * x² + 18 * x-10 = 0.

Pro tento příklad je diskriminant: D = 18²-4 * 4 * (- 10) = 484. Jeho kořen je 22. Pomocí vzorce získáme požadované kořeny: x = (-18 ± 22) / (2 * 4) 5, 0,5). Samozřejmě, ze dvou kořenů je pro stav problému vhodné pouze číslo 0,5.

Pás tkaniny, který si Bob vloží do deky, tak bude mít šířku 50 cm.