Rozdělit nulou. Fascinující matematika
Číslo 0 může být reprezentováno jako druh hranice oddělující svět reálných čísel od imaginárních nebo negativních. Vzhledem k nejednoznačné poloze mnoho operací s touto číselnou hodnotou nepodléhá matematické logice. Nemožnost dělení nulou je živým příkladem. A vyřešené aritmetické operace s nulou mohou být provedeny pomocí obecně přijatých definic.
Historie nuly
Zero je referenční bod ve všech standardních počítacích systémech. Evropané začali používat toto číslo poměrně nedávno, ale mudrci Starověká Indie používá nula za tisíc let, než bylo prázdné číslo pravidelně používáno evropskými matematiky. Dokonce před indiány byla nulová povinná množství v mayském číselném systému. Tento americký lid používal duodenální počet, a s nulou začali první den každého měsíce. Je zajímavé, že v květnu se znaménko označující "nulu" zcela shodovalo se znaménkem definujícím "nekonečno". Takto dávní Mayové dospěli k závěru, že tato množství jsou totožná a neznatelná. 
Matematické operace s nulou
Standardní matematické operace s nulou mohou být redukovány na několik pravidel.
Přidání: Pokud se libovolné číslo přidá nula, nezmění jeho hodnotu (0 + x = x).
Odčítání: při odečtení nuly od libovolného čísla zůstává hodnota odečtená nezměněna (x-0 = x).
Násobení: libovolné číslo vynásobené číslem 0 dává 0 v produktu (a * 0 = 0).
Oddělení: nula může být dělena libovolným číslem, které není rovno nule. V takovém případě bude hodnota takového zlomku 0. A rozdělení podle nuly je zakázáno. 
Exponentiace. Tato akce může být provedena libovolným číslem. Libovolné číslo zvýšené na stupeň nula dá 1 (x 0 = 1).
Zero je 0 až libovolný stupeň (0 a = 0).
V tomto případě okamžitě vzniká rozpor: výraz 0 0 nemá smysl.
Paradoxy matematiky
Skutečnost, že rozdělení na nulu je nemožné, mnoho lidí zná ze školy. Ale z nějakého důvodu není možné vysvětlit důvod takového zákazu. Ve skutečnosti, proč neexistuje vzorec pro dělení nulou, ale jiné akce s tímto číslem jsou celkem rozumné a možné? Odpověď na tuto otázku dávají matematici.
Ad
Věc je, že obvyklé aritmetické operace, které žáci studují na základní škole, jsou ve skutečnosti daleko od toho, aby se rovnali právům, jak se nám zdá. Všechny jednoduché operace s čísly lze snížit na dvě: doplnění a násobení. Tato opatření představují podstatu samotného pojetí čísla, zatímco zbývající operace jsou založeny na použití těchto dvou.
Přidání a násobení
Vezměte příklad standardního odečtu: 10-2 = 8. Ve škole se to považuje jednoduše: pokud jsou odebrány dva předměty z deseti položek, zůstane osm. Ale matematici se na tuto operaci dívají zcela jinak. Koneckonců taková operace jako odčítání pro ně neexistuje. Tento příklad lze zapsat jiným způsobem: x + 2 = 10. U matematiků je neznámý rozdíl jen číslo které je třeba přidat k dvěma, aby bylo osm. A zde není třeba odečítat, stačí najít příslušnou číselnou hodnotu.
Ad
Násobení a rozdělení jsou považovány za stejné. V příkladu 12: 4 = 3 lze rozumět, že jde o rozdělení osmi objektů na dvě stejné skupiny. Ale ve skutečnosti je to jen obrácený vzorec záznamu 3x4 = 12. Takové příklady rozdělení lze dát nekonečně. 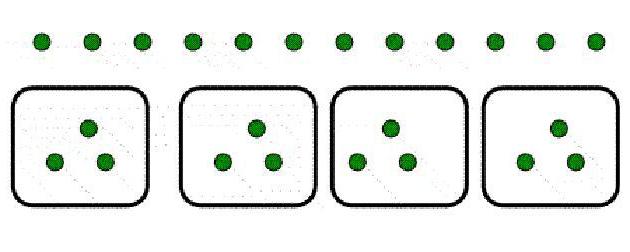
Příklady rozdělení o 0
Zde se stává trochu jasné proč není možné rozdělit nulou. Násobení a rozdělení podle nuly se řídí vlastními pravidly. Všechny příklady rozdělení tohoto množství lze formulovat jako 6: 0 = x. Ale toto je obrácený záznam výrazu 6 * x = 0. Ale, jak víte, libovolné číslo vynásobené číslem 0 udává v produktu pouze hodnotu 0. Tato vlastnost je vlastní samotné koncepci nulové hodnoty.
Ukazuje se, že neexistuje takové číslo, které by při násobení 0 dalo jakoukoliv hmotnou hodnotu, to znamená, že tento úkol nemá žádné řešení. Tato odpověď by se neměla bát, je to přirozená odpověď na úkoly tohoto typu. Jen psaní 6: 0 nemá smysl a nemůže nic vysvětlovat. Stručně řečeno, tento výraz lze vysvětlit velmi nesmrtelným "dělením nulou je nemožné".
Ad
Existuje operace 0: 0? Je-li násobení operací 0 legální, může být nula rozdělena nulou? Koneckonců, rovnice formuláře 0x 5 = 0 je naprosto legální. Namísto číslice 5 můžete zadat hodnotu 0, produkt se nezmění. 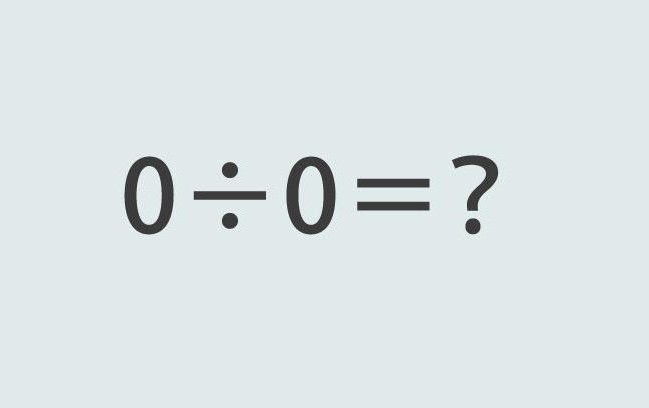
Opravdu 0x0 = 0. Ale je stále nemožné rozdělit na 0. Jak bylo uvedeno, dělení je prostě inverzní násobení. Takže pokud v příkladu 0x5 = 0, musíme určit druhý faktor, dostaneme 0x0 = 5. Nebo 10. Nebo nekonečno. Rozdělení nekonečna o nulu - jak se vám líbí?
Ale pokud nějaké číslo zapadá do výrazu, pak nemá smysl, nemůžeme si vybrat z nekonečné množiny čísel. A pokud ano, znamená to, že výraz 0: 0 nemá smysl. Ukazuje se, že ani samotná nula nemůže být dělena nulou.
Ad
Vyšší matematika
Rozdělení na nulu je bolest hlavy pro matematiku. Studoval na technických univerzitách matematická analýza mírně rozšiřuje koncept úkolů, které nemají řešení. Například k již známému výrazu 0: 0 přidávají se nové, které nemají řešení v matematických kurzech:
- nekonečno dělené nekonečno: ∞: ∞;
- nekonečno minus nekonečno: ∞ - ∞;
- jednotka zvýšená na nekonečný výkon: 1 ∞ ;
- nekonečno vynásobené 0: ∞ * 0;
- některé další.
Základní metody řešení těchto výrazů jsou nemožné. Ale vyšší matematika, díky dalším možnostem pro řadu podobných příkladů, poskytuje konečná řešení. To je zvláště patrné při zvažování problémů z teorie limitů.
Odhalení nejistoty
V teorii hranic je hodnota 0 nahrazena podmínkou nekonečně malou proměnnou. A výrazy, ve kterých je rozdělení nulou dosaženo nahrazením požadované hodnoty, se převádějí. Níže je standardní příklad zveřejnění limitu pomocí běžných algebraických transformací:

Jak je zřejmé z příkladu, jednoduché snížení frakce vede k jeho úplné racionální odpovědi.
Při zvažování hranic trigonometrických funkcí mají jejich výrazy tendenci být redukovány na první pozoruhodnou hranici. Při posuzování limitů, při kterých se jmenovatel při nastavování limitu změní na 0, použijte druhý pozoruhodný limit.
Metoda L'Hôpital
V některých případech mohou být limity výrazů nahrazeny limitem jejich derivátů. Guillaume Lopital - francouzský matematik, zakladatel francouzské matematické analýzy. Dokázal, že hranice výrazů se rovnají hranicím derivátů těchto výrazů. V matematickém psaní je jeho pravidlo následující. 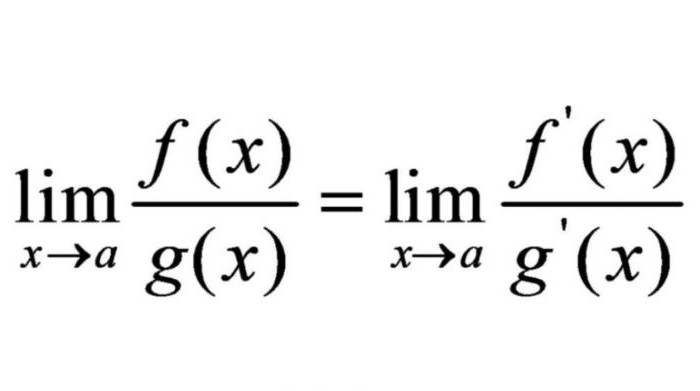
V současné době se metoda L'Hôpital úspěšně používá při řešení nejistot typu 0: 0 nebo ∞: ∞.