Extrémní funkční body. Jak najít?

Matematická analýza - je to spíše zábavná část matematiky, která se tváří absolutně všem absolventským třídám a studentům. Nicméně, ne každý má rád matan. Někteří možná nerozumí ani elementárním věcem, jako je zdánlivě standardní studie funkce. Tento článek je určen k opravě takové chyby. Chcete se dozvědět více o analýze funkce? Chtěli byste vědět, jaké jsou extrémní body a jak je najít? Tento článek je pro vás.

Studium funkčního grafu

Za prvé, stojí za pochopení, proč je nutné analyzovat graf vůbec. Existují jednoduché funkce kreslení, které nejsou obtížné. Parabola může sloužit jako živý příklad takové funkce. Nakreslit její rozvrh není těžké. Vše, co je zapotřebí, je najít čísla, pro něž má funkce za použití jednoduché transformace hodnotu. A v zásadě je to vše, co je nutné nakreslit, aby bylo možné kreslit graf paraboly.

Ale co když funkce, jejíž graf musíme čerpat, je mnohem obtížnější? Vzhledem k tomu, že vlastnosti složitých funkcí jsou poměrně obskurní, je nutné provést celou analýzu. Pouze tehdy může být funkce zobrazena graficky. Jak to udělat? Odpověď na tuto otázku naleznete v tomto článku.

Plán funkční analýzy

První věc, kterou je třeba udělat, je provést povrchní studium funkce, během níž najdeme doménu definice. Takže začneme v pořádku. Doména definice je sbírka hodnot, podle kterých je funkce určena. Jednoduše řečeno, toto jsou čísla, která mohou být použita ve funkci namísto x. Chcete-li určit rozsah, stačí se podívat na položku. Například je zřejmé, že funkce y (x) = x ³ + x ² - x + 43 domény definice je množina reálných čísel. No, s funkcí (x ² - 2x) / x, všechno je trochu jiné. Vzhledem k tomu, že číslo v jmenovateli nesmí být 0, bude v oblasti reálné funkce kromě nuly i reálná čísla.

Poté musíte nalézt tzv. Nulové funkce. Jedná se o hodnoty argumentu, pro který celá funkce přebírá hodnoty nula. K tomu je třeba rovno funkci nulu, podrobně ji zvážit a provést některé transformace. Využijte funkci y (x) = (x ² - 2x) / x, která je již známa. Z kurzu školy víme, že zlomek je 0, když je čitatel nula. Proto vyřadíme jmenovatele a začneme pracovat s čitatelem tak, že to rovná nule. Získáme x ² - 2x = 0 a vložíme x pro závorky. Proto x (x - 2) = 0. V důsledku toho zjistíme, že naše funkce je nula, když x se rovná 0 nebo 2.

Extrémní body na grafu funkcí

Během studia grafu funkce mnoho čelí problému ve formě extrémních bodů. A je to divné. Koneckonců, extrémy jsou poměrně jednoduché téma. Nevěříš? Ujistěte se, že jste si přečetli tuto část článku, v níž budeme hovořit o minimálních a maximálních bodech.

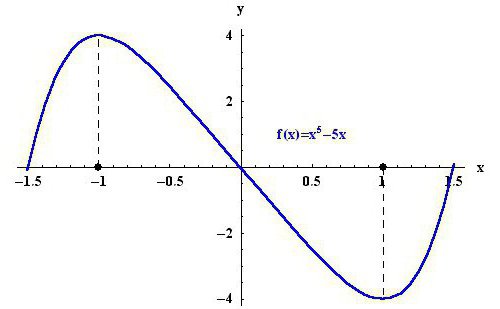
Začínat je pochopit, co představuje extrém. Extrém je mezní hodnota, kterou funkce na grafu dosáhne. Odtud se ukazuje, že existují dvě extrémní hodnoty - maximální a minimální. Pro přehlednost se můžete podívat na obrázek výše. Ve studované oblasti je bod -1 maximální z funkce y (x) = x ⁵ - 5x a bod 1 je minimální.

Také nezaměňujte koncepty. Extrémními body funkce jsou ty argumenty, při kterých daná funkce přebírá extrémní hodnoty. Na druhou stranu je extrémem hodnota minima a maxima funkce. Zvažte například obrázek výše. -1 a 1 jsou extrémní body funkce, a 4 a -4 jsou samotné extrémy.

Hledání extrémních bodů

Ale jak lze najít extrémní body funkce? Je to docela jednoduché. První věcí je najít derivát rovnice. Předpokládejme, že máme úkol: "Najděte extrémní body funkce y (x), x je argument. Pro zřetelnost použijeme funkci y (x) = x ³ + 2x ² + x + 54. Rozlišujme a dostáváme následující rovnici: 3x ² + 4x + 1. Nakonec jsme získali standard kvadratická rovnice. Vše, co je potřeba udělat, je nulovat a najít kořeny. Vzhledem k tomu, že diskriminant je větší než nula (D = 16 - 12 = 4), je tato rovnice definována dvěma kořeny. Najděte je a získáte dvě hodnoty: 1/3 a -1. To budou extrémní body funkce. Jak však určit, kdo je kdo? Který bod je maximální a co je minimum? Chcete-li to provést, vzít další bod a zjistit jeho hodnotu. Vezměte například číslo -2, které je vlevo od souřadné čáry od -1. Nahrazujeme tuto hodnotu do naší rovnice y (-2) = 12 - 8 + 1 = 5. V důsledku toho jsme získali kladné číslo. To znamená, že v intervalu od 1/3 do -1 se funkce zvyšuje. To naopak znamená, že v intervalech od mínus nekonečno k 1/3 a od -1 do plus nekonečna se funkce snižuje. Můžeme tedy konstatovat, že číslo 1/3 je minimálním bodem funkce na sledovaném intervalu a -1 je maximální bod.

Součet extrémních bodů funkce

Je také třeba poznamenat, že je nutné nejen najít extrémní body na USE, ale také provádět nějaký druh operace s nimi (přidávat, množit, atd.). Z tohoto důvodu je třeba věnovat zvláštní pozornost podmínkám problému. Koneckonců kvůli nepozornosti můžeš ztratit body.