Fibonacciho sekvence a principy Zlaté sekce
Fibonacciova sekvence, která se stala známou většinou prostřednictvím filmu a knihy Da Vinciho kódu, je řada čísel odvozených italským matematikem Leonardem z Pise, lépe známým pseudonymem Fibonacci, ve 13. století. Následovníci vědce si všimli, že vzorec, kterému tato řada čísel podléhá, najde jeho odraz ve světu kolem nás a rezonuje s jinými matematickými objevy, čímž nám otevře dveře tajemství vesmíru. V tomto článku budeme popisovat, jaká je sekvence Fibonacci, zvážit příklady mapování tohoto vzoru v přírodě a také jej porovnat s jinými matematickými teoriemi. 
Formulace a definice
Série Fibonacci je matematická sekvence, jejíž každý prvek se rovná součtu předchozích dvou. Nechte některého člena posloupnosti xn. Získáme tedy vzorec platný pro celou řadu: xn + 2 = xn + xn + 1. S tímhle pořadí sekvencí bude vypadat takto: 1, 1, 2, 3, 5, 8, 13, 21, 34. Další číslo bude 55, protože součet 21 a 34 je 55. A tak dále podle stejného principu.
Ad
Příklady v prostředí
Pokud se podíváme na rostlinu, zejména na korunu listů, poznamenáváme, že kvete ve spirále. Úhly se tvoří mezi sousedními listy, které zase tvoří správnou matematickou sekvenci Fibonacci. Díky této funkci každý list, který roste na stromu, přijímá maximální množství slunečního světla a tepla. 
Fibonacci Math Puzzle
Slavný matematik představil svou teorii jako hádanku. Zní to takto. Můžete dát pár králíků v uzavřeném prostoru, abyste zjistili, kolik pár králíků se narodí do jednoho roku. Vzhledem k povaze těchto zvířat je skutečnost, že každý měsíc je pár schopen produkovat nový pár a jsou připraveni chovat po dosažení dvou měsíců, nakonec obdržel slavný počet čísel: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144 - kde je zobrazen počet nových párů králíků v každém měsíci.
Ad
Fibonacci sekvence a proporcionální poměr
Tato série má několik matematických nuancí, které určitě musíte zvážit. On, blížící se pomalejším a pomalejším (asymptotickým), má tendenci k nějakému poměrnému poměru. Ale je to nerozumné. Jinými slovy, je číslo s nepředvídatelnou a nekonečnou sekvencí desetinných čísel ve zlomkové části. Například poměr jakéhokoli prvku série se liší kolem čísla 1.618, pak překročí a poté dosáhne. Následujícími analogickými přístupy se používá 0.618. Co je nepřímo úměrné číslu 1.618. Pokud rozdělíme elementy prostřednictvím jednoho, dostaneme 2.618 a 0.382. Jak jste již pochopili, jsou také nepřímo úměrní. Výsledná čísla se nazývají Fibonacci koeficienty. A teď budeme vysvětlovat, proč jsme provedli tyto výpočty. 
Zlatý poměr
Rozlišujeme všechny objekty kolem nás podle určitých kritérií. Jedna z nich je forma. Někteří z nás přitahují více, některé méně a někteří se jim nelíbí. Je poznamenáno, že symetrický a proporcionální objekt je mnohem jednodušší vnímán člověkem a způsobuje pocit harmonie a krásy. Celý obraz vždy obsahuje části různých velikostí, které jsou v určitém poměru mezi sebou. Odpověď na otázku, co se nazývá Zlatá sekce. Tento koncept znamená dokonalost vztahu mezi celkem a částmi v přírodě, věda, umění a atd. Z matematického hlediska zvažte následující příklad. Vezměte segment libovolné délky a rozdělte ji na dvě části, takže menší část se vztahuje k větší části jako součet (délka celého segmentu) k většímu. Takže vezmeme segment c pro hodnotu jednoho. Jeho část a bude rovna 0,618, druhá část b , se ukáže, se rovná 0,382. Proto dodržujeme podmínku Golden Section. Poměr segmentu c k a se rovná 1,618. A poměr částí c a b je 2.618. Získali jsme koeficienty Fibonacci, které jsou již známy. Stejným principem jsou postaveny zlatý trojúhelník, zlatý obdélník a zlatý kvádr. Je také třeba poznamenat, že poměrný poměr částí lidského těla se blíží Zlatému poměru. 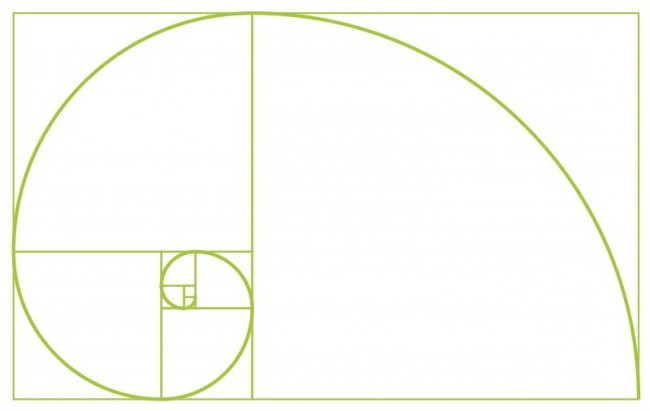
Je Fibonacci sekvence základem všeho?
Pokusíme se spojit teorii Zlaté sekce a slavné série italských matematiků. Začněme dvěma čtvercami první velikosti. Potom nahoře přidáme další čtverec druhé velikosti. Přibližme stejnou číslici s délkou strany rovnající se součtu obou předchozích stran. Podobně nakreslete čtverec páté velikosti. A tak můžete pokračovat neurčitě, dokud se nudíte. Hlavní věc je, že velikost strany každého následujícího čtverce se rovná součtu hodnot stran obou předešlých. Získáme sérii polygonů, jejichž délka je Čísla Fibonacci. Tyto číslice se nazývají Fibonacci obdélníky. Zkrojme hladkou čáru v rozích našich polygonů a získáme ... špirálu Archimedes! Zvýšení výšky této postavy, jak víte, je vždy jednotné. Pokud zapnete fantasy, výsledný obrázek může být spojen se skořápkou. Z toho můžeme usoudit, že sekvence Fibonacci je základem proporcionálních, harmonických poměrů prvků v okolním světě. 
Matematická sekvence a vesmír
Pokud se podíváte pozorněji, pak spirála Archimedes (někde explicitně, ale někde zakrytá) a proto princip Fibonacci lze vysledovat v mnoha z obvyklých přírodních prvků, které obklopují člověka. Například, stejné mušle shell, brokolice florets, slunečnice květ, kužel jehličnatých rostlin a podobně. Pokud se podíváme pryč, uvidíme sekvenci Fibonacci v nekonečných galaxiích. Dokonce i osoba, která je inspirována přírodou a přijímá její podobu, vytváří objekty, ve kterých lze vysledovat výše uvedené série. Teď je čas si vzpomenout na Zlatou sekci. Spolu s Fibonacciovým vzorem jsou sledovány principy této teorie. Existuje verze, že sekvence Fibonacciho je druhovým přírodním testem, který se přizpůsobuje dokonalé a základní logaritmické sekvenci Zlaté sekce, která je téměř totožná, ale nemá žádný začátek a je nekonečná. Povaha přírody je taková, že musí mít svůj vlastní výchozí bod, z něhož se staví na vytvoření něčeho nového. Vztah prvních prvků řady Fibonacci je daleko od zásad Zlaté sekce. Nicméně, čím dál pokračujeme, tím více se tento rozdíl vyrovnává. K určení sekvence je nutné znát její tři prvky, které následují navzájem. Pro zlatou posloupnost stačí dvě. Vzhledem k tomu, že je jak aritmetický, tak i geometrická progrese.
Závěr
Přesto, na základě výše uvedených skutečností, můžete se zeptat zcela logických otázek: "Odkud pocházejí tyto čísla?" Kdo je autorem celého světa, který se ho snažil udělat dokonalým? Bylo to vždycky tak, jak to chtěl, a pokud ano, proč to selhalo? Co se stane dál? " Při hledání odpovědi na jednu otázku získáte další. Vyřešil jsem to - další dva se objevují. Když je vyřešíte, dostanete ještě tři. Po vyřešení těchto problémů obdržíte pět nevyřešených. Pak osm, pak třináct, dvacet jedna, třicet čtyři, padesát pět ...