Teorie grafů: Základní definice

Teorie grafů je obor matematiky používaný v informatice a programování, ekonomie, logistika a chemie.

Co je graf

Grafické systémy se často používají k popisu struktury systémů. Prvky v nich jsou reprezentovány kruhy, tečkami, čtvercemi atd. A spojení mezi prvky jsou čáry nebo šipky. Současně není důležité ani to, jak jsou zobrazeny prvky, ani délka nebo tvar řádků - pouze ty prvky, které jsou spojeny. Takže graf je dvojice tvarů (A, M), kde A je konečná množina vrcholů a M je množina hran - čáry spojující některé vrcholy.

Základní pojmy teorie grafů

Pro orientační graf nebo digraph (viz obrázek níže) jsou okraje orientovány, nazvané oblouky a jsou reprezentovány šipkami. Oblouk může být označen uspořádaným dvojicí vrcholů, které se připojí - počáteční a konečný.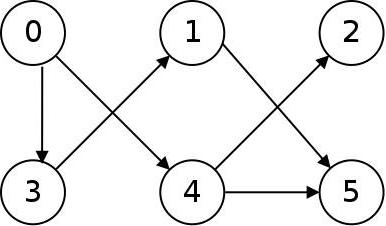

Pro neorientovaný graf (viz obrázek níže) jsou hrany reprezentovány přímkami bez orientace. Proto je dvojice vrcholů, které spojuje okraj, neuspořádaná. Oba tyto vrcholy jsou konce hrany.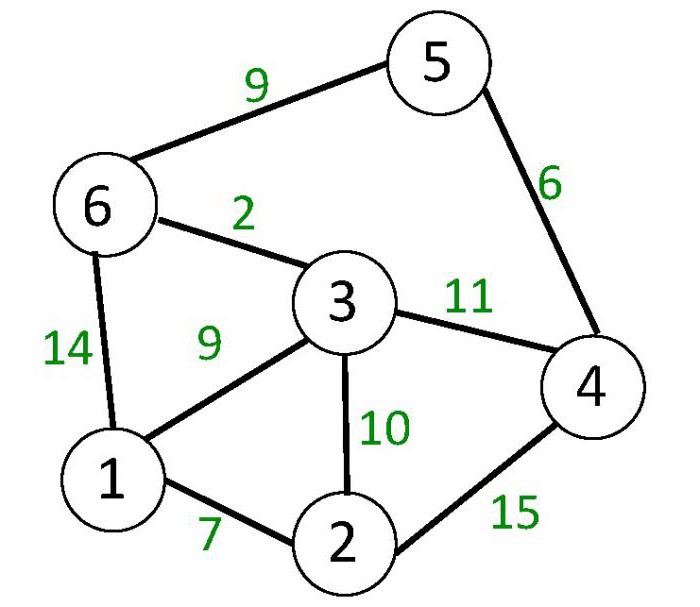

Pokud vrcholy a a b jsou konce hrany (nebo začátek a konec oblouku) grafu, pak říkáme, že vrcholy a a b jsou dopadající na tuto hranu (oblouk), také okraj (oblouk) je doprovázen vrcholy a a b. Pokud jsou vrcholy a a b konce hrany, pak se (a a b) nazývají vedle sebe.

Nejčastěji jsou grafy, jejichž okraje jsou stejného typu - orientované či nikoliv.

Pokud mají hrany stejný začátek a konec, pak se nazývají více okrajů a graf, ve kterém se nacházejí, se nazývá vícestránkový graf.

Teorie grafů také používá pojem "smyčka" - hranice, která jde a nastavuje na stejném vrcholu. Graf, ve kterém jsou smyčky, se nazývá pseudograf.

Nejběžnější neorientované grafy, které nemají více okrajů a žádné smyčky. Tyto grafy se nazývají obyčejné. Nemají více okrajů, takže můžete určit hranu a odpovídající pár vrcholů.

Každý vrchol digraphu je charakterizován:

• Nedostatky. To je počet oblouků, které z něj vycházejí.
• Nedostatky. Toto je počet oblouků, které se dostanou do daného vrcholu.

Součet polovičních stupňů vstupu digraphu a součtu polovičních stupňů výsledku se rovná celkovému počtu oblouků grafu.

V neorientovaném grafu je každý vrchol charakterizován stupněm jeho vrcholu. To je počet okrajů, které jsou v horní části. Celkový součet stupňů vrcholů grafu je počet okrajů vynásobený dvěma: každý okraj poskytne příspěvek, který se rovná dvěma.

Vrchol se stupněm 0 se nazývá izolovaný.

Závěsný vrchol je vrchol se stupněm 1.

Teorie grafů nazývá prázdný graf, ve kterém neexistuje jediný okraj. Kompletní graf je obyčejný graf, ve kterém jsou 2 vrcholy vedle sebe.

Vážené grafy jsou grafy, na které jsou okamžitě vyneseny vrcholy nebo okraje (oblouky) nebo i vrcholy a okraje (oblouky), jsou přiřazena některá čísla. Jsou nazývány závaží. Druhý obrázek zobrazuje neorientovaný graf, jehož hrany jsou váženy.

Počítá se: isomorfismus

Koncept isomorfismu se používá v matematice. Zejména teorie grafů ji definuje následovně: dva grafy U a V jsou izomorfní, jestliže mezi těmito množinami jejich vrcholů v těchto grafech existuje bijekce: každé 2 vrcholy v grafu U jsou spojeny okrajem, pokud a pouze pokud je stejné v grafu V vrcholy (které mohou být volány jinak). Níže uvedený obrázek ukazuje dva izomorfní grafy, ve kterých mezi vrcholy namalovanými ve stejných barvách v prvním i druhém grafu je výše popsaná bijekce.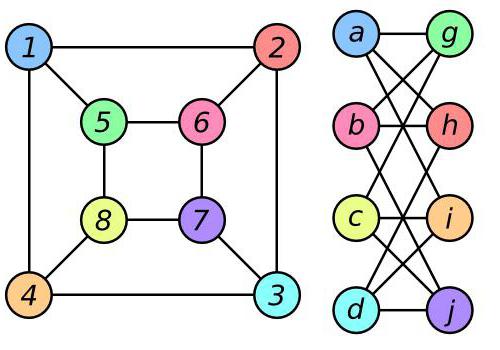

Cesta a cykly

Cesta v neorientovaném nebo orientovaném grafu je posloupnost okrajů, kde každá další začíná na vrcholu, ve kterém končí předchozí. Jednoduchá cesta je cesta, ve které jsou všechny vrcholy, s výjimkou pravděpodobně počáteční a konečné, a hrany jsou různé. Cyklus v digraphu je cesta, jejíž počáteční a konečné vrcholy se shodují a zahrnují alespoň jednu hranu. Cyklus v nerovnoměrném grafu je cesta, která obsahuje nejméně tři různé hrany. V druhém obrázku je cyklus například cesta (3, 1), (6, 3), (1, 6).

Teorie grafů v programování se používá k sestavení grafových schémat algoritmů.