Vyšší matematika: letadlo ve vesmíru

Druhý po přímce je důležitým prvkem prostorové geometrie rovina. Schopnost jej popsat rovnicí umožňuje vypočítat prostorové úhly a výšky pro různé trojrozměrné tvary. V tomto článku uvádíme všechny rovnice, které popisují planetu v prostoru. Zvažte také možné varianty vzájemného uspořádání letadel.

Geometrická koncepce roviny

V dvojrozměrné geometrii není rovina zvažována, protože všechny problémy jsou řešeny pouze v souřadnicích x a y. Když přidáme třetí osu souřadnic z, rovina se stane důležitým geometrickým prvkem.

Pojem "rovina" se chápe jako sbírka bodů, z nichž každá dvě, pokud je spojena, bude výsledný vektor vždy kolmý na nějaký daný vektor. Tento daný vektor se nazývá normální. Normální hraje důležitou roli v číselném popisu roviny a její vlastnosti se používají k řešení různých problémů.

Na obrázku níže jsou tři roviny v prostoru (modré), které protíná čtvrtý (červený).

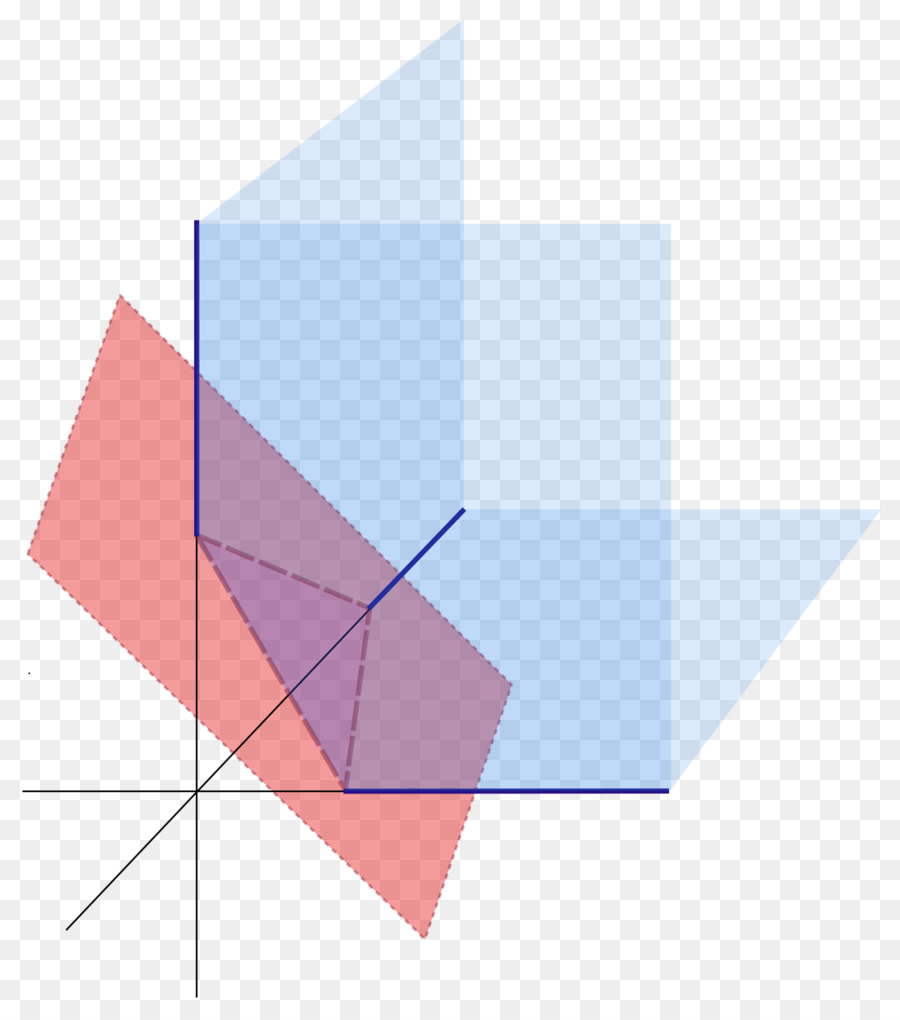
Obecná rovnice

Výše uvedená definice pomůže získat rovnici pro rovinu ve vesmíru v souřadnicích. Předpokládejme, že existuje nějaký bod se známými souřadnicemi Q (x ₀ ; y ₀ ; z ₀ ). Je známo, že leží v určité rovině, jejíž normál se rovná n (A; B; C). Předpokládejme nyní, že k této rovině patří i libovolný bod M (x; y; z). Ta druhá znamená, že vektory QM¯ a n¯ budou kolmé, to znamená, že jejich skalární produkt zmizí. Proto můžeme napsat následující rovnost:

(QM * * n¯) = 0.

Nahrazením souřadnic do ní a otevřením konzolí se dostáváme k rovnici:

(xx ₀ ) * A + (yy ₀ ) * B + (zz ₀ ) * C = 0 =>

A * x + B * y + C * z + D = 0, kde D = -1 * (A * x ₀ + B * y ₀ + C * z ₀ ).

Výsledná rovnice pro rovinu se nazývá obecná. Má stejnou formu jako obecná rovnice pro přímou rovnici v rovině. Je zřejmé, že koeficienty směřující k proměnným x, y a z nejsou nic víc než souřadnice kolmé roviny vektoru. Říká se mu režie.

Všimněte si, že pokud při získání obecné rovnice není specifický bod Q neznámý a existuje pouze směrový vektor n, pak dosáheme rovnice pro množinu rovnoběžných rovin, která se liší pouze parametrem D.

Částečná rovnice

Při zobrazení rovin v prostoru, pokud jsou uvedeny konkrétní osy souřadnic, je nejjednodušší udržovat geometrické konstrukce, pokud jsou body, kde rovina protíná tyto osy. Výraz, který umožňuje zjistit hodnoty souřadnic průsečíku roviny s osami x, y a z, se nazývá intervalová rovnice. Může být získán provedením některých matematických transformací s obecnou rovnicí.

Předpokládejme, že je známa následující rovnice:

A * x + B * y + C * z + D = 0.

Přeneste volnou tečku D na pravou stranu rovnice a pak obě strany rovnice rozdělte tak, aby jednotka byla vpravo. Máme:

A * x + B * y + C * z = -D =>

x / (- D / A) + y / (- D / B) + z / (- D / C) = 1 nebo

x / p + y / q + z / r = 1, kde p = -D / A, q = -D / B, r = -D / C

Výsledný výraz se v segmentu nazývá rovnicí a délky segmentů, které jsou odříznuty na osách x, y a z, začínají od bodu (0; 0; 0), mají hodnoty p, q a r. To lze zkontrolovat následujícím způsobem: pokud předpokládáme, že souřadnice podél osy y a z jsou nula, pak x je rovno q. To znamená, že průsečík s osou x má souřadnice (p; 0; 0). Podobně, argumentujeme, získáme zbývající dvě souřadnice (0; q; 0) a (0; 0; r).

Parametrická vektorová rovnice

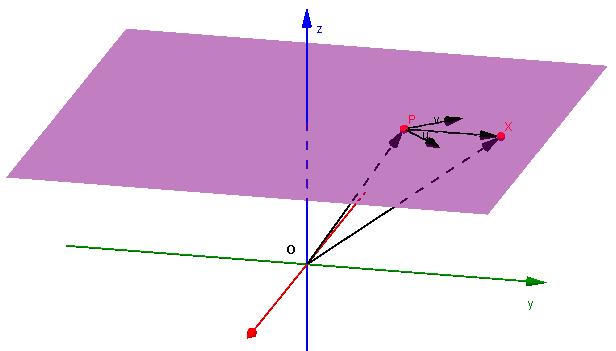
Toto je třetí důležitý typ rovnice, který se často používá při řešení problémů. Bylo ukázáno výše, že rovina je jednoznačně definována bodem a normálním vektorem. Je však možné tento geometrický dvourozměrný objekt určit jiným způsobem.

Předpokládejme, že existují dva koplanární vektory, které nejsou navzájem rovnoběžné. Označujeme je pomocí u (a ₁ ; b ₁ ; c ₁ ) a v¯ (a ₂ ; b ₂ ; c ₂ ). Je také známý bod Q (x ₀ ; y ₀ ; z ₀ ). Jaká bude rovnice roviny, která prochází tímto bodem a dva vektory?

Na tuto otázku můžete odpovědět tím, že získáte rovnici obecně. Tento problém však řešíme jiným způsobem. Připomeňme, že každý vektor roviny může být rozložen do dvou dalších koplanárních vektorů, které také patří do této roviny. To znamená, že libovolný vektor QP ¯, kde P (x; y; z) může být reprezentován jako:

QP ¯ = α * u¯ + β * v¯.

Během všech bodů P roviny získáme příslušné parametry α a β. Rovnice daná pro rovinu se nazývá parametrický vektor. Často se zaznamenává ve formě souřadnic:

(x, y; z) = (x ₀ ; y ₀ ; z ₀ ) + α * (a ₁ ; b ₁ ; c ₁ ) + β * (a ₂ ; b ₂ ; c ₂ ).

Je vidět, že tato forma psaní roviny je podobná vektorové rovnici pro přímku v dvourozměrných a trojrozměrných případech.

Tento výraz lze také psát explicitněji oddělením proměnných:

x = x ₀ + α * a ₁ + β * a ₂ ;

y = y ₀ + α * b ₁ + β * b ₂ ;

z = z ₀ + α * c ₁ + β * c ₂ .

Tyto tři rovnice mají tvar podobný parametrické rovnici pro přímku ve vesmíru. Tento typ se často používá při přeměně vektorové rovnice na běžnou rovinu.

Paralelní roviny

Existují pouze dvě možnosti relativní polohy dvou rovin ve vesmíru. V této části článku dáváme podmínku, když jsou paralelní.

Pokud jsou obě rovnice roviny uvedeny v obecné podobě, je jejich paralelní poměrně jednoduchá. Dvě roviny budou rovnoběžné, pokud jsou jejich vektory takovými průvodci. Předpokládejme, že existují dvě rovnice:

A * x + B ₁ * y + C ₁ * z + D ₁ = 0;

A ₂ x + B ₂ * y + C ₂ * z + D ₂ = 0.

Kolmo na každou rovinu vektoru jsou souřadnice:

n ₁ (A ₁ , B ₁ , C ₁ );

n ₂ (A ₂ , B ₂ , C ₂ ).

Jestliže vektor n ₁ ¯ může být reprezentován jako násobení reálným počtem vektoru n ₂ ¯, pak oba budou paralelní, to znamená:

n ₂ ¯ = l * n ₁ ¯, kde l je reálné číslo.

Dalším způsobem, jak určit jejich paralelismus, je najít kosinus úhlu mezi nimi skalárním produktem a moduly vektorů. Tento kosinus by se měl rovnat jednotce, pak budou vektory (roviny) paralelní. Odpovídající vzorec je:

cos (φ) = | (n ₁ ¯ * n ₂ ¯) | / (| n ₁ ¯ | * | n ₂ ¯ |) = 1.

Jsou-li rovnice rovin udávány v parametrické vektorové podobě, rovnoběžnost v prostoru rovin je také určena z stavu rovnoběžnosti normálů k nim. Abychom nalezli směrové vektory těchto normálů, měli bychom vzít vektorové produkty vektorů tvořících každou rovinu.

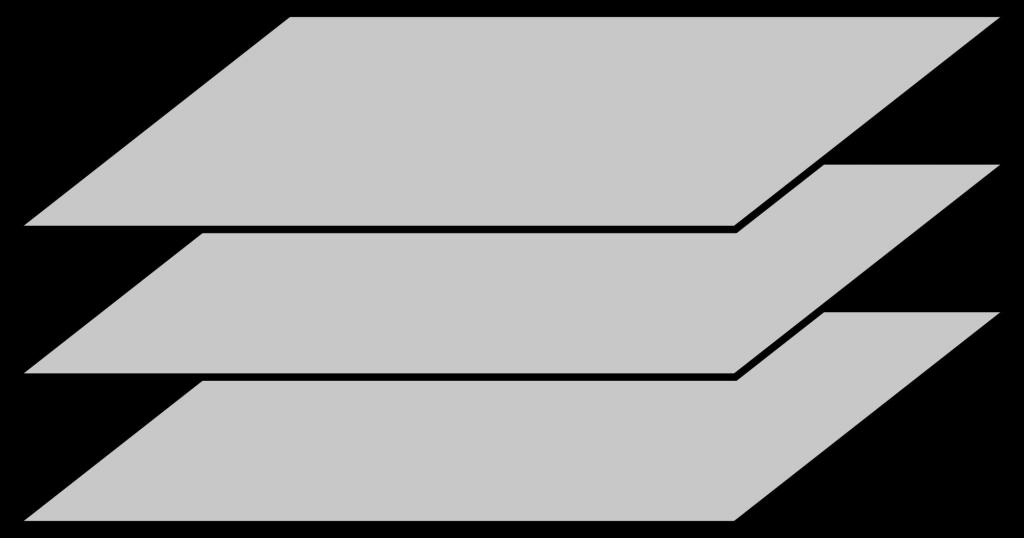
Obrázek výše ukazuje tři roviny, které jsou navzájem rovnoběžné.

Průsečík rovin

Toto je druhá verze vzájemného uspořádání v prostoru letadel. V tomto případě se obě letadla protínají podél přímky, která jim patří. V tomto případě je důležité, aby bylo možné vypočítat dihedral hrany tohoto křižovatka. Vždy se rovná úhlu mezi odpovídajícími vodícími vektory, tj. Mezi svislými rovinami rovin.

V předchozím odstavci již byl daný vzorec, který umožňuje výpočet úhlu mezi normály. Zde jej otevíráme pouze psaním souřadnic vektorů n ₁ ¯ a n ₂ ¯:

φ = arkcos (| A ₁ * A ₂ + B ₁ * B ₂ + C ₁ * C ₂ | / (√ (A ₁ ² + B ₁ ² + C ₁ ² ) C ₂ ² ))).

Tento vzorec je často používán při výpočtu dvojitých úhlů mezi rovinami pyramidy nebo šikmým hranolem.

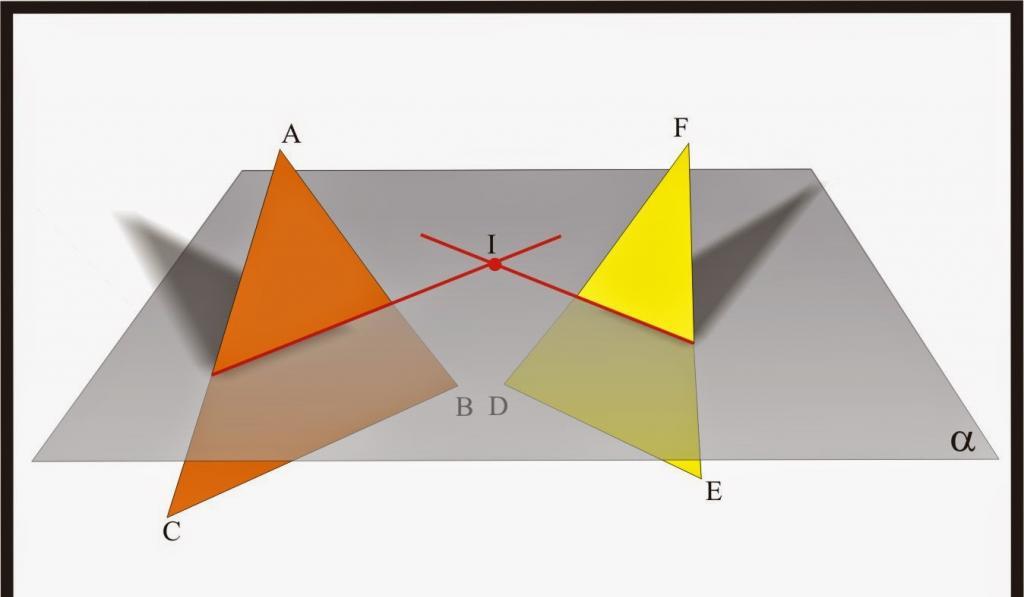
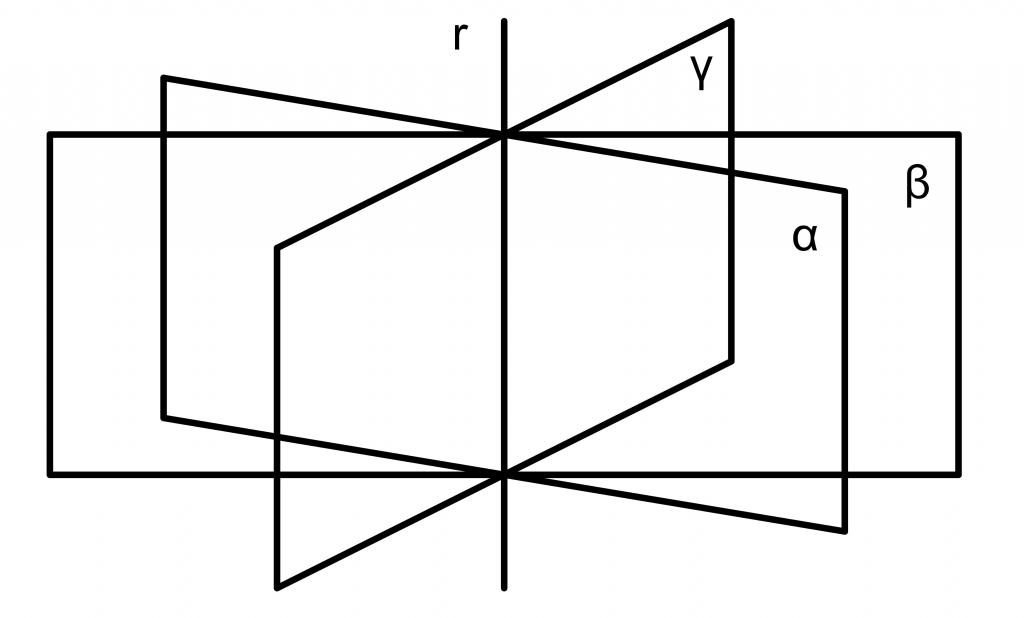
Dvě roviny, které protínají třetí horizontální rovinu, jsou znázorněny na obrázku výše.

Zvláštní případ průsečíku dvou rovin je úhel φ = 90 ^° , to znamená, že existuje kolmice uvažovaných geometrických objektů. Pro určení kolmosti není nutné vypočítat úhel φ za použití poněkud těžkopádného vzorce výše, pro to stačí vypočítat hodnotu skalárního produktu n ₁ a n ₂ ¯. Pro kolmé roviny je nula, to znamená:

(n ₁ ¯ * n ₂ ¯) = A ₁ * A ₂ + B ₁ * B ₂ + C ₁ * C ₂ = 0.

Svazek letadel

Pokud se protínají dvě roviny, všechny jejich společné body leží na jedné přímce. Mějte na paměti, že jednou z metod určení přímky ve vesmíru je systém dvou obecných rovnic roviny. Kolik letounů ve vesmíru lze přetáhnout přes jednu přímku? Nekonečné číslo. Jejich sbírka se nazývá balíček. Rovnice popisující tento svazek má následující podobu:

k ₁ * (A ₁ * x + B ₁ * y + C ₁ * z + D ₁ ) + k ₂ * (A ₂ * x + B ₂ * y + C ₂ * z + D ₂ ) = 0.

Zde k ₁ a k ₂ jsou libovolná čísla. Zvláštním případem je situace, kdy jeden nebo oba parametry k nemohou mít hodnotu nula. Předpokládejme, že k ₁ ≠ 0, pak rovnice trámu může být přepsána ve tvaru:

(A * x + B ₁ * y + C ₁ * z + D ₁ ) + k ₂ / k ₁ * (A ₂ * x + B ₂ * y + C ₂ * z + D ₂ ) = 0.

Tato rovnost popisuje všechny roviny paprsku s výjimkou přímky vektoru n ₂ ¯ (A ₂ , B ₂ , C ₂ ).

Příkladem svazku letadel je sbírka listů otevřené knihy.

Dále řešíme několik geometrických problémů aplikací získaných poznatků o vlastnostech letadel v prostoru.

Převést parametrickou vektorovou rovnici na obecnou

Vzhledem k následující rovinné rovnici v parametrické formě vektoru:

(x, y, z) = (1, 2, 0) + α * (1; 2; 3) + β * (- 1; 3; 0).

Je nutné ji napsat jako obecnou rovnici roviny ve vesmíru.

Pojďme to explicitně přepisovat:

x = 1 + α - β;

y = 2 + 2 * α + 3 * β;

z = 3 * α.

Z posledního výrazu získáme α, pak ho nahrazujeme první rovnicí a vyjádíme β. Nalezené parametry jsou nahrazeny do druhé rovnice, máme:

a = z / 3;

β = 1 - x + z / 3;

y = 2 + 2 * z / 3 + 3 - 3 * x + z =>

y + 3 * x + 5/3 * z - 5 = 0 =>

9 * x + 3 * y + 5 * z -15 = 0.

Abychom získali obecnou rovnici z parametrického vektoru, musíme nejprve explicitně napsat a pak vyjádřit parametry z hlediska souřadnic proměnných.

Převedení obecné do rovnice parametrického vektoru

Tento úkol je úplně opačný než předchozí. Zvažte techniky k jeho vyřešení.

Vzhledem k následující rovnici:

x-2 * y + 3 * z-1 = 0.

Za prvé, jedna souřadnice by měla být vyjádřena ve dvou. Express například x:

x = 2 * y-3 * z +1.

To znamená, že jakýkoli bod se souřadnicemi bude patřit rovině:

(2 * y-3 * z +1; y; z).

Teď tuto souřadnici přepsáme jako součet tří vektorů, první bude obsahovat pouze proměnnou y, druhou pouze z, a třetí bude sestávat pouze z čísel. Máme:

(x, y; z) = (2 * y; y; 0) + (-3 * z; 0; z) + (1; 0;

Je vidět, že otevřením této rovnice získáme obecné souřadnice pro bod roviny. Nyní zůstává jen vyčíslit proměnné v prvním a druhém vektoru a předefinovat je s parametry α a β. Máme:

(x; y; z) = (1; 0; 0) + α * (2; 1; 0) + β * (- 3; 0;

Získali jsme rovnici ve formě parametrického vektoru, podobně jako původní.

Obrázek roviny v souřadnicovém systému

Úloha je následující: podle známé rovnice by člověk měl kreslit rovinu ve vesmíru. Odpovídající rovnice je:

3 * x - y - 4 * z + 5 = 0.

K zobrazení této roviny je nutné nalézt body, na kterých protíná souřadné osy. Chcete-li to provést, můžete získat odpovídající rovnici v segmentu. V tomto případě však postupujeme jinak: dvě souřadnice se rovnají nule a vypočítáme třetí. Máme:

y = 0; z = 0; x = -5 / 3;

x = 0; z = 0; y = 5;

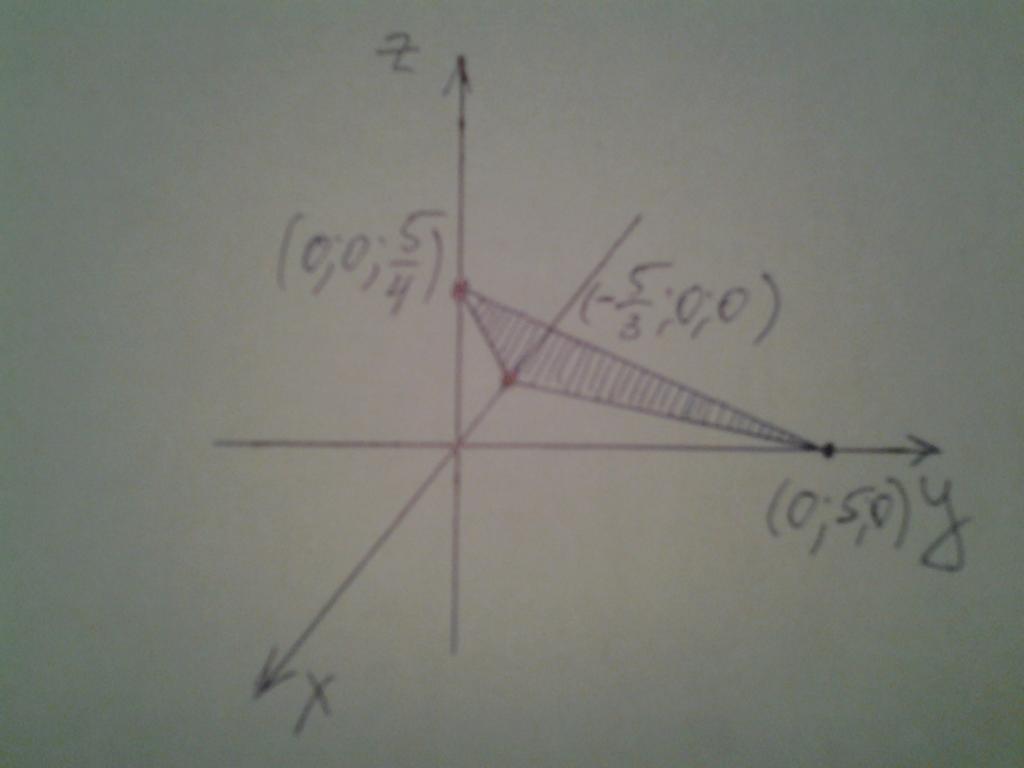
x = 0; y = 0; z = 5/4.

Zbývá položit získané body na souřadnicové osy a nakreslit rovinu mezi nimi. Pozice roviny v prostoru je znázorněna na obrázku níže.

Tři body a letadlo

Nechte dát tři body ve vesmíru:

M (1; -1; 3);

N (3; 2; -4);

L (2; 5; 0).

Je nutné najít letadlo, které prochází.

Z geometrie je známo, že tři body, které neleží na jedné přímce, jednoznačně určují rovinu. Jeho rovnice může být složena, pokud najdeme její vektorové vedení n. Bude rovno vektorovému produktu koplanárních vektorů ležících v rovině. Souřadnice vektorů lze získat ze souřadnic bodů, například:

MN ¯ (2; 3; -7);

ML¯ (1; 6; -3).

Jejich vektorový produkt dá vektoru n¯. Vypočítáme to takto:

n (33; -1, 9).

Vezmeme-li například bod M, získáme obecnou rovnici ve formě:

33 * x-y + 9 * z-61 = 0.

Souřadnice bodů N a L můžete nahradit rovnicí a ujistit se, že rovnost platí.