Jak vypočítat úhly mezi čárou a rovinou?

Při studiu geometrie školy ve dvourozměrném prostoru je věnována velká pozornost chování přímých linek. Když se obrátí na studium stereometrie v horních stupních, objeví se témata témat rovin a přímých linií ve vesmíru. Tento článek se zabývá jednou z těchto otázek. Tématem výpočtu mezi rovinami a pravými úhly a vzdálenostmi.

Rovná čára v rovině a způsoby jejího nastavení

Aby bylo možné úspěšně řešit výpočetní problémy mezi rovnými čarami a rovinami úhlů a vzdáleností, je nutné se naučit, jak matematicky nastavit tyto geometrické objekty, stejně jako ovládat metody práce s odpovídajícími rovnicemi. Začneme zadáním řádků v rovině.

Každý student zná následující vzorec:

y = k * x + b

Práce s ním je v dvojrozměrném prostoru velmi výhodná. Je snadné použít k vytvoření přímky v pravoúhlém souřadném systému. Kromě toho znalost koeficientu k pro každý z nich nám dovoluje říct, zda budou paralelní nebo zda se protínají (pro paralelní jsou jejich koeficienty k stejné).

Pokud napíšeme daný výraz v trochu jiné formě, získáme vzorec obecného typu pro přímku. Její forma je následující:

A * x + B * y + C = 0

Je zřejmé, že pomocí jednoduchých transformací získáte od ní první výraz.

Písmenné vzorce lze také použít k výpočtu úhlu průsečíku přímky. To však vyžaduje řadu transformací, což je nepohodlné. Proto když úloha vyžaduje nalezení úhlu, je vhodné použít vektorovou podobu reprezentace řádku. Její pohled může být napsán jako:

(x, y) = (x ₀ ; y ₀ ) + λ * (a; b)

V této rovnováze souřadnice X a Y s indexy nuly popisují polohu určitého bodu, kterým linka prochází. Hodnoty a a b jsou souřadnice vektoru ležícího na něm. Může být nasměrován jak v jednom směru, tak v přímém směru, přímka se nemění. Tento vektor se nazývá vodící vektor, protože jednoznačně určuje rozložení přímky v rovině. Lambda λ je parametr, který vezme libovolnou hodnotu ze sady reálných čísel.

Všimneme si, že vektorová podoba záznamu je pozoruhodná, která zřetelně obsahuje přímý úsek přímky, jejíž souřadnice se používají k určení úhlu mezi dvěma přímkami v rovině.

Rovná čára v trojrozměrném prostoru

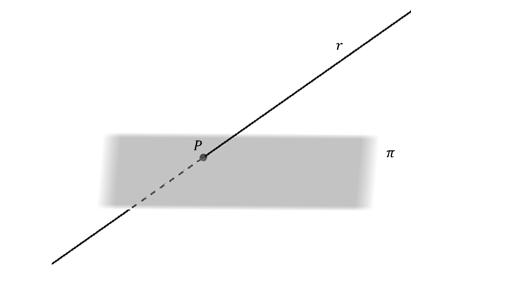
V prostoru popsaném třemi souřadnicovými osami je přímka definována v obecné podobě jako průsečík rovin. Zde, vzhledem k tématu článku, zvažujeme pouze vektorovou rovnici. Je to podobné jako u plochého případu, ale s přidáním třetí souřadnice:

(x, y; z) = (x ₀ ; y ₀ ; z ₀ ) + λ * (a; b; c)

Při řešení problémů je tento výraz vhodný pro otevření a použití v parametrické podobě:

x = x ₀ + λ * a;

y = y0 + λ * b;

z = z ₀ + λ * c

Všimněte si, že hodnota parametru λ, byť libovolná, závisí na všech třech rovnostech.

Popis letadla

Stejně jako pro přímku, pro letadlo existuje i řada způsobů, jak ji definovat. Zvažte pouze dvě z nich, které je důležité znát, abyste mohli v praxi řešit problémy.

První metodou zadání je přinést rovnici obecného typu. Je podobný odpovídajícímu výrazu pro přímku v dvojrozměrném případě:

A * x + B * y + C * z + D = 0

Kombinace prvních tří koeficientů je souřadnice vektoru směru pro tuto rovinu. Zpravidla se označuje symbolem n, to znamená:

n¯ = (A, B, C)

Čtvrtý koeficient D určuje vzdálenost mezi rovnoběžnými rovinami majícími první tři identické koeficienty.

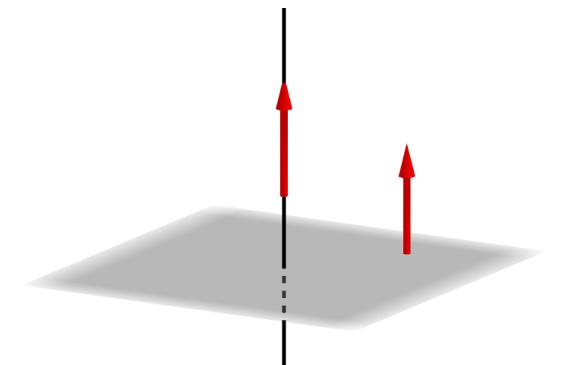
Vzhledem k tomu, že vektor n¯ leží na normální rovině, je kolmý na absolutně jakýkoliv vektor a přímku vytvořenou na jeho libovolných dvou bodech. Poznání souřadnic n¯ je klíčem při určování mezi přímkami a úhly úhlů.

Druhým způsobem definování roviny je vektor-parametrická forma rovnice. Je napsáno takto:

(x, y, z) = (x ₀ , y ₀ , z ₀ ) + λ * (a ₁ , b ₁ , c ₁ ) + γ * (a ₂ , b ₂ ;

Tato rovnost odráží skutečnost, že dvě přímky jednoznačně definují rovinu ve vesmíru. Druhý a třetí výraz označují dva směrové vektory pro libovolné přímé linie patřící rovině.

Normální vektor n¯ není explicitně obsazen pro tuto formu psaní, ale je snadné jej počítat:

n = [(a ₁ ; b ₁ ; c ₁ ) * (a ₂ ; b ₂ ; c ₂ )]

Úhel mezi přímkami

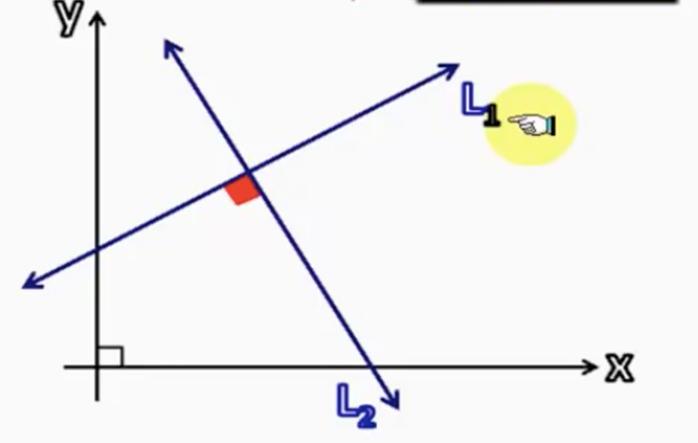
Je-li rovnost vektorů pro každou přímku známa, je úhel mezi nimi snadný. Chcete-li to provést, stačí použít vlastnosti skalárního produktu pro vodicí segmenty přímky. Pokud jsou vodítka vektoru označena symboly v¯ a u¯, pak požadovaná vzorec bude mít podobu:

α = arkkos (| (v¯ *)) | / (| v | | * | | | | |))

Vzhledem k tomu, že v případě průniku přímky jsou vytvořeny dva páry stejných úhlů, pak se zaujme ostrý úhel jako skutečný úhel mezi nimi. Z tohoto důvodu obsahuje vzorec znaménko modulu v čitateli.

Tento vzorec pro dvojrozměrný případ je vždy platný. Výsledná hodnota 0 ^o říká, že přímé linie se neprotínají, ale jsou paralelní.

Pokud jde o prostor v prostoru, kromě výpočtu podle vzorce je nutné provést dodatečné výpočty. Jsou spojeny s nalezením průsečíku dotyčných objektů. Faktem je, že ve vesmíru lze získat konečnou hodnotu úhlu α, ale přímé linie se nebudou protínat, protože se mohou protínají.

Rovina, čára a úhel jejich křižovatky

Chcete-li najít úhel mezi přímkou ​​a rovinou, stačí znát rovnici pro každý z těchto objektů. Úhel mezi nimi je úhel dvou protínajících se čar, z nichž jedna je původní a druhá patří rovině a je projekcí původní čáry na ni. Níže uvedený obrázek ukazuje rovinu, kterou přímka protíná pod úhlem α.

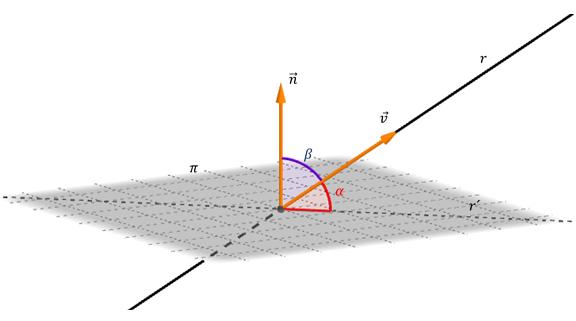
Je-li řídící vektor přímého vektoru označen v ¯ a normál k rovině je n¯ (viz obr.), Pak se vypočítá úhel α pomocí vzorce

α = arcsin (| (v¯ * n¯) | / (| v¯ | * | n¯ |))

Všimněte si, že v tomto vzorci, na rozdíl od podobného výrazu pro dvě protínající přímky, se používá funkce arcsine, nikoliv funkce kosinového oblouku.

Vzdálenost mezi přímkami v rovině a rovinou a přímkou ​​v prostoru

Pro výpočet vzdálenosti mezi předmětnými předměty v geometrii je soubor vzorců. Aplikace výrazu z něj závisí na formě, ve které jsou roviny a čáry uvedeny.

Jsou-li dvě rovné čáry uvedeny v rovině v obecné rovině, vzdálenost mezi nimi může být vypočítána následovně:

d = | A * x ₁ + B * y ₁ + C | / √ (A ² + B ² )

Zde x ₁ a y ₁ jsou souřadnice libovolného bodu na jedné přímce a koeficienty A, B, C jsou odebírány pro druhou přímku. Tento vzorec platí, jsou-li čáry navzájem paralelní. Pokud se protínají, je vzdálenost nula.

Vzdálenost mezi čarou a letadlem je nulová. Je-li přímka rovnoběžná s rovinou, vypočte se odpovídající vzdálenost jako:

d = A * x ₁ + B * y ₁ + C * z ₁ + D | / √ (A ² + B ² + C ² )

Kde souřadnice patří k libovolnému bodu na trati.

Úloha: Určete úhel mezi přímkou ​​a rovinou

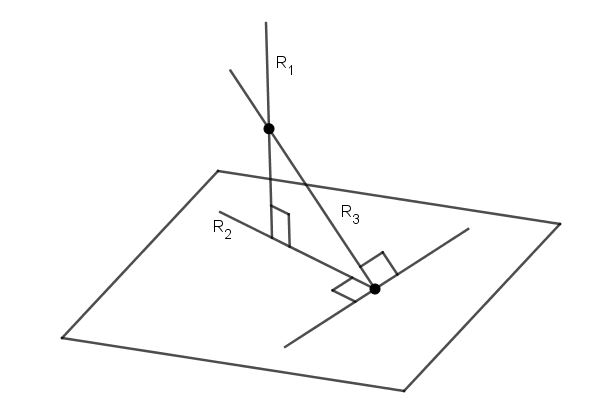
Vzhledem k přímce a rovině:

(x, y; z) = (1; 2; 0) + λ * (- 1; 1; 4);

-5 * x + y - 3 = 0

Jaký je úhel mezi přímkou ​​a rovinou?

Napsali jsme vodítka vektoru v¯ a n¯:

v = (-1; 1; 4);

n¯ = (-5; 1; 0)

Nahraďte je ve vhodném vzorci pro α, dostaneme:

α = arcsin (| 5 + 1 + 0 | / (√18 * √26)) ≈ 16,1 ^o

Úloha: najít vzdálenost mezi přímkami

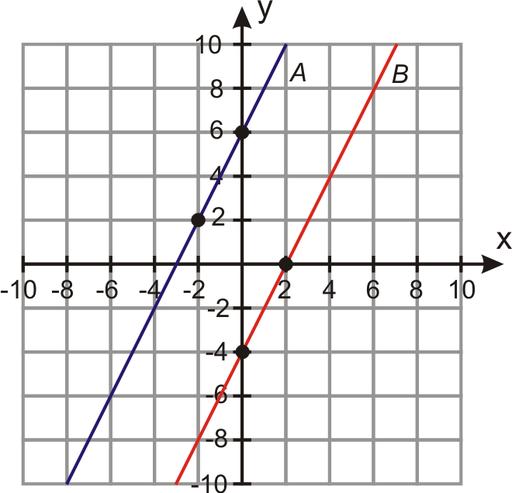
Vzhledem k dvěma rovnicím přímky v dvojrozměrném prostoru:

y = 3 x x 1;

y = 3 * x + 3

Jaká je vzdálenost mezi nimi?

Vzhledem k tomu, že koeficienty k pro oba objekty jsou stejné (rovnající se 3), probíhá paralelní přímky.

Pro výpočet vzdálenosti mezi nimi, vezměte libovolný bod první přímky a přepište druhou rovnici obecně, máme:

souřadnice bodu (0; -1);

3 * x - y + 3 = 0, tj. A = 3, B = -1, C = 3

Nyní lze tyto hodnoty nahradit příslušným vzorem:

d = | 3 * 0 -1 * (- 1) + 3 | / √ (9 +1) = 4 / √10 ≈ 1,265

Odpověď je přijata v jednotkách tohoto souřadného systému.