Jak vypočítat diagonáli hranolu rovného čtyřúhelníku?

Prizma je geometrická volumetrická postava, jejíž vlastnosti a vlastnosti jsou studovány na vysokých školách. Obecně platí, že při jeho studiu jsou zohledněny takové objemy a ploše. V tomto článku otevíráme poněkud jinou otázku: dáváme metodu pro určení délky diagonálů hranolů pomocí příkladu čtverhranného tvaru.

Jaký údaj se nazývá hranol?

V geometrii je dána následující definice hranolu: je to trojrozměrná postava, ohraničená dvěma polygonálně identickými stranami, které jsou navzájem rovnoběžné a řadou paralelogramů. Níže uvedený obrázek ukazuje příklad hranolu, který splňuje tuto definici.

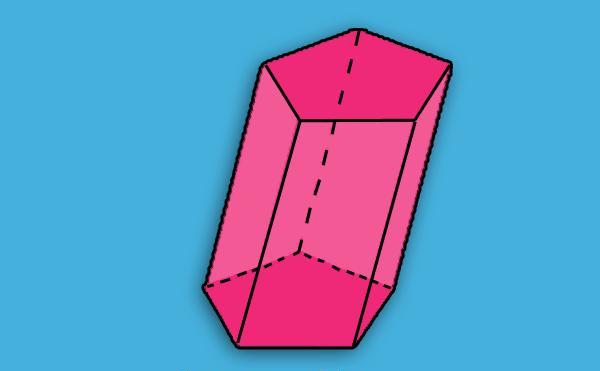
Vidíme, že dva červené pentagony jsou stejné a jsou ve dvou paralelních rovinách. Pět růžových paralelogramů spojuje tyto pentagony s jediným objektem - hranolem. Dva pentagony jsou nazývány základy postavy a její rovnoběžnost jsou boční plochy.

Prismy jsou rovné a šikmé, které se také nazývají obdélníkové a šikmé. Rozdíl mezi nimi je v rozích mezi základnou a bočními plochami. Pro obdélníkový hranol jsou všechny tyto úhly 90 ^o .

Podle počtu stran nebo vrcholů polygonu na základně mluví o hranolovitém, pentagonálním, čtverhranném hranolu a podobně. A pokud je tento polygon správný a samotný hranol je přímka, takový tvar se nazývá správný.

Prismus znázorněný na předcházejícím obrázku je pentagonální. Níže je pentagonový přímý hranol, který je správný.

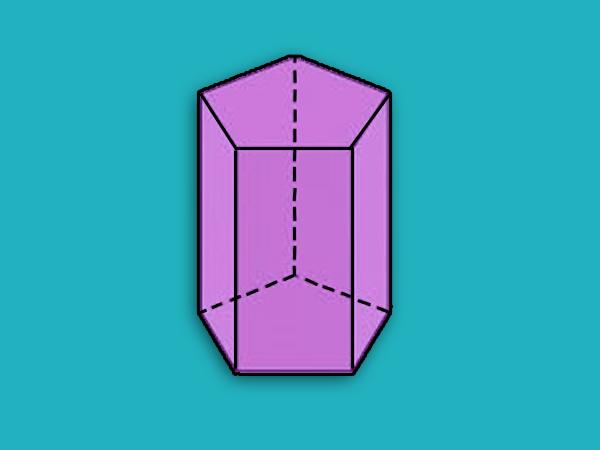
Všechny výpočty, včetně metody určení diagonály hranolu, je vhodné provádět přesně pro správné číslice.

Jaké prvky charakterizují hranol?

Prvky obrázku jsou součásti, které ji tvoří. Konkrétně pro hranol existují tři hlavní typy prvků:

• vrcholy;
• tváře nebo strany;
• žebra.

Tváře jsou základy a bočnice, které v obecném případě představují rovnoběžnost. V hranolu je každá strana vždy jedním ze dvou typů: buďto je to mnohoúhelník nebo rovnoběžník.

Hrany hranolu jsou ty segmenty, které omezují každou stranu obrázku. Stejně jako okraje mají hrany také dva typy: patří k podkladu a bočnímu povrchu nebo patří pouze k boční ploše. První je vždy dvakrát větší než druhá, bez ohledu na typ hranolu.

Vrcholy jsou průsečíky tří okrajů hranolu, z nichž dva leží v rovině základny a třetí leží na dvou bočních plochách. Všechny vrcholy hranolu jsou v rovinách základny postavy.

Čísla popsaných prvků jsou spojena v jedné rovině, která má následující podobu:

P = B + C - 2.

Zde P je počet okrajů, B - vrcholů, C - stran. Tato rovnost se nazývá Eulerova věta pro polyhedron.

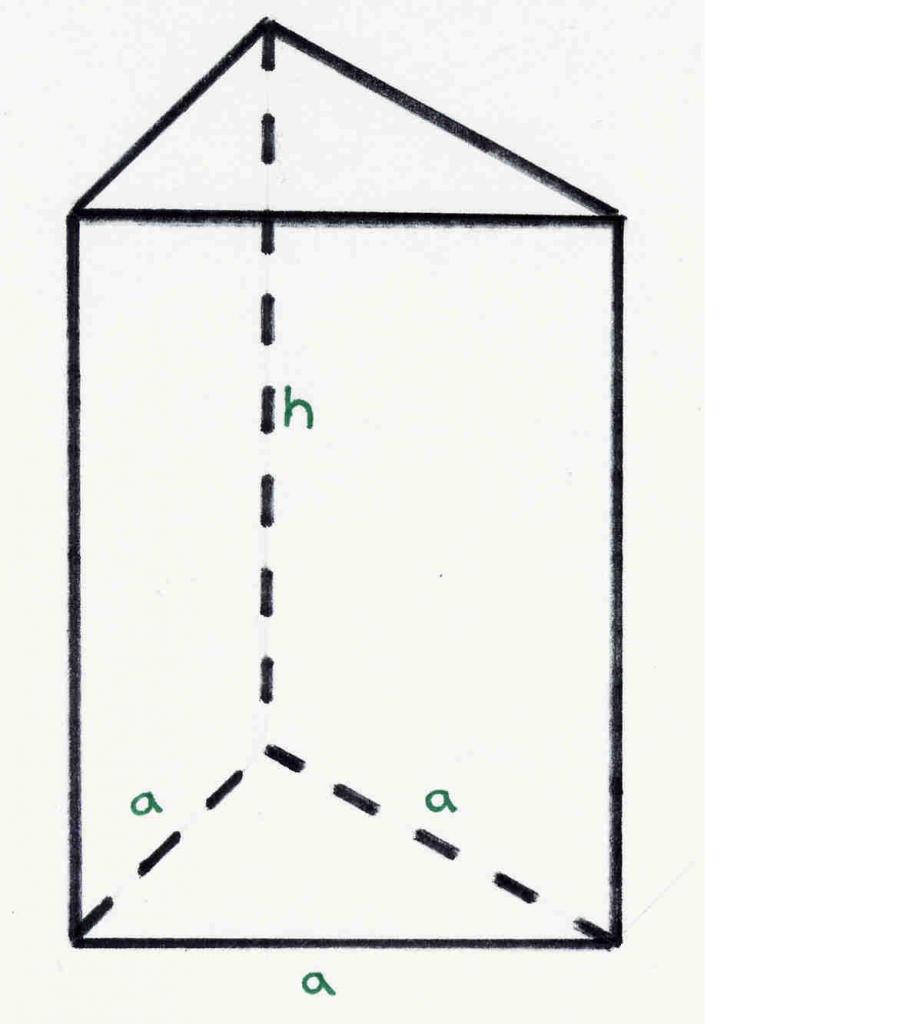
Obrázek ukazuje trojúhelníkový správný hranol. Každý může zjistit, že má 6 vrcholů, 5 stran a 9 okrajů. Tato čísla jsou v souladu s Eulerově teorémi.

Diagonální hranoly

Po vlastnostech, jako je objem a plocha povrchu, v problémech s geometrií se často vyskytují informace o délce dané diagonály uvažovaného čísla, které jsou buď uvedeny, nebo je třeba je nalézt pomocí jiných známých parametrů. Zvažte, jaké jsou diagonály hranolu.

Všechny úhlopříčky lze rozdělit na dva typy:

1. Ležel v rovině tváří. Spojují nesousedící vrcholy buď s polygonem na bázi hranolu nebo rovnoběžníkem bočního povrchu. Hodnota délky takových úhlopříček je určena na základě znalostí délky příslušných okrajů a úhlů mezi nimi. Pro určení diagonálů paralelogramů se vždy používají vlastnosti trojúhelníků.
2. Ležící uvnitř objemu hranolu. Tyto úhlopříčky spojují špičky dvou základen, které nejsou jednolité. Tyto diagonály jsou zcela uvnitř postavy. Jejich délka je poněkud obtížnější k výpočtu než u předchozího typu. Metoda výpočtu zahrnuje zohlednění délky hran a podstavce a rovnoběžnost. U rovných a pravidelných hranolů je výpočet poměrně jednoduchý, protože se provádí pomocí pythagorské věty a vlastností trigonometrických funkcí.

Níže jsou uvedeny příklady výpočtu různých úhlů.

Diagonální strany čtyřhranného přímého hranolu

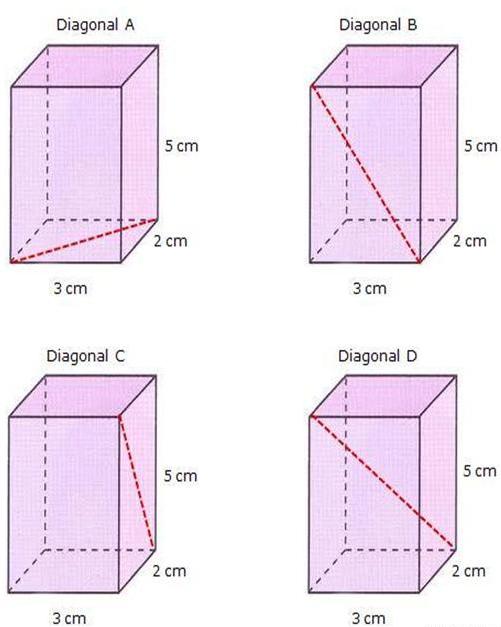
Obrázek výše ukazuje čtyři identické rovné hranoly a jsou uvedeny jejich hrany. Na hranolích s diagonálem A, diagonálem B a úhlopříčkou C je čárkovaná červená čára zobrazena diagonálem tří různých tváří. Vzhledem k tomu, že hranol je rovný o výšce 5 cm a její základna je reprezentována obdélníkem se stranami 3 cm a 2 cm, je snadné najít označené úhlopříčky. Chcete-li to provést, použijte Pythagorovskou větu.

Délka úhlopříčky základny hranolu (diagonál A) se rovná:

D _A = √ (3 ² + ^{2 2} ) = √ 13 ≈ 3 606 cm.

Pro boční stranu hranolu je diagonální (viz diagonální B):

D _B = √ (3 ² + 5 ² ) = √ 34 ≈ 5,831 cm.

Nakonec je délka další boční diagonály stejná (viz diagonální C):

D _C = √ (2 ² + 5 ² ) = √ 29 ≈ 5,385 cm.

Délka vnitřní diagonály

Nyní vypočítáme délku úhlopříčky čtyřúhelníku, která je znázorněna na předcházejícím obrázku (Diagonal D). To není tak obtížné udělat, pokud zjistíte, že jde o hypotenzu trojúhelníku, ve kterém bude výška hranolu (5 cm) a úhlopříčka D _A zobrazená na obrázku vlevo nahoře (Diagonal A) nohy. Pak dostaneme:

D _D = √ (D _A ² + 5 ² ) = √ (2 ² +3 ² + 5 ² ) = √38 ≈ 6,164 cm.

Správný hranol čtyřhranný

Úhlopříčka pravidelného hranolu, jehož základ je čtverec, se počítá stejným způsobem jako ve výše uvedeném příkladu. Odpovídající vzorec je:

D = √ (2 * a ² + c ² ).

Kde a a c jsou délky boční strany a boční hrany.

Všimněte si, že ve výpočtech jsme použili pouze Pythagorovu větu. Pro určení délky úhlopříček pravidelných hranolů s velkým počtem vrcholů (pentagonální, šestihranná atd.) Je již potřeba použít trigonometrické funkce.