Jak vypočítat objem míče a jiné nuance ve výpočtech

Než začnete studovat koncept míče, jaký je objem míče, zvážit vzorce pro výpočet jejích parametrů, musíte si připomenout koncept kruhu, který byl dříve studován v průběhu geometrie. Koneckonců, většina akcí v trojrozměrný prostor jsou podobné nebo pocházejí z dvojrozměrné geometrie, korigované pro vzhled třetího souřadného bodu a třetího stupně.

Co je to kruh?

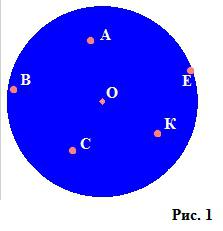
Kruh je číslo na kartézské rovině (znázorněné na obrázku 1); Nejčastěji tato definice zní jako "místo všech bodů v rovině, vzdálenost, od které k určitému bodu (středu) nepřesahuje určité ne záporné číslo nazvané poloměr."

Jak je vidět z obrázku, bodem O je střed obrazu a množina absolutně všech bodů, které vyplňují kruh, například A, B, C, K, E, nejsou delší než zadaný poloměr (nepřesahují kružnici zobrazenou na obrázku 2).

Pokud je poloměr nulový, pak se kruh změní na bod.

Problémy s porozuměním

Žáci často zaměňují tyto pojmy. Snadno si to pamatujete tím, že vytvoříte analogii. Obruč, který děti otáčejí ve třídách tělesné výchovy, je kruh. Pochopení této skutečnosti nebo zapamatování, že první písmena obou slov jsou "O", děti mnemologicky pochopí rozdíl.

Zavedení konceptu "míče"

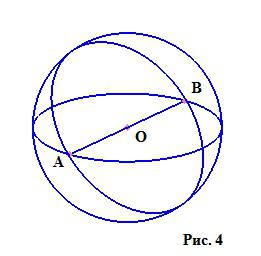
Koule je těleso (obr. 3), ohraničené sférickým povrchem. Jaký je "sférický povrch" ze své definice: toto je geometrická poloha všech bodů na povrchu, jejichž vzdálenost od daného bodu (středu) nepřesahuje určité ne záporné číslo, nazývané poloměr. Jak vidíme, koncepty kruhu a sférického povrchu jsou podobné, liší se pouze prostory, ve kterých se nacházejí. Pokud nakreslíme míč ve dvourozměrném prostoru, získáme kruh, jehož hranice je kružnice (u koule je hranice sférická plocha). Na obrázku vidíme sférický povrch s poloměrem OA = OB.

Míč je zavřený a otevřený

Ve vektorových a metrických prostorách jsou také zvažována dvě koncepce týkající se sférického povrchu. Jestliže míč obsahuje tuto kouli sama o sobě, pak se nazývá uzavřená, a pokud ne, pak je míč otevřený. Jedná se o více "pokročilé" pojmy, jsou studovány v ústavu s úvodem k analýze. Pro jednoduché, dokonce i pro domácnosti se postačí, že budou dodrženy vzorce, které jsou studovány v průběhu stereometrie 10-11 tříd. Jsou to takové pojmy, které jsou přístupné téměř každému průměrnému vzdělanému člověku, který bude dále diskutován.

Koncepty, které potřebujete znát pro následující výpočty

- poloměr a průměr.

- Poloměr koule a jeho průměr je určen stejným způsobem jako kruh.

- Radius - segment spojující libovolný bod na hranici míče a bod, který je středem míče.

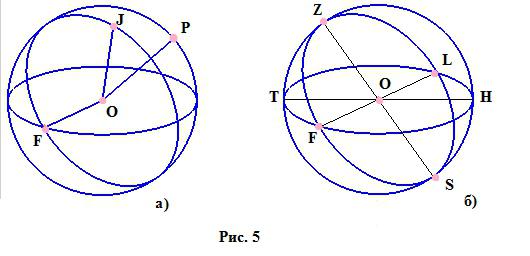
- Průměr - segment, který spojuje dva body na hranici míče a prochází jeho středem. Obrázek 5a jasně ukazuje, které segmenty jsou poloměry koule a obrázek 5b ukazuje průměry koule (segmenty procházející bodem O).

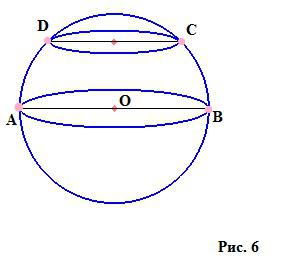
Sekce koule (koule)

Každá část koule je kruh. Pokud prochází středem míče, nazývá se to velkým kruhem (kruh s průměrem AB), zbývajícími částmi jsou malé kruhy (kruh s průměrem DC).

Oblast těchto kruhů se vypočte podle následujících vzorců:

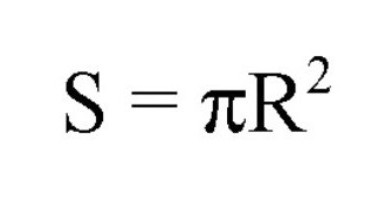
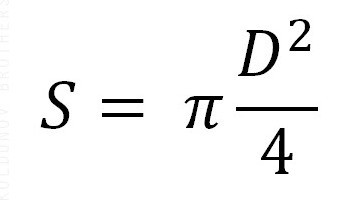
Zde S je označení oblasti, R je poloměr, D je průměr. Také je přítomna konstanta 3,14. Ale nezaměňujte to pro výpočet plochy velkého kruhu za použití poloměru nebo průměru koule (koule) a pro určení oblasti jsou rozměry poloměru vyžadovány jen pro malý kruh.

Existuje bezpočet takových úseků, které procházejí dvěma body stejného průměru ležícími na hranici míče. Jako příklad - naše planeta: dva body na severním a jižním pólu, které jsou konce zemské osy a v geometrickém smyslu - konce průměru a meridiány, které procházejí těmito dvěma body (obr. 7). To znamená, že počet velkých kruhů ve sféře má nekonečno v počtu.

Kulové části

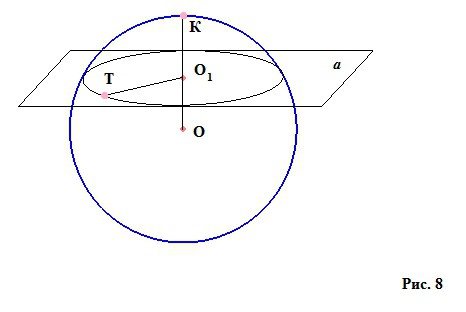
Pokud odříznete kouli z koule pomocí jisté roviny (obr. 8), pak se bude nazývat kulový nebo sférický segment. Bude mít výšku - kolmou od středu řezné roviny k sférickému povrchu O ₁ K. Bod K na sférickém povrchu, ke kterému se dostává výška, se nazývá vrchol sférického segmentu. A malý kruh s poloměrem O ₁ T (v tomto případě, podle obrázku, letadlo neprošlo středem koule, avšak pokud průřez prochází středem, potom bude kruhový úsek velký), vytvořený v okamžiku, kdy bude segment koule odříznut, bude nazýván základem našeho kusu koule - sférický segment.

Pokud spojujete každý bod základny sférického segmentu se středem koule, získáváme tvar nazývaný "sektor koulí".

Pokud dvě roviny, které jsou navzájem rovnoběžné, procházejí koulí, pak ta část koule, která je mezi nimi uzavřena, se nazývá sférická vrstva (obrázek 9, který ukazuje kouli s dvěma rovinami a sférickou vrstvou zvlášť).

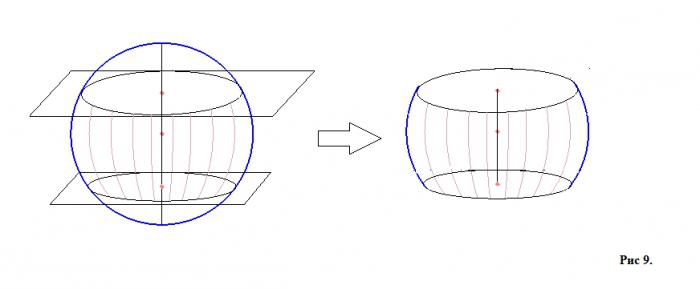
Povrch (zvýrazněná část na obrázku 9 vpravo) této části koule se nazývá pás (opět pro lepší pochopení lze analogicky vyvodit analogii s globem, a to s jeho klimatickými zónami - arktickými, tropickými, střednědobými atd.) A kruhové úseky budou základy míčová vrstva. Výška vrstvy je částí průměru vytaženého kolmo k řezným rovinám z center základen. Existuje také koncept koule. Vzniká v případě, kdy roviny, které jsou vzájemně rovnoběžné, neprotínají kouli, ale dotýkají se jí v jednom bodě.

Vzorec pro výpočet objemu kuličky a jejího povrchu

Koule je tvořena otočením kolem pevného průměru polkruhu nebo kruhu. Pro výpočet různých parametrů tohoto objektu nepotřebujete příliš mnoho dat.

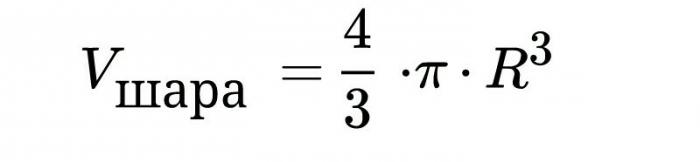
Objem míče, vzorec pro výpočet, který je uveden výše, je odvozen pomocí integrace. Rozumíme bodům.

Považujeme kruh ve dvourozměrné rovině, protože jak je uvedeno výše, je to kruh, který tvoří základ konstrukce míče. Používáme pouze čtvrtou část (obrázek 10).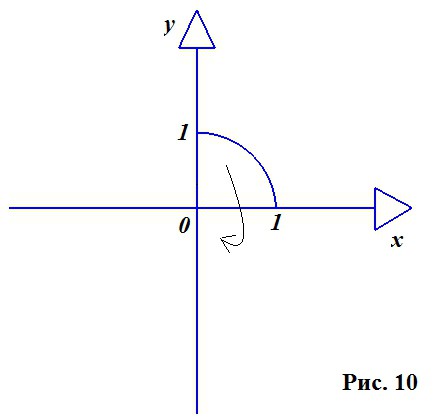

Vezměte kruh s poloměrem jednotky a centrem původu. Rovnice takového kruhu je následující: X ² + Y ² = R ² . Vyjadřujeme zde Y: Y ² = R ² - X ² .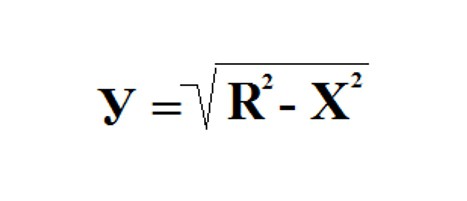

Ujistěte se, že výsledná funkce je ne-záporná, spojitá a klesající na segmentu X (0; R), protože hodnota X v případě, kdy považujeme čtvrtinu kružnice, leží od nuly až po hodnotu poloměru, tedy na jednu.

Další věc, kterou děláme, je otočení naší čtvrté kružnice kolem osy x. Výsledkem je hemisféra. Abychom zjistili jeho objem, uchýlíme se k metodám integrace.

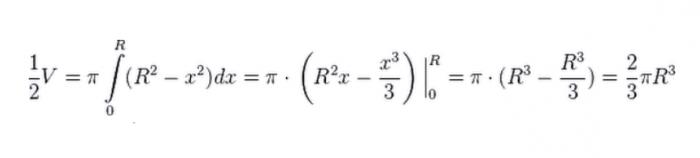
Vzhledem k tomu, že tento objem je pouze hemisférou, zdvojnásobíme výsledek, odkud se zjistí, že objem míče se rovná:

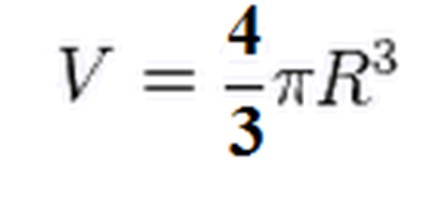
Malé nuance

Pokud je nutné vypočítat objem kuličky přes jeho průměr, nezapomeňte, že poloměr je poloviční průměr a tuto hodnotu nahraďte ve výše uvedeném vzorci.

Také vzorec pro objem míče lze dosáhnout přes plochu jeho hraniční plochy - koule. Připomeňme si, že oblast koule je vypočtena podle vzorce S = 4πr ² , integrující to, že také dosáheme výše uvedeného vzorce pro objem míče. Ze stejných vzorců lze vyjádřit poloměr, pokud stav problému obsahuje hodnotu objemu.