Jak provést úplnou funkční studii

V tomto článku se podíváme na schéma studia funkce a také uvádíme příklady studií o extrémech, monotonicitě a asymptotech této funkce.

Schéma

1. Oblast funkce existence (DHS).
2. Průsečík funkce (pokud existuje) s osami souřadnic, znaménkem funkce, paritou, periodicitou.
3. Body zlomu (jejich rod). Kontinuita. Vertikální asymptoty.
4. Monotónní a extrémní body.
5. Inflexní body Bubeník
6. Studium funkce v nekonečnu, na asymptotech: horizontální a šikmé.
7. Plotování.

Monotónní studie

Věta. Je-li funkce g spojitá na [a, b] , diferencovaná (a, b) a g '(x) ≥ 0 (g' (x) ≤0) , xє [a, b] .

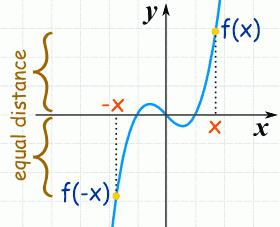
Příklad:

y = 1: 3x ³ - 6: 2x ² + 5x.

DHS: xR

y '= x ² + 6x + 5.

Najít intervaly konstantních znaků y ' . Jelikož y ' je základní funkce, může znaménko změnit pouze v bodech, kde se změní na nulu nebo neexistuje. Její DHS: xR .

Najít body, jejichž derivát je 0 (nula):

y '= 0;

x = -1; -5.

Takže y roste na (-∞; -5) a na [-1; + ∞), y sestupně do [1; 2] .

Extrémní studie

T. x _{0 se} nazývá maximální bod (max) na množině A funkce g, když je v tomto okamžiku považována hodnota g (x ₀ ) ≥ g (x), xєA .

T. x _{0 se} nazývá minimální bod (min) funkce g na množině A, když je v tomto okamžiku bráno nejmenší g (x ₀ ) ≤ g (x), xєA.

Na množině A jsou maximální body (max) a minimum (min) nazývány extrémními body g . Takové extrémy se také nazývají absolutní extrémy na sadě .

Pokud x ₀ je extrémní bod g v nějakém okrese, pak x ₀ se nazývá bod lokálního nebo lokálního extrému (max nebo min) g.

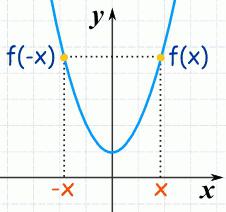
Věta (požadovaná podmínka). Je-li x ₀ extrémním bodem (lokální) funkce g , potom derivát neexistuje nebo je v tomto r. 0 (nula) rovný.

Definice Kritické body jsou body s neexistujícím nebo rovným 0 (nula) derivátu. Tyto datové body jsou pro extremum podezřelé.

Věta (podmínka č. 1). Je-li funkce g kontinuální v určitém sousedství t. X ₀ a znaménko změní jeho derivaci při přechodu, potom daný bod je extrémem g .

Věta (podmínka č. 2). Nechť funkce v určitém okrsku je dvakrát diferencovaná a g '= 0, g' '> 0 (g' '<0) , pak tento bod je bod maximální (max) nebo minimální (min) funkce.

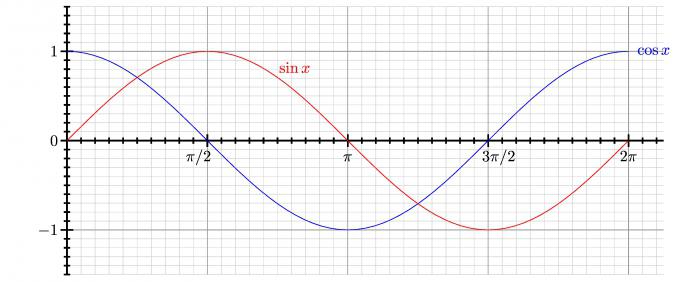
Studium výbuchu

Funkce se nazývá konvexní (nebo konkávní) v intervalu (a, b), pokud graf funkce není vyšší než sekundu v intervalu pro libovolný x s (a, b), který prochází těmito body .

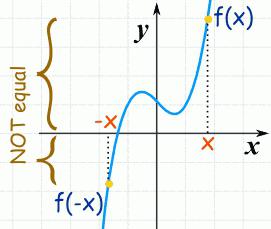
Funkce bude konvexně striktně dolů na (a, b) , pokud - graf leží pod průsečíkem mezery.

Funkce se nazývá konvexní (konvexní) v intervalu (a, b) , jestliže pro všechny body t s (a, b) graf funkce na daném intervalu není nižší než průsečík procházející úsečky v těchto bodech .

Funkce bude přísně konvexní směrem nahoru (a, b ), pokud - graf na intervalu leží nad sekantem.

Je-li funkce v okrese bodem je kontinuální a po t. x ₀ funkce změní konvexnost při přechodu, tento bod se nazývá inflexní bod funkce.

Asymptote test

Definice Přímá linka se nazývá asymptote g (x), jestliže v nekonečné vzdálenosti od původu souřadnic přistupuje bod funkčního grafu: d (M, l).

Asymptoty mohou být svislé, vodorovné a šikmé.

Vertikální čára s rovnicí x = x ₀ bude asymptote vertikálního grafu funkce g pokud v t. x _{0 je} nekonečná mezera, tj. alespoň jedna levá nebo pravá hranice v tomto bodě je nekonečna.

Studium funkce na segmentu na hodnotě nejmenší a největší

Pokud je funkce spojitá na [a, b] , pak podle Weierstrassovy věty existuje největší hodnota a nejmenší hodnota na tomto segmentu, tj. Existují body t, které patří k [a, b] tak, že g (x ₁ ) <g (x ₂ ), x ₂ [a, b]. Z věty o monotonii a extrémích získáváme následující schéma pro studium funkce na segmentu pro nejmenší a největší hodnotu.

Plán

1. Najděte derivát g '(x) .
2. Najděte hodnotu funkce g v těchto bodech a na koncích segmentu.
3. Získané hodnoty porovnávají a vybírají nejmenší a největší.

Poznámka Chcete-li studovat funkci v konečném intervalu (a, b) , nebo na nekonečné (-∞; b); (-∞, + ∞) na hodnotě max a min, pak v plánu namísto hodnot funkce na koncích mezery se hledají příslušné jednostranné hranice: namísto f (a), f (a +) = limf (x) (-b) Funkce LDU můžete najít v intervalu, protože absolutní extrémy nemusí v tomto případě nutně existovat.

Aplikace derivátu na řešení aplikovaných problémů na extremum určitých veličin

1. Vyjádřete tuto hodnotu z hlediska ostatních hodnot z stavu problému tak, že je funkcí pouze jedné proměnné (je-li to možné).
2. Určete dobu změny této proměnné.
3. Proveďte studium funkce na intervalu při hodnotách max a min.

Úkol. Je třeba postavit obdélníkovou plošinu pomocí mřížkových mřížek proti stěně tak, aby na jedné straně zasahovala do zdi a na ostatních třech je oplocena mřížkou. Při jakém poměru stran bude největší plocha takovéhoto místa?

S = xy je funkce dvou proměnných.

S = x (a - 2x) - funkce první proměnné ; x є [0; a: 2].

S = ax - 2x ² ; S '= a - 4x = 0, x "R, x = a: 4.

S (a: 4) = a ² : 8 je nejvyšší hodnota;

S (0) = 0.

Najít druhou stranu obdélníku: = a: 2.

Poměr stran: y: x = 2.

Odpověď zní. Největší plocha se rovná 2/8 , pokud je strana rovnoběžná se stěnou 2krát větší než druhá strana.

Výzkumná funkce. Příklady

Příklad 1

Existuje y = x ³ : (1-x) ² . Provádějte výzkum.

1. DHS: xє (-∞; 1) U (1; ∞).
2. Obecná forma funkce (ani sudá ani lichá) není symetrická kolem bodu 0 (nula).
3. Znaky funkce. Funkce je elementární, takže může měnit znaménko pouze v bodech, kde je 0 (nula) nebo neexistuje.
4. Funkce je elementární, tedy kontinuální na DHS: (-∞; 1) U (1; ∞).

Rozdíl: x = 1;

limx ³ : (1 - x) ² = ∞ - diskontinuita druhého druhu (nekonečná), takže je v bodě 1 vertikální asymptota;

x = 1 je vertikální asymptote rovnice.

5. y '= x ² (3 - x): (1 - x) ³ ;

DHS (y '): x ≠ 1;

x = 1 - kritický bod.

y '= 0;

0; 3 - kritické body.

6. y "= 6x: (l-x) ⁴ ;

Kritická t .: 1, 0;

x = 0 - m. kink, y (0) = 0.

7. Limbe ³ : (1 - 2x + x ² ) = ∞ - neexistuje horizontální asymptota, ale může být nakloněná.

k = 1 je číslo;

b = 2 je číslo.

Proto je asymptote nakloněná y = x + 2 při + ∞ a při - ∞.

Příklad 2

Vzhledem k tomu, že y = (x ² + 1): (x - 1). Provádět a zkoumat. Vytvoření grafu.

1. Doménou existence je celá číselná čára, s výjimkou m. X = 1 .

2. y protíná OY (pokud je to možné) v m (0; g (0)) . Najít y (0) = -1 - t. křižovatka OY .

Najdeme průsečíky grafu s OX řešením rovnice y = 0 . Kořenová rovnice není platná, proto tato funkce neprotíná OX .

3. Funkce je neperiodická. Zvažte výraz

g (-x) ≠ g (x) a g (-x) -g (x) . To znamená, že toto je obecná funkce (ani sudá ani lichá).

4. T. x = 1 mezera má druhý typ. Ve všech ostatních bodech je funkce kontinuální.

5 Studium funkce na extremum:

(x ² - 2x - 1): (x - 1) ² = y '

a vyřešit rovnici y '= 0.

Takže 1 - √2, 1 + √2, 1 - kritické body nebo body možného extrému. Tyto body rozdělují číselnou čáru na čtyři intervaly .

V každém intervalu má derivát určité znaménko, které lze nastavit metodou intervalů nebo výpočtem hodnot derivátu v jednotlivých bodech. V intervalech (-∞; 1 - √2 ) U ( 1 + √2 ; ∞) pozitivní derivace znamená, že funkce roste; pokud xє ( 1 - √2 ; 1) U (1, 1 + √2 ) , pak se funkce snižuje, protože v těchto intervalech je derivát záporný. Prostřednictvím t. X ₁ při přechodu (zleva doprava) změníme odvozený znak z "+" na "-", proto v tomto okamžiku existuje lokální maximum, najdeme

y _max = 2 - 2 √2 .

Když prochází x _2, změní odvozený znak z "-" na "+", proto v tomto okamžiku existuje místní minimum a

y _mix = 2 + 2√2.

T. x = 1 není tak extrémní.

6. 4: (x - 1) ³ = y ".

Na (-∞; 1 ) 0> y " , v tomto intervalu je křivka konvexní; pokud xє ( 1 ; ∞) - křivka je konkávní. V bodě 1 funkce není definována, proto tento bod není bodem inflexe.

7 Z výsledků odstavce 4 vyplývá, že x = 1 je asymptote vertikální křivka.

Horizontální asymptoty chybí.

x + 1 = y je asymptota nakloněná touto křivkou. Neexistují žádné další asymptoty.

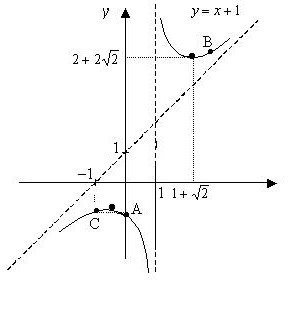
8. Vzhledem k provedenému výzkumu sestavujeme graf (viz výše uvedený obrázek).