Jak najít gcd dvou čísel? "Turbo Pascal" a trochu matematiky

Noví programátoři se často seznamují s prostorem Turbo Pascal prostými úkoly. První úkoly, které uživatel implementuje v kódu: zobrazit jakýkoli text, najít GCD a NOC přirozených čísel vypočítat, kolik čtveřice jsou za měsíc atd. Často existují úkoly s matematickou předpojatostí. Než implementujete své znalosti v programovém kódu, potřebujete studovat další materiály. Například, jak najít GCD a NOC dvou čísel v Turbo Pascal.

Hledání gcd v matematice

Největším společným faktorem je číslo, které je považováno za maximum, když se rozkládá na součásti. Krátká podoba definice jako GCD je zaznamenána. Zvažte například výkres. Zde jsou uvedeny čísla 140 a 175. Největší dělitel je 35, tedy GCD (140.175) = 35.

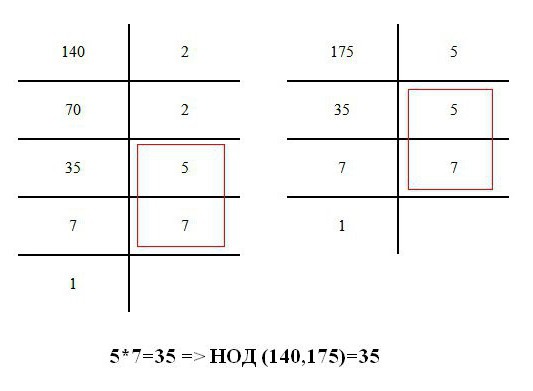
Abyste se vyhnuli dalším otázkám, jak najít GCD dvou čísel, měli byste dodržovat tento algoritmus:

• Najděte nejjednodušší děliče prvního čísla.
• Stejná operace se provádí s druhým číslem.
• Chcete-li najít společné ukazatele v sadě dělitel prvního a druhého čísla.
• Kroužte je perem jiné barvy.
• Vynásobte společné děliče (pokud existuje několik) nebo napište jediný (pokud čísla jsou primární jejich gcd bude rovno 1).

Zvažte následující obrázek. Ukazuje, že ani takové velké číslice jako 816 a 455 nemají GCD, s výjimkou 1.

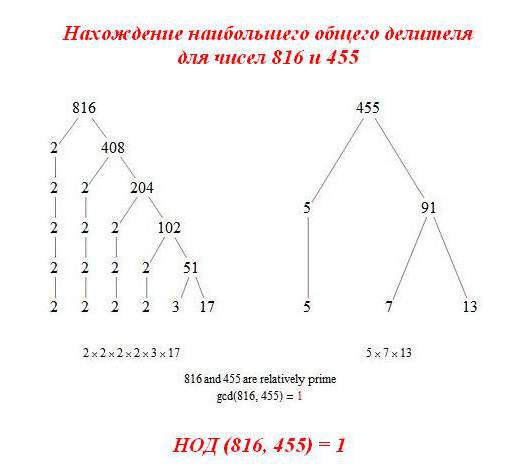
Existuje druhá cesta k nalezení úkolu. Euklidovský algoritmus v matematice je následující:

• Vzhledem k číslům.
• Vybrat by měl být maximální.
• Je rozdělen na minimum.
• Druhé zadané číslo se nyní musí vydělit výsledným zůstatkem.
• První rovnováha je dělena druhou, která je výsledkem předchozí operace.
• Druhá zbytková část je dělena třetím, atd.
• Operace dělení se provádí, dokud zbytek není rovno 0.
• Poslední dělič a splňuje kritérium NOD.

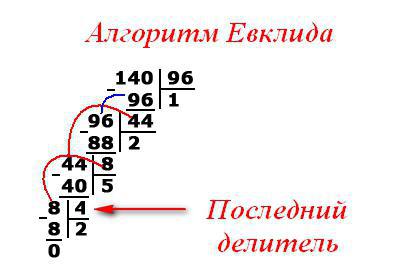
K nalezení GCD více než tří přirozených čísel se doporučuje sledovat schéma práce (uveďte čísla 140, 96, 64):

• V prvním kroku opakujte výše uvedený algoritmus pro první dvě čísla.
• Najděte GCD nalezeného dělitele a zadané třetí číslo.
• Najděte GCD výsledného dělitele a čtvrtého čísla atd.

Hledání NOC v matematice

Jestliže programování vyvolá otázku, jak najít GCD dvou čísel, pak je nutně spojeno s druhým číslem: zjištění NOC. Nejmenší společný násobek dvou čísel je takové minimální přirozené číslo, které může být sdíleno prvním a druhým.

První způsob:

• Dané dvě nebo více čísel.
• Napište všechny násobky pro každou pozici.
• Vyberte nejmenší společný násobek.

Druhý způsob:

• Rozdělte všechna čísla na primární faktory.
• Napište do řádku všechny děliče prvního čísla a přidejte zde ty faktory, které jsou v jiných rozšířeních, ale chybí v první.
• Vypočítejte produkt.

GCD v Pascalu: algoritmus práce

Jak najít gcd dvou čísel? "Pascal" je programovací jazyk, ve kterém bude napsán kód. Nejprve je třeba dodržet algoritmus uvedený výše. A tady matematika přijde k záchraně. Algoritmus úkolu pomůže najít GCD dvou přirozených čísel. V Turbo Pascalu to vypadá takto:

• Zobrazte výzvu, abyste z klávesnice zadali dvě ne záporná čísla.
• Spusťte cyklus while, kde podmínkou je číslo 1 <> číslo 2 (podmíněně, a a b).
• Těleso cyklu zahrnuje následující akce: pokud a> b, pak a: = a - b, jinak b: = b - a.
• Zobrazte výsledek.

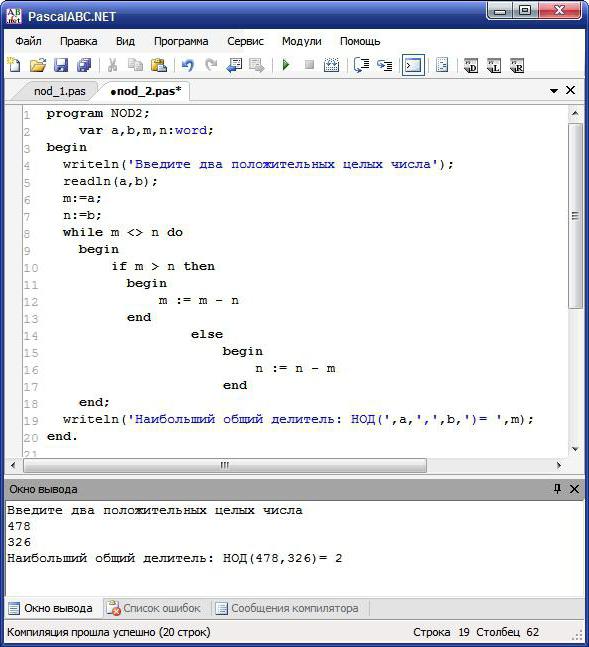
NOD v Pascalu: Euclidean řešení

Jak najít GCD dvou čísel jednoduchou, ale účinnou metodou?

• Zadání pozitivních čísel.
• Volání do písemné funkce, která vypočítá gcd. Samotná funkce provádí následující akce: kontrola stavu, které číslo je větší; přiřazení počátečních dat jiným proměnným; v cyklu s předpokladem (r2 <> 0, tj. dokud proměnná není rovna 0), je nalezen zbytek dělení a výsledky jsou přiřazeny proměnným; přiřazení názvu funkce konečného výsledku.
• Zobrazte výsledek na obrazovce.

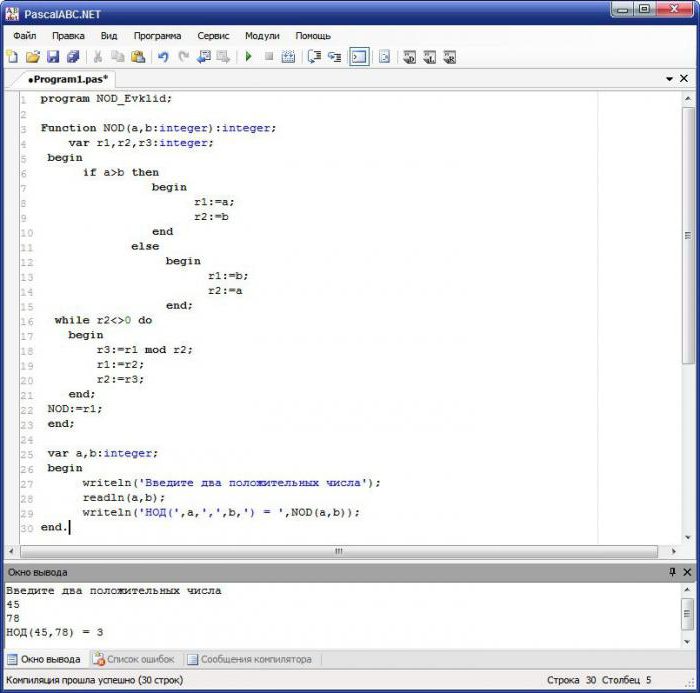
Mnoho programátorů se domnívá, že oba možnosti hledání GCD jsou velmi podobné, takže na internetu může být první metoda vydána jako euklidovský algoritmus.

NOC v programu Pascal: Jak je program uspořádán?

Byly již zváženy dva algoritmy, které vysvětlují, jak najít GCD dvou čísel. Nyní se dozvíte, jak vyhledávací program NOC vypadá v programu Turbo Pascal. Algoritmus práce při programování je následující:

• Zadejte dvě čísla.
• Přiřazení dvou dalších proměnných k daným hodnotám.
• Hledání produktu původních prvků.
• Ve smyčce s předpokladem (zatímco) nastavte podmínku: jestliže první číslo je větší než druhé (n> m), pak výsledek (n: = n - m) najděte odečtením; jinak proveďte tuto operaci, ale v opačném směru (m: = m - n).
• Zobrazte výsledek, ve kterém nalezený produkt bude dělen rozdělením funkce div číslem m.

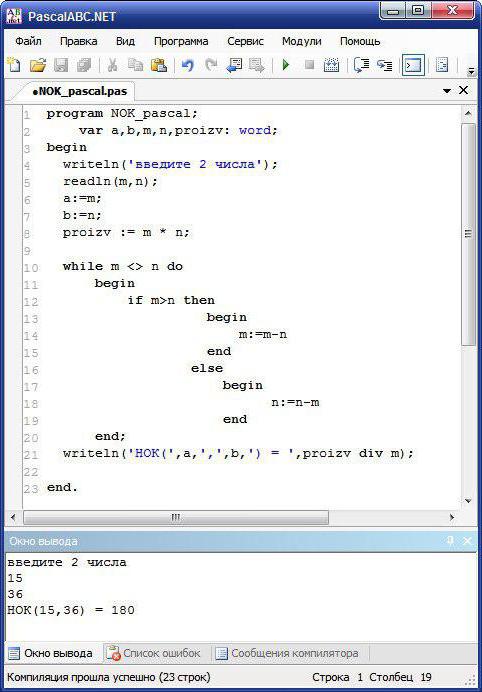
Jaké jsou proměnné a a b zavedeny? Pro správné zobrazení výsledku. V cyklu s předpokladem jsou původní hodnoty proměnných ztraceny, takže není možné výstupní hodnoty m, n zadané uživatelem v závorkách. Samozřejmě, řádek 21 může být značně zjednodušen psaním pouze writeln (proizv div m). Ale uživatel, který bude poprvé seznámen s programem, nechápe, co se na obrazovce zobrazuje.

Ruční sledování:

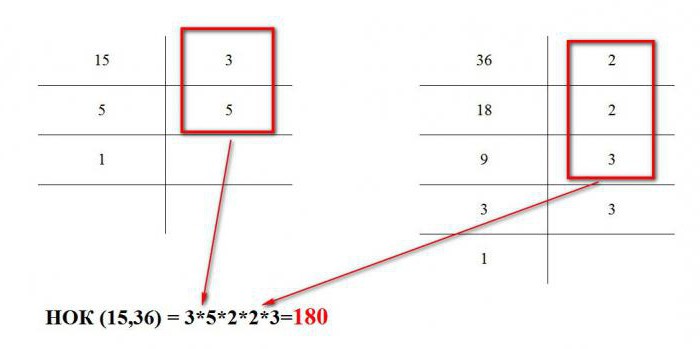
Jak můžete vidět, není nic těžkého najít řešení GCD a NOC: ani v Pascalu, ani ve skutečnosti v matematice.