Pohyb nabité částice v magnetickém poli: vzorce. Pohyb nabitých částic v jednotném magnetickém poli

Jak je známo, elektrické pole je obvykle charakterizováno velikostí síly, se kterou působí na zkušební jednotce elektrický náboj Magnetické pole je tradičně charakterizováno silou, kterou působí na vodič s "jediným" proudem. Nicméně, jak to proudí, v magnetickém poli dochází k uspořádanému pohybu nabitých částic. Proto můžeme určit magnetické pole B v určitém bodě prostoru z pohledu magnetické síly F _B , kterou pole působí na částicu, když se v ní pohybuje rychlostí v.

Obecné vlastnosti magnetické síly

Pokusy, při kterých byl pozorován pohyb nabitých částic v magnetickém poli, poskytují následující výsledky:

• Velikost magnetu FB magnetické síly působící na částic je úměrná náboji q a rychlosti v částic.
• Pokud pohyb nabité částice v magnetickém poli probíhá paralelně k vektoru tohoto pole, pak síla působící na něj je nula.
• Když vektor rychlosti částic vytvoří nějaký úhel θ 0 s magnetickým polem, působí síla ve směru kolmém na v a B; tj. F _{B je} kolmá na rovinu vytvořenou v a B (viz obrázek níže).
• Velikost a směr F _B závisí na rychlosti částic a na velikosti a směru magnetického pole B.
• Směr síly působící na kladný náboj je protilehlý ke směru stejné síly působící na záporný náboj pohybující se ve stejném směru.
• Velikost magnetické síly působící na pohybující se částice je úměrná sinu θ úhlu θ mezi vektory v a B.

Lorenzova síla

Tyto pozorování můžeme shrnout zaznamenáním magnetické síly jako F _B = qv x B.

Když se nabitá částicka pohybuje v magnetickém poli, Lorentzova síla F _B s pozitivním q je směrována podél vektorového produktu vx B. Je to definice kolmá jak na v, tak na B. Takovou rovnici považujeme za pracovní definici magnetického pole v určitém bodě prostoru. To znamená, že je definován ve smyslu síly působící na částici, jak se pohybuje. Takže pohyb nabité částice v magnetickém poli může být krátce definován jako pohyb pod působením této síly.

Nabíjení pohybující se rychlostí v za přítomnosti elektrického pole E a magnetického B je ovlivněno jak elektrickou silou qE, tak magnetickou qv x B. Celkový efekt, který na ni působí, je F _L = qE + qv x B. To se nazývá tak: plná moc Lorentze.

Pohyb nabitých částic v jednotném magnetickém poli

Nyní zvažujeme speciální případ kladně nabitých částic, pohybujících se v jednotném poli, s počátečním veličinou rychlosti kolmým k němu. Předpokládejme, že vektor pole B je směrován na stránku. Níže uvedený obrázek ukazuje, že se částice pohybuje v kruhu v rovině kolmé na B.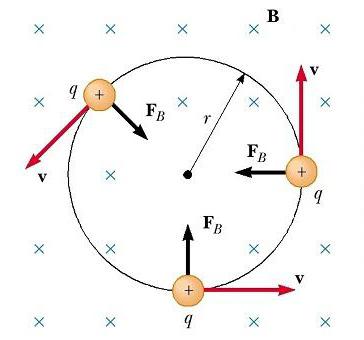

Kruhový pohyb nabité částice v magnetickém poli nastává, protože magnetická síla F _{B je} orientována v pravém úhlu k v a B a má konstantní hodnotu qvB. Jak síla odkládá částice, směry v a F _{B se} mění plynule, jak je znázorněno na obrázku. Vzhledem k tomu, že F _{B je} vždy směrován směrem ke středu kruhu, mění pouze směr v, nikoli jeho hodnotu. Jak je znázorněno na obrázku, pohyb kladně nabitých částic v magnetickém poli probíhá proti směru hodinových ručiček. Je-li q záporné, otáčení bude probíhat ve směru hodinových ručiček.

Dynamika kruhového pohybu částice

Jaké parametry charakterizují výše popsaný pohyb nabité částice v magnetickém poli? Vzorce pro jejich určení můžeme získat, pokud budeme vycházet z předchozí rovnice a rovnat se F _B odstředivá síla potřebná k udržení kruhové trajektorie pohybu: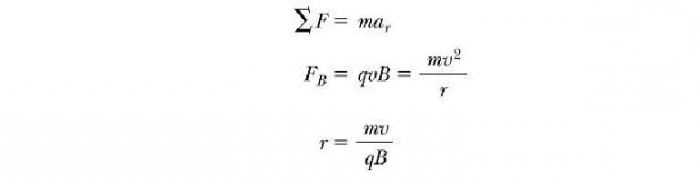

To znamená, že poloměr kruhu je úměrný hybnosti mv částice a nepřímo úměrný velikosti náboje a magnetického pole. Úhlová rychlost částic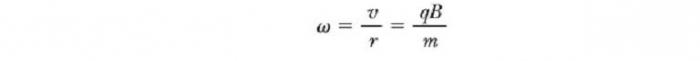

Doba, po kterou se nabitá částice pohybuje v magnetickém poli v kruhu, se rovná obvod dělená jeho lineární rychlostí: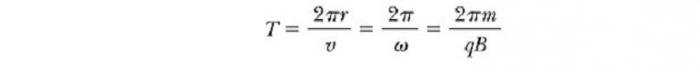

Tyto výsledky ukazují, že úhlová rychlost částice a doba kruhového pohybu nezávisí na lineární rychlosti nebo na poloměru oběžné dráhy. Úhlová rychlost ω je často nazývána cyklotron. frekvence (kruhové), protože nabité částice s ním cirkulují v typu akcelerátoru nazývaném cyklotron.

Pohyb částice pod úhlem vůči vektoru magnetického pole

Pokud vektor vektoru rychlosti částic v vytváří libovolný úhel vzhledem k vektoru B, pak jeho dráha je šroubovice. Například pokud je rovnoměrné pole směrováno podél osy x, jak je znázorněno na následujícím obrázku, v tomto směru neexistuje žádná součást magnetické síly FB. Výsledkem je, že akcelerační složka je _x = 0 a x-složka rychlosti částic je konstantní. Nicméně magnetická síla F _B = qv x B způsobuje časovou změnu komponent rychlosti v _y a v _z . Výsledkem je, že nabitá částice se pohybuje v magnetickém poli podél šroubovice, jehož osa je rovnoběžná s magnetickým polem. Projekce dráhy na rovině yz (při pohledu podél osy x) je kružnice. Jeho projekce na rovinách xy a xz jsou sinusoidy! Rovnice pohybu zůstanou stejné jako v kruhové dráze, za předpokladu, že v je nahrazeno v _⊥ = √ (ν _y ² + ν _z ² ).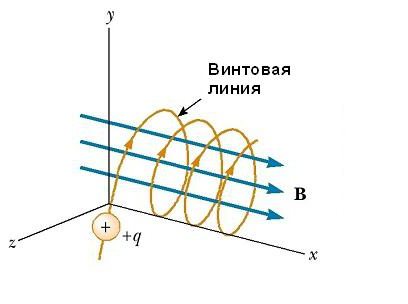

Nehomogenní magnetické pole: jak se v něm pohybují částice

Pohyb nabité částice v magnetickém poli, který je nehomogenní, nastává po složitých trajektoriích. Takže v poli, jehož velikost je zesílena na okrajích jejího regionu existence a oslabena ve svém středu, jak je například ukázáno na obrázku níže, může se částice oscilovat sem a tam mezi koncovými body. 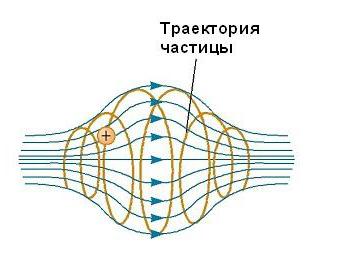Nabitá částice začíná na jednom konci šroubovice, vinutá podél síly a pohybuje se podél ní, dokud nedosáhne druhého konce, kde se otočí zpět. Tato konfigurace je známá jako "magnetická lahev", protože v ní mohou být zachyceny nabité částice. Byl použit k omezení plazmatu, plynu složeného z iontů a elektronů. Takový systém plazmového omezení může hrát klíčovou roli v řízení jaderné fúze, proces, který nám představuje téměř nekonečný zdroj energie. Bohužel má "magnetické láhve" své vlastní problémy. Pokud dojde k zachycení velkého počtu částic, srážky mezi nimi způsobí jejich únik ze systému.

Jak Země ovlivňuje pohyb kosmických částic

Válečné pásy Van Allena se skládají z nabitých částic (zejména elektronů a protonů) obklopujících Zemi ve formě toroidních oblastí (viz obrázek níže). Pohyb nabitých částic v magnetickém poli Země se vyskytuje ve spirále kolem linií síly od pólu k pólu, pokrývající tuto vzdálenost za několik vteřin. Tyto částice pocházejí převážně ze Slunce, ale některé pocházejí z hvězd a jiných nebeských předmětů. Z tohoto důvodu se nazývají kosmické paprsky. Většina z nich se odchyluje Zemské magnetické pole a nikdy nedosáhne atmosféry. Některé částice však spadají do pasti, to jsou ty, které tvoří pás Van Allen. Když jsou nad tyčemi, někdy se srazí s atomy v atmosféře, v důsledku čehož vyzařují viditelné světlo. Takže v severní a jižní polokouli jsou nádherné polární záře. Mají tendenci se vyskytovat v polárních oblastech, protože zde jsou pásy Van Allenu umístěny nejblíže k povrchu Země.

Někdy, nicméně, sluneční aktivita způsobuje větší počet nabitých částic vstupujících do těchto pásů a významně deformuje normální silu magnetického pole spojeného se Zemí. V těchto situacích může být aurora někdy vidět v nižších zeměpisných šířkách.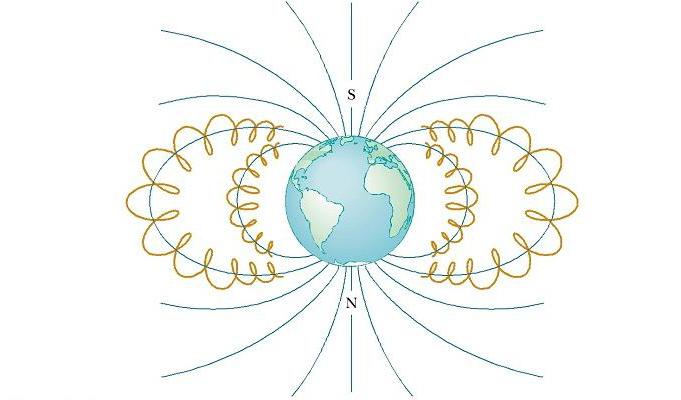

Volič rychlosti

V mnoha experimentech, při kterých dochází k pohybu nabitých částic v jednotném magnetickém poli, je důležité, aby se všechny částice pohybovaly téměř stejnou rychlostí. Toho lze dosáhnout použitím kombinace elektrického pole a magnetického pole, orientovaného tak, jak je znázorněno na obrázku níže. Homogenní elektrické pole je směrováno vertikálně dolů (v rovině stránky) a stejné magnetické pole je aplikováno ve směru kolmém na elektrický směr (na stránku). 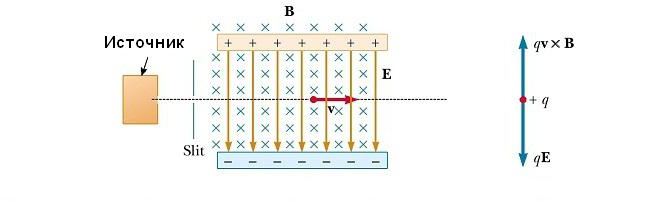Pro pozitivní q je magnetická síla F _B = qv x B směrována nahoru a elektrická síla qE je dolů. Když jsou hodnoty dvou polí zvoleny tak, že qE = qvB, částic se přesune do rovinné vodorovné čáry přes oblast pole. Z výrazu qE = qvB zjistíme, že pouze částice s rychlostí v = E / B procházejí bez odchylky vzájemně kolmými elektrickými a magnetickými poli. Síla F _B působící na částice pohybující se rychlostí větší než v = E / B se ukáže být více elektrická a jsou odkloněny nahoru. Ti z nich, kteří se pohybují s nižší rychlostí, se odchylují dolů.

Hmotnostní spektrometr

Toto zařízení odděluje ionty podle poměru jejich hmotnosti k náboji. Podle jedné verze tohoto zařízení, známého jako hmotnostní spektrometr Bainbridge, iontový paprsek nejprve prochází přes volič rychlosti a pak vstupuje do druhého pole B0, které je také homogenní a má stejný směr jako pole v selektoru (viz obrázek níže) . Po jeho vniknutí se pohyb nabité částice v magnetickém poli v polkruhu o poloměru r před nárazem do fotografické desky R. Pokud jsou ionty kladně nabité, paprsek vychýlí směrem nahoru, jak je znázorněno na obrázku. Pokud jsou ionty záporně nabité, paprsek se bude odvíjet směrem dolů. Z výrazu pro poloměr kruhové trajektorie částice můžeme najít poměr m / q

a pak pomocí rovnice v = E / B to zjistíme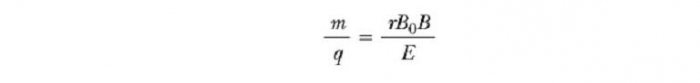

Můžeme tedy stanovit m / q měřením poloměru zakřivení, znalostí polí B, B ₀ a E. V praxi to obvykle měří hmotnost různých izotopů daného iontu, protože všichni nesou jeden náboj q. Tudíž hmotnostní poměr může být stanoven, i když q není známo. Variant této metody použil J. J. Thomson (1856-1940) v roce 1897 k měření poměru e / m _e pro elektrony.

Cyclotron

Může zrychlit nabité částice na velmi vysoké rychlosti. Obzvlášť důležité jsou zde elektrické a magnetické síly. Výsledné částečky s vysokou energií se používají k bombardování atomových jader, a tím k vytváření jaderných reakcí, které jsou zajímavé pro vědce. Řada nemocnic využívá vybavení cyklotronu pro výrobu radioaktivních látek pro diagnostiku a léčbu.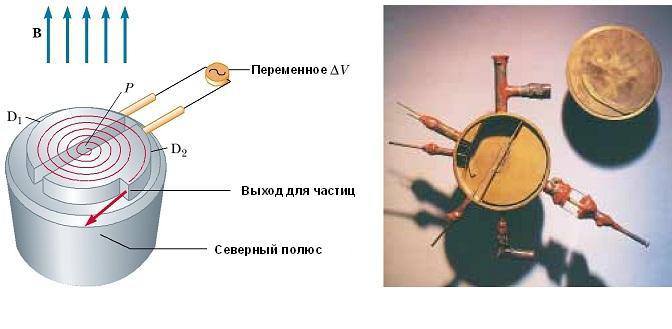

Schematické znázornění cyklotronu je znázorněno na obr. níže. Částice se pohybují uvnitř dvou polovičních válců D 1 a D 2, nazývaných deants. Vysokofrekvenční variabilní rozdíl potenciálu se aplikuje na dees oddělené mezerou a jednotné magnetické pole je směrováno podél osy cyklotronu (na obrázku není znázorněn jižní pól jeho zdroje).

Pozitivní iont uvolněný ze zdroje v bodě P v blízkosti středu zařízení v prvním duálním pohybu po polokruhovité trajektorii (znázorněn tečkovanou červenou čárou na obrázku) a přichází zpět do slotu v čase T / 2, kde T je doba jedné úplné otáčky uvnitř dvou duantů .

Frekvence aplikovaného potenciálního rozdílu je regulována tak, že polarity diante jsou obráceny v okamžiku, kdy iont vystupuje z jednoho dianthu. Pokud je použitý diferenciál potenciálu nastaven tak, že v tomto okamžiku D2 dostane nižší elektrický potenciál než D ₁ o qΔV, pak je iont zrychlen v mezeře před vstupem D ₂ a jeho kinetická energie se zvýší o qΔV. Pak se pohybuje okolo D ₂ podél polokruhově trajektorie většího poloměru (protože jeho rychlost se zvětšila).

Po nějaké době T / 2 opět vstoupí do mezery mezi deanty. V tomto okamžiku se polarita duentů opět změní a dalšímu "ránu" se dostane iont přes mezeru. Pohyb nabité částice v magnetickém poli ve spirále pokračuje, takže s každým průchodem jednoho duantu ion dostane další kinetickou energii rovnou qΔV. Když se poloměr jeho trajektorie přiblíží k poloměru dees, opouští iont systém přes výstupní štěrbinu. Je důležité poznamenat, že práce cyklotronu je založena na skutečnosti, že T nezávisí na rychlosti iontů a poloměru kruhové trajektorie. Můžeme se vyjádřit kinetické energie ionu, když opouští cyklotron, v závislosti na poloměru R v dělích. Víme, že rychlost kruhového pohybu částice je ν = qBR / m. Proto je jeho kinetická energie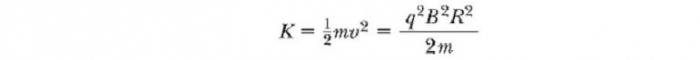

Když iontová energie v cyklotronu přesáhne přibližně 20 MeV, vstupují do hry relativistické účinky. Poznamenáváme, že T se zvyšuje a že pohybující se ionty nezůstanou ve fázi s aplikovaným potenciálním rozdílem. Některé urychlovače řeší tento problém změnou doby aplikovaného potenciálního rozdílu, takže zůstává ve fázi s pohyblivými ionty.

Hallův efekt

Když je vodič s proudem umístěn v magnetickém poli, vzniká další potenciální rozdíl ve směru kolmém ke směru proudu a magnetického pole. Tento jev, poprvé pozorovaný Edwin Hall (1855-1938) v roce 1879, je známý jako Hall. Je to vždy pozorováno, když se nabitá částice pohybuje v magnetickém poli. To vede k odklonu nosičů náboje na jedné straně vodiče v důsledku magnetické síly, kterou zažívají. Hallův efekt poskytuje informace o značce nosičů náboje a jejich hustotě, lze je také použít k měření velikosti magnetických polí.

Zařízení pro pozorování Hallova efektu se skládá z plochého vodiče s proudem I ve směru x, jak je znázorněno na obrázku níže. 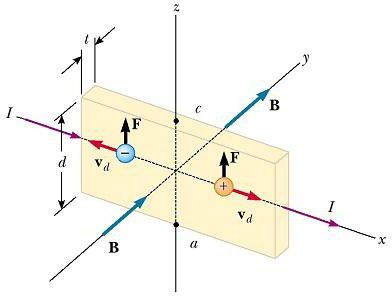Homogenní pole B se aplikuje ve směru y. Jsou-li nosiče náboje elektrony pohybující se podél osy x s driftovou rychlostí v _d , pak se projevují směrem vzhůru (s ohledem na negativní q) magnetická síla FB = qv _d x B, jsou vychylovány nahoru a hromadí se na horním okraji plochého vodiče, což vede k na dolním okraji se objevuje přebytek kladného náboje. Tato akumulace náboje na okrajích se zvyšuje, dokud elektrická síla vyplývající ze separace náboje nevyvažuje magnetickou sílu působící na nosiče. Když se tato rovnováha dosáhne, elektrony už nebudou vychylovat vzhůru. Citlivý voltmetr nebo potenciometr připojený k hornímu a spodnímu okraji vodiče může měřit potenciální rozdíl známý jako napětí Hall.